Tính Thể Tích Của Khối Tròn Xoay được Tạo Thành Khi Quay Hình Phẳng ...

Có thể bạn quan tâm

KHỞI ĐỘNG CHO MÙA THI ĐẠI HỌC 2026

Ôn đúng trọng tâm – Học chắc từ hôm nay

BẮT ĐẦU NGAY

Tính thể tích của khối tròn xoay được tạo thành khi quay hình phẳng (H) (phần tô đen trong hình bên)

Câu hỏi

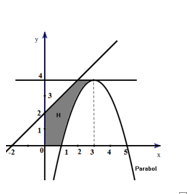
Nhận biết

Tính thể tích của khối tròn xoay được tạo thành khi quay hình phẳng (H) (phần tô đen trong hình bên) quanh trục Ox.

A. \(\dfrac{{61\pi }}{{15}}\). B. \(\dfrac{{88\pi }}{5}\) C. \(\dfrac{{8\pi }}{5}\). D. \(\dfrac{{424\pi }}{{15}}\).

Đáp án đúng: B

Lời giải của Tự Học 365

Giải chi tiết:

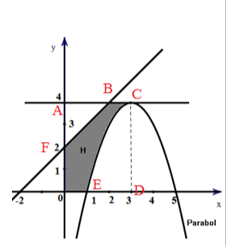
Thể tích cần tìm : \(V = {V_1} - {V_2} - {V_3}\)

Trong đó:

+) \({V_1}\) là thể tích khối tròn xoay tạo được khi quay hình chữ nhật ACDO quanh trục hoành, chính là thể tích khối trụ có chiều cao OD = 3, bán kính đáy OA = 4. Khi đó, \({V_1} = \pi {.3.4^2} = 48\pi \).

+) \({V_2}\) là thể tích khối tròn xoay tạo được khi quay tam giác ABF quanh trục hoành, ta có \(B(2;4)\).

\({V_2} = \pi {.4^2}.2 - \pi \int\limits_0^2 {{{\left( {x + 2} \right)}^2}dx} = 32\pi - {{56} \over 3}\pi = {{40} \over 3}\pi \)

+) \({V_3}\) là thể tích khối tròn xoay tạo được khi quay parabol “ECD” quanh trục hoành

\(\begin{array}{l}{V_3} = \pi \int\limits_1^3 {{{\left( { - {x^2} + 6x - 5} \right)}^2}dx} \\\,\,\,\,\, = \pi \int\limits_1^3 {\left( {{x^4} + 36{x^2} + 25 - 12{x^3} + 10{x^2} - 60x} \right)dx} \\\,\,\,\,\, = \pi \int\limits_1^3 {\left( {{x^4} + 46{x^2} + 25 - 12{x^3} - 60x} \right)dx} \\\,\,\,\,\, = \pi \left. {\left( {\dfrac{1}{5}{x^5} + \dfrac{{46}}{3}{x^3} + 25x - 3{x^4} - 30{x^2}} \right)} \right|_1^3\\\,\,\,\,\, = \left( {\dfrac{{123}}{5} - \dfrac{{113}}{{15}}} \right)\pi = \dfrac{{256}}{{15}}\pi \\ \Rightarrow V = {V_1} - {V_2} - {V_3} = \dfrac{{88\pi }}{5}\end{array}\).

Chọn: B

Ý kiến của bạn Hủy

Luyện tập

Phòng tự luyện, thi thử
Khóa học, tài liệu
Cách tự học

Câu hỏi liên quan

Câu 2: Đề thi thử THPT Hà Trung - Thanh Hóa

Chi tiết
Giải phương trình: (sin2x + cos2x)cosx + 2cos2x - sinx = 0
Chi tiết
câu 2

Chi tiết
Giải phương trình (1 – i)z + (2 – i) = 4 – 5i trên tập số phức.
Chi tiết
Giải phương trình 31 – x – 3x + 2 = 0.
Chi tiết
câu 7

Chi tiết
Tìm số nguyên dương n nhỏ nhất sao cho z1 = là số thực và z2 = là số ảo.
Chi tiết
Giải phương trình 72x + 1 – 8.7x + 1 = 0.
Chi tiết
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d: = = và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
Chi tiết
Giải phương trình : z3 + i = 0
Chi tiết