Tính Tích Phân Bằng Phương Pháp Đổi Biến Số Và Bài Tập Có Lời Giải
Có thể bạn quan tâm
Vậy phương pháp tính tích phân bằng cách đổi biến số thực hiện như thế nào? Bài viết dưới đây chúng ta cùng tìm hiểu các bước thực hiện khi tính tích phân bằng phương pháp đổi biến số và vận dụng giải các bài tập tích phân minh họa.
» Đừng bỏ lỡ: Tích phân từng phần, Công thức cách tính và Bài tập có lời giải chi tiết, dễ hiểu
I. Tính tích phân bằng phương pháp đổi biến số
• Kiến thức cần nhớ:
Định lý: Cho hàm số f(x) liên tục trên [a;b]. Giả sử hàm số x = μ(t) có đạo hàm liên tục trên [α;β] sao cho μ(α) = a; μ(β) = b và a ≤ μ(t) ≤ b với mọi t ∈ [α;β]. Khi đó:
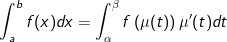
- Khi tính tích phân bằng phương pháp đổi biến số ta thường gặp 2 dạng đổi biến sau:
• Phương pháp đổi biến số dạng 1:
- Đặt 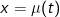 thỏa điều kiện của công thức
thỏa điều kiện của công thức
- Biến đổi: ![f(x)dx=f\left [ \mu (t) \right ] \mu' (t)dt=g(t)dt](https://hayhochoi.vn/uploads/news/wyswyg/2020_12/1608695343y44oj45wyk_1608696454.gif)
- Tìm một nguyên hàm của g(t) rồi áp dụng
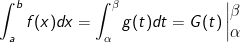
> Lưu ý: Đối với dạng (a2 - x2) thì đặt x = asint, dạng (a2 + x2) thì đặt x = atant.
• Phương pháp đổi biến số dạng 2:
- Đặt 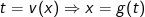 đổi cận
đổi cận
- Biểu diễn f(x)dx = g(t)dt
- Áp dụng: 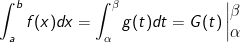
II. Bài tập tính tích phân bằng phương pháp đổi biến số
* Bài tập 1 : Tính cáctích phân sau:
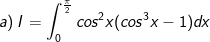
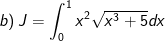
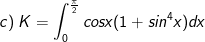
* Lời giải: (sử dụng phương pháp đổi biến số dạng 1)
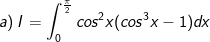
- Ta có: 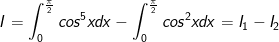
- Xét: 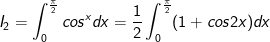
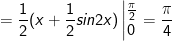
- Xét: 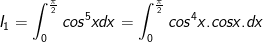
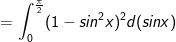
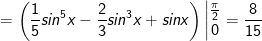
Vậy: 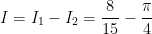
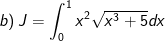
- Ta có: 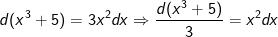
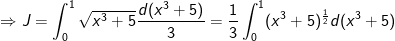
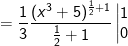
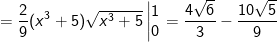
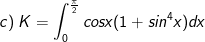
- Ta có: 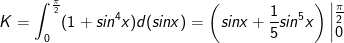
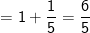
* Bài tập 2: Tính các tính phân sau:
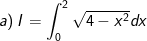
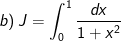
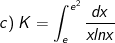
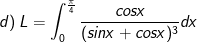
* Lời giải: (sử dụng phương pháp đổi biến số dạng 2)
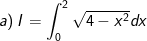
- Đặt ![x=2sint,\: t\in \left [ -\frac{\pi }{2};\frac{\pi }{2} \right ]](https://hayhochoi.vn/uploads/news/wyswyg/2020_12/1608632426lyd2fs2srk_1608695351_1608696466.gif)
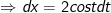
- Đổi cận: 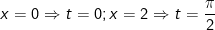
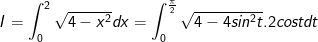
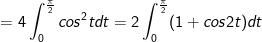
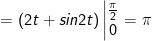
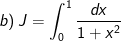
- Đặt 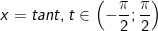
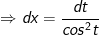
- Đổi cận: x = 0 thì t = 0; x = 1 thì t = π/4.
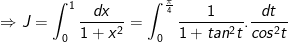
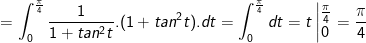
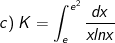
- Đặt 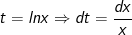
- Đổi cận: x = e ⇒ t = 1; x = e2 ⇒ t = 2.
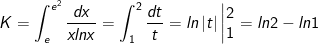
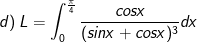
- Ta có: 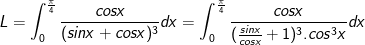
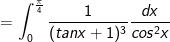
- Đặt 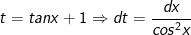
- Đổi cận: x = 0 ⇒ t = 1; x = π/4 ⇒ t = 2.
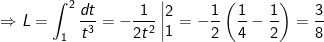
III. Bài tập tính tích phân bằng phương pháp đổi biến số tự làm
* Bài tập 1: Tính các tính phân sau:
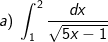
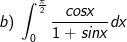
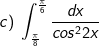
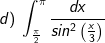
* Hướng dẫn:
a) Đặt t = 5x - 1 (hoặc sử dụng pp đổi biến số dạng 1)
b) Đặt t = 1 + sinx
c) Đặt t = 2x.
d) Đặt t = x/3.
* Bài tập 2: Tính các tính phân sau:
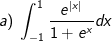
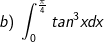
* Hướng dẫn:
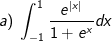
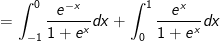
Xét 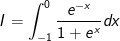 Đặt t = -x thì dt = -dx hay dx = -dt;
Đặt t = -x thì dt = -dx hay dx = -dt;
Đổi cận: x = -1 thì t = 1; x = 0 thì t = 0.
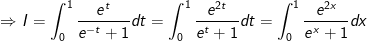
Do đó: 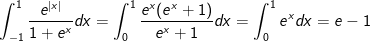
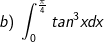
- Ta có: ![\int_{0}^{\frac{\pi }{4}}tan^3xdx=\int_{0}^{\frac{\pi }{4}}[tanx(1 + tan^2x)-tanx]dx](https://hayhochoi.vn/uploads/news/wyswyg/2020_12/1608695424dr5pbupzzt_1608696479.gif)
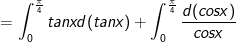
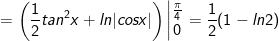
* Bài tập 3: Tính các tích phân sau:
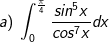
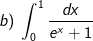
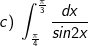
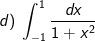
* Hướng dẫn:
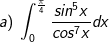
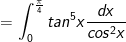
- Đặt t = tanx.
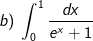
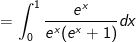
- Đặt t = ex + 1.
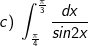
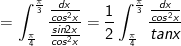
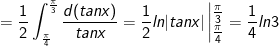
d) Đặt x = tant.
* Bài tập 4. Tính các tích phân sau:
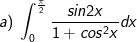
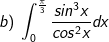
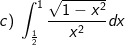
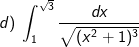
* Hướng dẫn:
a) Đặt t = 1 + cos2x.
c) Đặt x = sint
d) Đặt x = tant.
¤ Một số dấu hiệu nhận biết các tích phân có thể dùng phương pháp đổi biến số.
+ Có 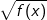 có thể đặt
có thể đặt 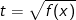
+ Có 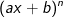 có thể đặt
có thể đặt 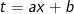
+ Có 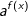 có thể đặt
có thể đặt 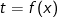
+ Có 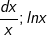 có thể đặt t = lnx (hoặc biểu thức chứa lnx).
có thể đặt t = lnx (hoặc biểu thức chứa lnx).
+ Có ex có thể đặt t = ex (hoặc biểu thức chứa ex)
+ Có cosx (hoặc sinx) có thể đặt t = sinx (hoặc t = cosx)
+ Có 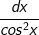 (hoặc
(hoặc 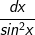 ) có thể đặt t = tanx (hoặ t = cotx).
) có thể đặt t = tanx (hoặ t = cotx).
Từ khóa » Nguyên Hàm đặt X=tant
-
Bài Tập Tìm Nguyên Hàm Bằng Cách đổi Biến Số (Đặt X = Hàm Theo ...
-
Nếu đặt X = Tan T Thì Nguyên Hàm I = Int Dx Căn 1 + X^2 Bằng
-
Phương Pháp đặt ẩn Phụ Trong Tính Tích Phân - 123doc
-
Phương Pháp đổi Biến Số Trong Nguyên Hàm Và Tích Phân
-
Tính Nguyên Hàm Bằng Phương Pháp đổi Biến Số - Mathsilo
-
Công Thức Nguyên Hàm, Bảng Nguyên Hàm đầy đủ & Mở Rộng
-
Nếu đặt X=sint Thì Nguyên Hàm X^2 Căn Bậc Hai Của 1-x^2 Dx
-
Tính Tích Phân Bằng Phương Pháp Đổi Biến Số Và Bài Tập Có Lời Giải
-
Toán Học - Các Công Thức Nguyên Hàm Mở Rộng - Thư Viện Đề Thi
-
Cách Tính Nguyên Hàm Tanx Và Bài Tập Áp Dụng - Marathon
-
Toán 12 - đặt X= Tant => Dx - HOCMAI Forum
-
Sử Dụng Phép đặt $x = \tan T$, Tìm Biểu Diễn Của Nguyên Hàm $\int ...
-
[] - Phương Pháp Tính Tích Phân đổi Biến Dạng Lượng Giác Hoá