Tính Tổng Các Nghiệm Nguyên Của Bất Phương Trình (log _2^2x - Left ...

Tính tổng các nghiệm nguyên của bất phương trình \(\log _2^2x – \left( {x + 2} \right)\log x + 3\left( {x – 1} \right) > 0\). A.\(36\).

B. \(33\).

C. \(25\).

D. \(45\).

Lời giải chi tiết

PHÁT TRIỂN TƯƠNG TỰ CÂU 47 ĐỀ TOÁN THAM KHẢO 2021 CỦA BỘ. BIÊN SOẠN TỪ STRONG TEAM TOÁN VDC – BIÊN TẬP WEB BOOKTOAN.COM

PHƯƠNG PHÁP CHUNG 1. ĐẠO HÀM g'(x) 2. DÙNG HÀM ĐẶC TRƯNG, BIẾN ĐỔI MŨ, LOGARIT ĐỂ CÔ LẬP m = g'(x) 3. Lập BBT xét dấu g'(x) 4. Dựa vào BBT xét các điều kiện thoat yêu cầu bài toán.

Điều kiện của bất phương trình : \(x > 0\) \(\log _2^2x – \left( {x + 2} \right){\log _2}x + 3\left( {x – 1} \right) > 0\) (*) \( \Leftrightarrow \log _2^2x – \left( {x – 1} \right){\log _2}x – 3{\log _2}x + 3\left( {x – 1} \right) > 0\) \( \Leftrightarrow {\log _2}x.\left[ {{{\log }_2}x – \left( {x – 1} \right)} \right] – 3\left[ {{{\log }_2}x – \left( {x – 1} \right)} \right] > 0\) \( \Leftrightarrow \left( {{{\log }_2}x – 3} \right).\left[ {{{\log }_2}x – \left( {x – 1} \right)} \right] > 0\). + Xét hàm số \(f\left( x \right) = {\log _2}x – \left( {x – 1} \right)\) có \(f’\left( x \right) = \frac{1}{{x.\ln 2}} – 1\); \(f’\left( x \right) = 0 \Leftrightarrow x = \frac{1}{{\ln 2}} \Leftrightarrow x = {\log _2}e\). Bảng biến thiên

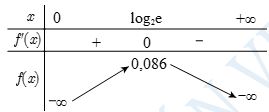
Từ BBT ta thấy phương trình \(f\left( x \right) = 0\) luôn có 2 nghiệm phân biệt. Mặt khác \(f\left( 1 \right) = f\left( 2 \right) = 0\). Suy ra \({\log _2}x – \left( {x – 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 2\end{array} \right.\) Kẻ trục xét dấu \(g\left( x \right) = \left( {{{\log }_2}x – 3} \right).\left[ {{{\log }_2}x – \left( {x – 1} \right)} \right]\)

Suy ra tập nghiệm của bất phương trình là \(S = \left( {0\,;\,1} \right) \cup \left( {2\,;\,8} \right)\) Vậy tập các nghiệm nguyên của bất phương trình (*) là \(T = \left\{ {3\,,\,4\,,\,5\,,\,6\,,\,7} \right\}\) Tổng các nghiệm nguyên của bất phương trình là \(3 + 4 + 5 + 6 + 7 = 25\).