Toán 10 - Cung Và Góc Lượng Giác - Lý Thuyết Và Giải Bài Tập SGK

5/5 - (4 bình chọn)

Hôm nay, toppy.vn sẽ ôn tập lại cho các bạn những kiến thức cơ bản về cung và góc lượng giác. Và luyện tập một số bài tập SGK, hướng dẫn giải chi tiết tường bài. Cùng toppy luyện tập lại ngay kiến thức cơ bản về toán 10 Cung và góc lượng giác nhé!

Table of Contents

Toggle

• Kiến thức cơ bản cần nắm
• Cơ sở lý thuyết về cung và góc lượng giác
  • Khái niệm về đơn vị đo góc và cung tròn
  • Thế nào là góc? Thế nào là cung lượng giác?
  • Định lý về hệ thức Salo
  • Hướng dẫn vẽ cung lượng giác trên đường tròn lượng giác
• Bài tập cung và góc lượng giác – Các bài tập SGK
• Một số bài tập làm thêm 
• Tổng kết kiến thức về toán 10 Cung và góc lượng giác

Kiến thức cơ bản cần nắm

• Nắm rõ được các khái niệm cơ bản về cung và góc lượng giác.
• Biểu diễn được cung lượng giác ở trên các đường tròn lượng giác.
• Luyện tập thành thạo các bài toán về dạng bài này.

Cơ sở lý thuyết về cung và góc lượng giác

Khái niệm về đơn vị đo góc và cung tròn

Thế nào là góc? Thế nào là cung lượng giác?

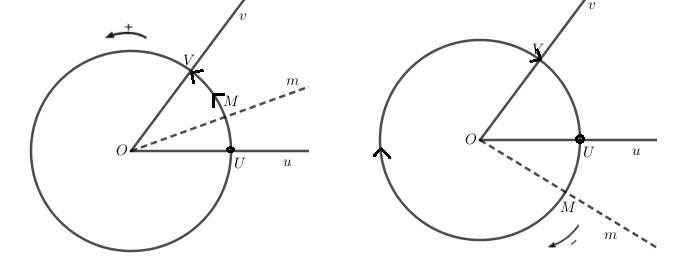
Định lý về hệ thức Salo

Cho 3 tia chung gốc O là OA, OB và OC bất kỳ. Ta có:

Hướng dẫn vẽ cung lượng giác trên đường tròn lượng giác

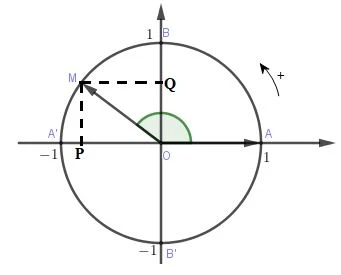
>> Xem thêm: Vị trí tương đối của đường thẳng và đường tròn – Học hình toán 9

Bài tập cung và góc lượng giác – Các bài tập SGK

Bài 1: SGK – 140

Giải:

Khi các điểm đầu của các cung trùng nhau và có số đo 2 cung lệch nhau là kπ2 hay k3600, k ∈ Ζ. Thì ta có thể xác định các điểm cuối có thể trùng nhau.

Ví dụ ta có 2 cung có các số đo góc lần lượt là 300 và 300 + 3600 = 3900 có điểm cuối trùng nhau hoặc có các số đo góc π/6, π/6 + 2, π/6 – 2 có điểm cuối là trùng nhau.

Bài 2: SGK-140 

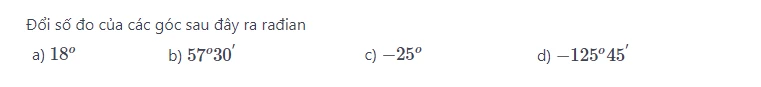
Áp dụng công thức quy đổi sang radian sau: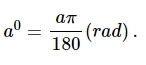

Giải:

a) Ta có: 180 = 18π/180 = π/10 (rad)

b) Ta có: 

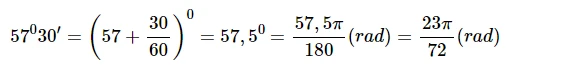
c)

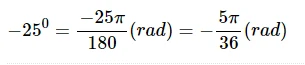
d) Ta có:

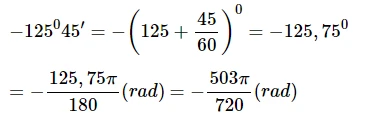
Bài 3: SGK – 140

Hướng dẫn giải bài toán:

Hãy sử dụng mối quan hệ giữa độ và radian để giải quyết bài toán: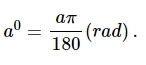

Bài 4: SGK – 140

a) Sử dụng công thức độ dài của cung tròn góc α(rad) là l = R với R là bán kính của đường tròn đó.

Ta có: l = Rα= 20.π/15 ≈ 4,19 cm 

b) l = Rα = 20.1,5 = 30cm

c) Trước khi tính độ dài của các cung. Ta đổi đơn vị độ sang radian theo công thức

Ta có: 370 = 37π/ 180

=> l = 20. 37π/ 180 ≈ 12,92 cm

Bài 5: SGK – 140

Giải bài toán:

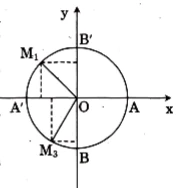
Ghi nhớ: 

• Biểu diễn cung lượng giác trên các đường tròn lượng giác. Ta chọn gốc tọa độ A (1;0) để làm điểm đầu cho tất cả các cung lượng giác trên đường tròn lượng giác. Tiếp đến ta biểu diễn các cung lượng đó theo số đo α trên đường tròn lượng giác. Ta chọn điểm M được xác định bởi hệ thức sau: sđ góc AM = α.
• Trên đường tròn lượng giác, chiều dương là chiều ngược của kim đồng hồ. Còn chiều âm là chiều thuận của kim đồng hồ.

Bài 6: SGK – 140

Giải bài toán

a)

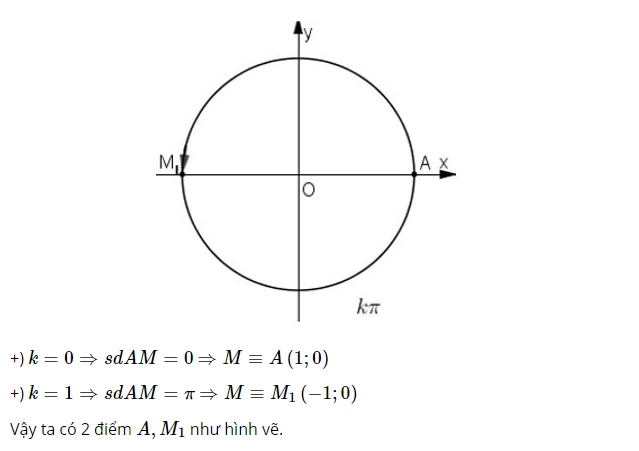
b)

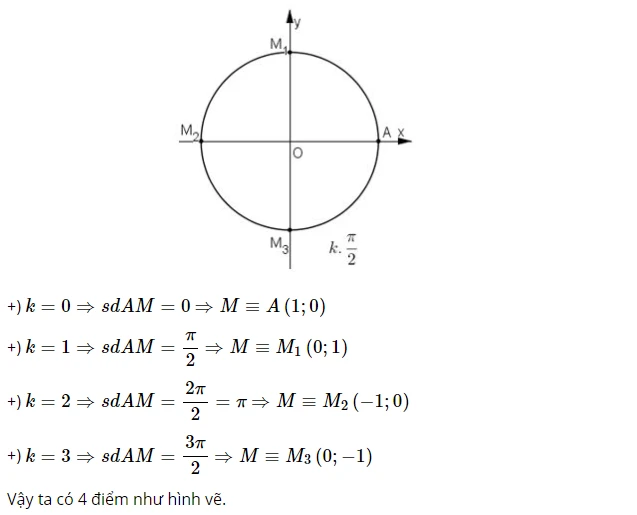
c)

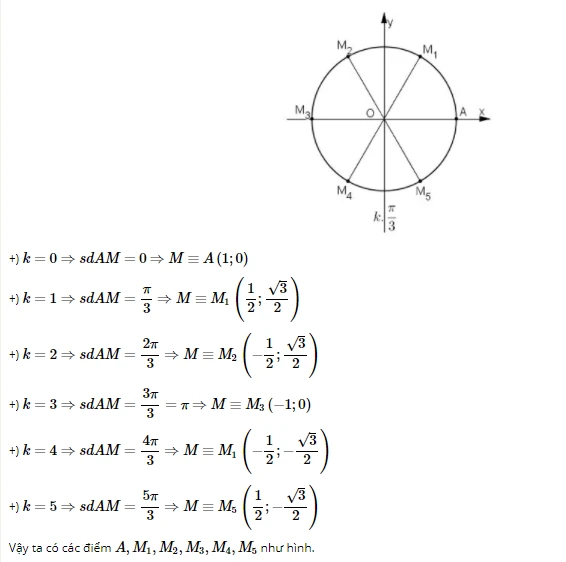
Bài 7: SGK – 140

Giải bài toán:

Các điểm đối xứng nhau qua gốc O có các số đo các cung tương ứng hơn kém nhau π. Ta có hình vẽ:

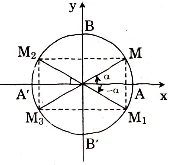
Ta có:

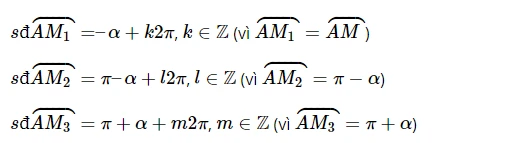
Một số bài tập làm thêm 

Dạng 1: Mối quan hệ và liên hệ giữa độ và radian

Bài 1: Vận dụng kiến thức đã học hãy quy đổi số đo của các góc sau từ độ ra radian

a) 540

b) 30045’

c) -500

d) -20035’

Bài 2: Đổi các số đo của các góc sau ra độ

a) π/2

b) 2π/ 3

c) 5π/ 2

d) 4,5π

Dạng 2: Độ dài của các cung lượng giác

Bài 1: Cho một đường tròn có bán kính là 26m. Hãy xác định độ dài của cung trên các đường tròn đó theo số đo của các góc sau:

a) 2π/ 5

b) 250

c) ¾

Bài 2: Một hải lý có độ dài cung tròn xích đạo có số đo là (1/60)0 = 1’. Biết độ dài của xích đạo là 50.000 km. Vậy một hải lý sẽ có chiều dài là bao nhiêu km?

Bài 3: Bánh xe của một người đi xe đạp được quay là 20 vòng trong 10s.

1. Hãy tính góc mà bánh xe đạp quay được trong 2s theo độ và radian.
2. Hãy tính quãng đường mà người đi xe đạp đó đi được trong 1p, biết rằng đường kính của bánh xe đạp đó 720mm.

Dạng 3: Biểu diễn – vẽ cung lượng giác trên đường tròn lượng giác.

Bài 1: Cho cung lượng giác có số đo x = π/ 4 + kπ với k là số nguyên bất kỳ. Hỏi có bao nhiêu giá trị k thỏa mãn được điều kiện x ∈ [2π; 7π]?

Bài 2: Hãy biểu diễn cung lượng giác có số đo x = k2π/ 3 với k là một số nguyên bất kỳ.

Bài 3: Biểu diễn cung lượng giác có số đo là x = -6250.

Hãy vận dụng những lý thuyết được ôn tập ở trên và giải ngay các bài tập dưới đây để có thể thành thạo, luyện tập kỹ năng về phần cung và góc lượng giác.

Bài 4: Khi biểu diễn các cung lượng giác có các số đo lần lượt là x = kπ/2 và y = k2π trên đường tròn lượng giác. Vậy số điểm chung sẽ nhận được là bao nhiêu?

Bài 5: Hãy tìm tất cả các điểm có trên đường tròn lượng giác và hãy biểu diễn các cung lượng giác với số đo là x = kπ/2 không trùng với điểm biểu diễn của cung lượng giác nào có số đo y = k2π.

Tổng kết kiến thức về toán 10 Cung và góc lượng giác

Trên đây là toàn bộ kiến thức lý thuyết cơ bản về cung và góc lượng giác. Hy vọng những chia sẻ trên cùng một số bài tập làm thêm có thể giúp các bạn có thể luyện tập thành thạo, xử lý mọi bài tập liên quan đến toán 10 cung và góc lượng giác. Toppy.vn chúc các bạn luôn thành công trên con đường học tập của mình.

Xem thêm: 

• Đường tròn ngoại tiếp đường tròn nội tiếp
• Liên hệ giữa cung và dây – Lý thuyết cần nhớ cùng
• Vị trí tương đối của hai đường tròn