Toán 10 Ôn Tập Chương 2 Hàm Số Bậc Nhất Và Bậc Hai - HOC247
Có thể bạn quan tâm
Nội dung bài giảng sẽ giúp các em tổng hợp kiến thức về các hàm số đã được học gồmhàm số y=ax+b và hàm số bậc hai thông qua các sơ đồ. Bên cạnh đó các em còn được ôn lại phương pháp giải toán thông qua một số bài tập có hướng dẫn giải chi tiết.
ATNETWORK YOMEDIA1. Tóm tắt lý thuyết
1.1. Hàm số bậc nhất
1.2. Hàm số bậc hai
2. Bài tập minh hoạ
3. Luyện tập bài 4 chương 2 đại số 10
3.1. Trắc nghiệm về hàm số bậc nhất và hàm số bậc hai
3.2. Bài tập SGK & Nâng cao về hàm số bậc nhất và hàm số bậc hai
4. Hỏi đáp về bài 4 chương 2 đại số 10

Tóm tắt lý thuyết
1.1. Hàm số bậc nhất
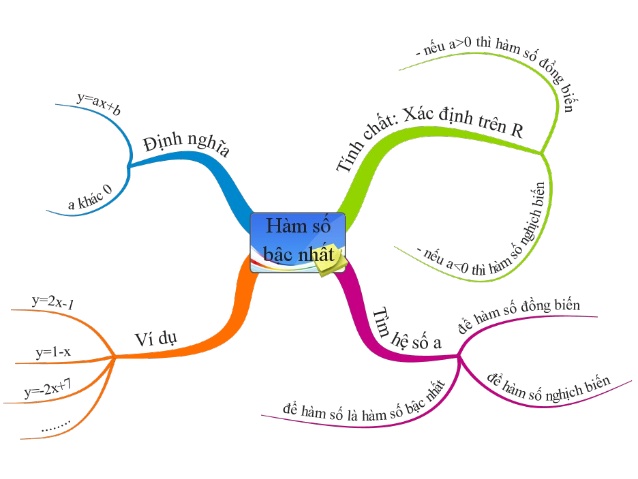
Sơ đồ tư duy hàm số bậc nhất
1.2. Hàm số bậc hai
Khảo sát sự biến thiên và vẽ đồ thị hàm số bậc hai
Bài tập minh họa
Ví dụ 1:
Cho các hàm số : \(y = - 2x + 3,\,\,y = x + 2,\,\,y = \frac{3}{2}\).
a) Vẽ đồ thị các hàm số trên.
b) Dựa vào đồ thị hãy xác định giao điểm của các đồ thị hàm số đó.
Hướng dẫn:
a) Đồ thị hàm số \(y = - 2x + 3\) đi qua \(A\left( {0;3} \right),\,\,B\left( {\frac{3}{2};0} \right)\)
Đồ thị hàm số \(y = x + 2\) đi qua \(A'\left( {0;2} \right),\,\,B'\left( { - 2;0} \right)\)
Đồ thị hàm số \(y = \frac{3}{2}\) đi qua \(M\left( {0;\frac{3}{2}} \right)\) và song song với trục hoành.
.png)
b) Giao điểm của hai đồ thị hàm số \(y = - 2x + 3,\,\,y = x + 2\) là \({M_1}\left( {\frac{1}{3};\frac{7}{3}} \right)\).
Giao điểm của hai đồ thị hàm số \(y = - 2x + 3,\,\,y = \frac{3}{2}\) là \({M_2}\left( {\frac{3}{4};\frac{3}{2}} \right)\).
Giao điểm của hai đồ thị hàm số \(\,y = x + 2,\,\,y = \frac{3}{2}\) là \({M_2}\left( { - \frac{1}{2};\frac{3}{2}} \right)\).
Ví dụ 2:
Vẽ đồ thị hàm số \(y = 2x - 3.\) Từ đó suy ra đồ thị của:
\(\left( {{C_1}} \right):y = 2\left| x \right| - 3,\) \(\left( {{C_2}} \right):y = \left| {2x - 3} \right|,\) \(\left( {{C_3}} \right):y = \left| {2\left| x \right| - 3} \right|\)
Hướng dẫn:
Đồ thị hàm số \(y = 2x - 3\) đi qua \(A\left( {0; - 3} \right),\,\,B\left( {2;1} \right)\) ta gọi là \(\left( C \right)\)
\(\bullet \) Khi đó đồ thị hàm số \(\left( {{C_1}} \right):y = 2\left| x \right| - 3\) là phần được xác định như sau
Ta giữ nguyên đồ thị \(\left( C \right)\) ở bên phải trục tung; lấy đối xứng đồ thị \(\left( C \right)\) ở phần bên phải trục tung qua trục tung.
\(\bullet \) \(\left( {{C_2}} \right):y = \left| {2x - 3} \right|\) là phần đồ thị \(\left( C \right)\) nằm phái trên trục hoành và đồ thị lấy đối xứng qua trục hoành của phần nằm trên trục hoành của \(\left( C \right)\).
\(\bullet \) \(\left( {{C_3}} \right):y = \left| {2\left| x \right| - 3} \right|\) là phần đồ thị \(\left( {{C_1}} \right)\) nằm phái trên trục hoành và đồ thị lấy đối xứng qua trục hoành của phần nằm trên trục hoành của \(\left( {{C_1}} \right)\).
Ví dụ 3:
Xác định phương trình của Parabol (P): \(y = {x^2} + bx + c\) trong các trường hợp sau:
a) (P) đi qua điểm \(A\left( {1;{\rm{ }}0} \right)\) và \(B\left( { - 2; - 6} \right)\).
b) (P) có đỉnh \(I\left( {1;{\rm{ }}4} \right)\).
c) (P) cắt trục tung tại điểm có tung độ bằng 3 và có đỉnh \(S\left( { - 2; - 1} \right)\).
Hướng dẫn:
a) Vì (P) đi qua A, B nên \(\left\{ \begin{array}{l}0 = 1 + b + c\\ - 6 = 4 - 2b + c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b + c = - 1\\2b - c = 10\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 3\\c = - 4\end{array} \right.\).
Vậy (P):\(y = {x^2} + 3x--4\) .
b) Vì (P) có đỉnh \(I\left( {1;{\rm{ }}4} \right)\) nên\(\left\{ \begin{array}{l}\frac{{ - b}}{2} = 1\\ - \frac{{{b^2} - 4c}}{4} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = - 2\\c = 5\end{array} \right.\).
Vậy (P):\(y = {\rm{ }}{x^2}--2x + 5\) .
c) (P) cắt Oy tại điểm có tung độ bằng 3 suy ra \(c = 3\)
(P) có đỉnh \(S\left( { - 2; - 1} \right)\)suy ra: \(\left\{ \begin{array}{l} - \frac{b}{{2a}} = - 2\\ - 1 = 4a - 2b + 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 4\\a = 1\end{array} \right.\)
Ví dụ 4:
Cho hàm số \(y = {x^2} - 6x + 8\)
a) Lập bảng biến thiên và vẽ đồ thị các hàm số trên.
b) Sử dụng đồ thị để biện luận theo tham số \(m\) số điểm chung của đường thẳng \(y = m\) và đồ thị hàm số trên.
c) Sử dụng đồ thị, hãy nêu các khoảng trên đó hàm số chỉ nhận giá trị dương.
d) Sử dụng đồ thị, hãy tìm giá trị lớn nhất, nhỏ nhất của hàm số đã cho trên \(\left[ { - 1;5} \right]\).
Hướng dẫn:
a) Ta có \( - \frac{b}{{2a}} = 3,\,\, - \frac{\Delta }{{4a}} = - 1\)
Bảng biến thiên:
Suy ra đồ thị hàm số \(y = {x^2} + 3x + 2\) có đỉnh là \(I\left( {3; - 1} \right)\), đi qua các điểm \(A\left( {2;0} \right),\,\,B\left( {4;0} \right)\)
Nhận đường thẳng x = 3\) làm trục đối xứng và hướng bề lõm lên trên.
.png)
b) Đường thẳng \(y = m\) song song hoặc trùng với trục hoành do đó dựa vào đồ thị ta có
Với \(m < - 1\) đường thẳng \(y = m\) và parabol \(y = {x^2} - 6x + 8\) không cắt nhau
Với \(m = - 1\) đường thẳng \(y = m\) và parabol \(y = {x^2} - 6x + 8\) cắt nhau tại một điểm(tiếp xúc)
Với \(m > - 1\) đường thẳng \(y = m\) và parabol \(y = {x^2} - 6x + 8\) cắt nhau tại hai điểm phân biệt
c) Hàm số nhận giá trị dương ứng với phần đồ thị nằm hoàn toàn trên trục hoành
Do đó hàm số chỉ nhận giá trị dương khi và chỉ khi \(x \in \left( { - \infty ;2} \right) \cup \left( {4; + \infty } \right)\).
d) Ta có \(y\left( { - 1} \right) = 15,\,\,y\left( 5 \right) = 13,\,\,y\left( 3 \right) = - 1\), kết hợp với đồ thị hàm số suy ra
\(\mathop {\max }\limits_{\left[ { - 1;5} \right]} y = 15\) khi và chỉ khi\(x = - 1\)
\(\mathop {\min }\limits_{\left[ { - 1;5} \right]} y = - 1\) khi và chỉ khi \(x = 3\)
3. Luyện tập Bài 4 chương 2 đại số 10
Nội dung bài giảng sẽ giúp các em tổng hợp kiến thức về các hàm số đã được học gồmhàm số y=ax+b và hàm số bậc hai thông qua các sơ đồ. Bên cạnh đó các em còn được ôn lại phương pháp giải toán thông qua một số bài tập có hướng dẫn giải chi tiết.
3.1 Trắc nghiệm về Hàm số bậc nhất và Bậc hai
Để cũng cố bài học xin mời các em cũng làm Bài kiểm tra Trắc nghiệm Toán 10 Ôn tập chương II để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.
-
Câu 1:
Cho đồ thị hàm số \(y = f\left( x \right)\) như hình vẽ:
.png)
Kết luận nào trong các kết luận sau là đúng:
- A. Đồng biến trên \(\mathbb{R}\)
- B. Hàm số chẵn.
- C. Hàm số lẻ
- D. Cả ba đáp án đếu sai
-
Câu 2:
Với những giá trị nào của m thì hàm số \(y = - {x^3} + 3\left( {{m^2} - 1} \right){x^2} + 3x\) là hàm số lẻ:
- A. \(m = 1\)
- B. \(m = - 1\)
- C. \(m = \pm 1\)
- D. một kết quả khác.
-
Câu 3:
Cho đồ thị hàm số \(y = ax + b\) như hình vẽ:
.png)
Khi đó giá trị a, b của hàm số trên là:
- A. \(a = 3;b = - 3\)
- B. \(a = - 1;b = 3\)
- C. \(a = 3;b = 3\)
- D. \(a = 1;b = - 3\)
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!
3.2 Bài tập SGK và Nâng Cao về Hàm số bậc nhất và Bậc hai
Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Toán 10 Ôn tập chương II sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK Đại số 10 Cơ bản và Nâng cao.
Bài tập 1 trang 50 SGK Đại số 10
Bài tập 2 trang 50 SGK Đại số 10
Bài tập 3 trang 50 SGK Đại số 10
Bài tập 4 trang 50 SGK Đại số 10
Bài tập 5 trang 50 SGK Đại số 10
Bài tập 6 trang 50 SGK Đại số 10
Bài tập 7 trang 50 SGK Đại số 10
Bài tập 8 trang 50 SGK Đại số 10
Bài tập 9 trang 50 SGK Đại số 10
Bài tập 10 trang 51 SGK Đại số 10
Bài tập 11 trang 51 SGK Đại số 10
Bài tập 12 trang 51 SGK Đại số 10
Bài tập 2.27 trang 42 SBT Toán 10
Bài tập 2.28 trang 42 SBT Toán 10
Bài tập 2.29 trang 43 SBT Toán 10
Bài tập 2.30 trang 43 SBT Toán 10
Bài tập 2.31 trang 43 SBT Toán 10
Bài tập 2.32 trang 43 SBT Toán 10
Bài tập 2.33 trang 43 SBT Toán 10
Bài tập 39 trang 63 SGK Toán 10 NC
Bài tập 40 trang 63 SGK Toán 10 NC
Bài tập 41 trang 63 SGK Toán 10 NC
Bài tập 42 trang 63 SGK Toán 10 NC
Bài tập 43 trang 63 SGK Toán 10 NC
Bài tập 44 trang 64 SGK Toán 10 NC
Bài tập 45 trang 64 SGK Toán 10 NC
Bài tập 46 trang 64 SGK Toán 10 NC
4. Hỏi đáp về bài 4 chương 2 đại số 10
Nếu có thắc mắc cần giải đáp các em có thể để lại câu hỏi trong phần Hỏi đáp, cộng đồng Toán HỌC247 sẽ sớm trả lời cho các em.
-- Mod Toán Học 10 HỌC247
 NONE
NONE Bài học cùng chương
 Toán 10 Bài 1: Hàm số
Toán 10 Bài 1: Hàm số  Toán 10 Bài 2: Hàm số y = ax + b
Toán 10 Bài 2: Hàm số y = ax + b  Toán 10 Bài 3: Hàm số bậc hai ADSENSE TRACNGHIEM
Toán 10 Bài 3: Hàm số bậc hai ADSENSE TRACNGHIEM  Bộ đề thi nổi bật
Bộ đề thi nổi bật  UREKA AANETWORK
UREKA AANETWORK 
XEM NHANH CHƯƠNG TRÌNH LỚP 10
Toán 10
Toán 10 Kết Nối Tri Thức
Toán 10 Chân Trời Sáng Tạo
Toán 10 Cánh Diều
Giải bài tập Toán 10 Kết Nối Tri Thức
Giải bài tập Toán 10 CTST
Giải bài tập Toán 10 Cánh Diều
Trắc nghiệm Toán 10
Ngữ văn 10
Ngữ Văn 10 Kết Nối Tri Thức
Ngữ Văn 10 Chân Trời Sáng Tạo
Ngữ Văn 10 Cánh Diều
Soạn Văn 10 Kết Nối Tri Thức
Soạn Văn 10 Chân Trời Sáng tạo
Soạn Văn 10 Cánh Diều
Văn mẫu 10
Tiếng Anh 10
Giải Tiếng Anh 10 Kết Nối Tri Thức
Giải Tiếng Anh 10 CTST
Giải Tiếng Anh 10 Cánh Diều
Trắc nghiệm Tiếng Anh 10 KNTT
Trắc nghiệm Tiếng Anh 10 CTST
Trắc nghiệm Tiếng Anh 10 CD
Giải Sách bài tập Tiếng Anh 10
Vật lý 10
Vật lý 10 Kết Nối Tri Thức
Vật lý 10 Chân Trời Sáng Tạo
Vật lý 10 Cánh Diều
Giải bài tập Lý 10 Kết Nối Tri Thức
Giải bài tập Lý 10 CTST
Giải bài tập Lý 10 Cánh Diều
Trắc nghiệm Vật Lý 10
Hoá học 10
Hóa học 10 Kết Nối Tri Thức
Hóa học 10 Chân Trời Sáng Tạo
Hóa học 10 Cánh Diều
Giải bài tập Hóa 10 Kết Nối Tri Thức
Giải bài tập Hóa 10 CTST
Giải bài tập Hóa 10 Cánh Diều
Trắc nghiệm Hóa 10
Sinh học 10
Sinh học 10 Kết Nối Tri Thức
Sinh học 10 Chân Trời Sáng Tạo
Sinh học 10 Cánh Diều
Giải bài tập Sinh 10 Kết Nối Tri Thức
Giải bài tập Sinh 10 CTST
Giải bài tập Sinh 10 Cánh Diều
Trắc nghiệm Sinh học 10
Lịch sử 10
Lịch Sử 10 Kết Nối Tri Thức
Lịch Sử 10 Chân Trời Sáng Tạo
Lịch Sử 10 Cánh Diều
Giải bài tập Lịch Sử 10 KNTT
Giải bài tập Lịch Sử 10 CTST
Giải bài tập Lịch Sử 10 Cánh Diều
Trắc nghiệm Lịch sử 10
Địa lý 10
Địa Lý 10 Kết Nối Tri Thức
Địa Lý 10 Chân Trời Sáng Tạo
Địa Lý 10 Cánh Diều
Giải bài tập Địa Lý 10 KNTT
Giải bài tập Địa Lý 10 CTST
Giải bài tập Địa Lý 10 Cánh Diều
Trắc nghiệm Địa lý 10
GDKT & PL 10
GDKT & PL 10 Kết Nối Tri Thức
GDKT & PL 10 Chân Trời Sáng Tạo
GDKT & PL 10 Cánh Diều
Giải bài tập GDKT & PL 10 KNTT
Giải bài tập GDKT & PL 10 CTST
Giải bài tập GDKT & PL 10 CD
Trắc nghiệm GDKT & PL 10
Công nghệ 10
Công nghệ 10 Kết Nối Tri Thức
Công nghệ 10 Chân Trời Sáng Tạo
Công nghệ 10 Cánh Diều
Giải bài tập Công nghệ 10 KNTT
Giải bài tập Công nghệ 10 CTST
Giải bài tập Công nghệ 10 CD
Trắc nghiệm Công nghệ 10
Tin học 10
Tin học 10 Kết Nối Tri Thức
Tin học 10 Chân Trời Sáng Tạo
Tin học 10 Cánh Diều
Giải bài tập Tin học 10 KNTT
Giải bài tập Tin học 10 CTST
Giải bài tập Tin học 10 Cánh Diều
Trắc nghiệm Tin học 10
Cộng đồng
Hỏi đáp lớp 10
Tư liệu lớp 10
Xem nhiều nhất tuần
Đề thi giữa HK1 lớp 10
Đề thi giữa HK2 lớp 10
Đề thi HK1 lớp 10
Đề thi HK2 lớp 10
Video bồi dưỡng HSG môn Toán
Toán 10 Chân trời sáng tạo Bài 2: Tập hợp
Toán 10 Kết nối tri thức Bài 1: Mệnh đề
Toán 10 Cánh Diều Bài tập cuối chương 1
Soạn bài Thần Trụ Trời - Ngữ văn 10 CTST
Soạn bài Ra-ma buộc tội - Ngữ văn 10 Tập 1 Cánh Diều
Soạn bài Chữ người tử tù - Nguyễn Tuân - Ngữ văn 10 KNTT
Văn mẫu về Chữ người tử tù
Văn mẫu về Tây Tiến
Văn mẫu về Cảm xúc mùa thu (Thu hứng)
Văn mẫu về Bình Ngô đại cáo
YOMEDIA YOMEDIA ×Thông báo
Bạn vui lòng đăng nhập trước khi sử dụng chức năng này.
Bỏ qua Đăng nhập ×Thông báo
Bạn vui lòng đăng nhập trước khi sử dụng chức năng này.
Đồng ý ATNETWORK ON QC Bỏ qua >>
QC Bỏ qua >> 
Từ khóa » Sơ đồ Tư Duy Toán Lớp 10
-
Tổng Hợp Bài Giảng Sơ đồ Tư Duy Các Môn Lớp 10
-
Toán Học 10 – Sơ đồ Tư Duy - Trung Tâm Gia Sư Dạy Kèm Tại Nhà ...
-
Sơ đồ Tư Duy Toán 10 - TopLoigiai
-
Sơ đồ Tư Duy Môn Toán Lớp 10 - 123doc
-
Củng Cố Kiến Thức Toán 10 Bằng Sơ đồ Tư Duy Và Hệ Thống Câu Hỏi ...
-
Top 9 Sơ đồ Tư Duy Toán 10 Chương 1 đại Số 2022
-
SƠ ĐỒ TƯ DUY MÔN TOÁN LỚP 10
-
Sơ đồ Tư Duy Môn Toán Lớp 10 - Trường Online
-
Sơ Đồ Tư Duy Toán 10 Chương 1 0 Đại Số, Sơ Đồ ...
-
Cách Vẽ Sơ Đồ Tư Duy Môn Toán, Hướng Dẫn Vẽ ...
-
Vẽ Sơ Đồ Tư Duy Toán 10 Chương 2 Hình Học 10Chương 2, Lập ...
-
Lập Sơ đồ Tư Duy Hình Học 10 Chương... | Xem Lời Giải Tại QANDA
.PNG)
.PNG)
.PNG)
.PNG)