Toán 10 Ôn Tập Chương 6 Cung Góc Lương Giác Và Công Thức ...

YOMEDIA NONE Trang chủ Toán 10 Chương 6: Cung Và Góc Lượng Giác. Công Thức Lượng Giác Toán 10 Ôn tập chương 6 Cung Góc lương giác và Công thức lượng giác ADMICRO Lý thuyết10 Trắc nghiệm47 BT SGK 575 FAQ

Bài học Ôn chương 6 sẽ giúp các em hệ thống lại toàn bộ kiến thức của Cung và góc lượng giác, Công thức lượng giác cũng như phương pháp giải các dạng bài tập liên quan đến lượng giác

ATNETWORK YOMEDIA

1. Tóm tắt lý thuyết

1.1 Quan hệ giữa độ và radian

1.2. Giá trị lượng giác của \(\alpha \)

1.3. Công thức lượng giác cơ bản

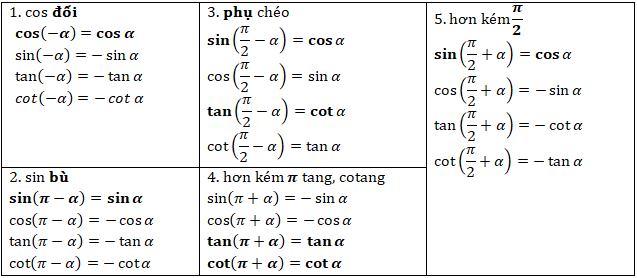
1.4. Công thức cung liên kết

1.5. Công thức cộng

1.6. Công thức nhân đôi - nhân ba - hạ bậc

1.7. Công thức biến đổi tổng thành tích - tích thành tổng

2. Bài tập minh hoạ

3. Luyện tập bài 4 chương 6 đại số 10

3.1. Trắc nghiệm về Cung và góc lượng giác, công thức lượng giác

3.2. Bài tập SGK & Nâng cao về Cung và góc lượng giác, công thức lượng giác

4. Hỏi đáp về bài 4 chương 6 đại số 10

Tóm tắt lý thuyết

Các kiến thức cần nhớ

1.1. Quan hệ giữa độ và rađian

\({180^ \circ } = \pi {\rm{ }}rad\)

Các góc đặc biệt \(0;\frac{\pi }{6};\frac{\pi }{4};\frac{\pi }{3};\frac{\pi }{2};\pi \)

1.2. Giá trị lượng giác của \(\alpha \)

\(\begin{array}{l} 1.\sin \left( {\alpha + k2\pi } \right) = \sin \alpha \;\;\;\left( {k \in Z} \right)\\ \cos \left( {\alpha + k2\pi } \right) = \cos \alpha \;\;\;\left( {k \in Z} \right)\\ \tan \left( {\alpha + k\pi } \right)\;\;\; = \tan \alpha \;\;\;\left( {k \in Z} \right)\\ \cot \left( {\alpha + k\pi } \right)\;\;\; = \cot \alpha \;\;\;\left( {k \in Z} \right) \end{array}\) \(2.\left| {\sin \alpha } \right| \le 1\;\;\;\;\;\left| {\cos \alpha } \right| \le 1\)

1.3. Công thức lượng giác cơ bản

1.4. Công thức cung liên kết

1.5. Công thức cộng

1.6. Công thức nhân đôi - nhân ba - hạ bậc

1.7. Công thức biến đổi tổng thành tích - tích thành tổng

Bài tập minh họa

Dạng 1: Chứng minh đẳng thức lượng giác

1. Phương pháp:

Muốn chứng minh 1 đẳng thức lượng giác, ta dùng công thức lượng giác để biến đổi biểu thức lượng giác ở 1 vế thành biểu thức lượng giác ở vế kia.

Để ý rằng 1 biểu thức lượng giác có thể biến đổi thành nhiều dạng khác nhau. Ví dụ:

\({\sin ^2}2x = 1 - {\cos ^2}2x\) (CT LG cơ bản)

\({\sin ^2}2x = \frac{1}{2}\left( {1 - \cos 4x} \right)\) (CT hạ bậc)

\({\sin ^2}2x = 4{\sin ^2}x.{\cos ^2}x\) (CT nhân đôi)

Tùy theo mỗi bài toán, ta chọn CT thích hợp để biến đổi

2. Ví dụ minh họa

Ví dụ 1: Chứng minh

\(a.\;{\sin ^4}\alpha + {\cos ^4}\alpha = 1 - \frac{1}{2}{\sin ^2}2\alpha \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;b.\;{\sin ^6}\alpha + {\cos ^6}\alpha = 1 - \frac{3}{4}{\sin ^2}2\alpha \)

Hướng dẫn: Áp dụng CT LG cơ bản và HĐT \({a^2} + {b^2} = {\left( {a + b} \right)^2} - 2ab{\rm{ }}{a^3} + {b^3} = {\left( {a + b} \right)^3} - 3ab\left( {a + b} \right)\)

\(a.\;{\sin ^4}\alpha + {\cos ^4}\alpha = {\left( {{\rm{si}}{{\rm{n}}^2}\alpha } \right)^2} + {\left( {{\rm{co}}{{\rm{s}}^2}\alpha } \right)^2} = {\left( {{\rm{si}}{{\rm{n}}^2}\alpha + {\rm{co}}{{\rm{s}}^2}\alpha } \right)^2} - 2{\rm{si}}{{\rm{n}}^2}\alpha .{\rm{co}}{{\rm{s}}^2}\alpha \)

\( = 1 - \frac{1}{2}{\left( {2\sin \alpha .\cos \alpha } \right)^2} = 1 - \frac{1}{2}{\sin ^2}2\alpha \)

\(b.\;{\sin ^6}\alpha + {\cos ^6}\alpha = {\left( {{\rm{si}}{{\rm{n}}^2}\alpha } \right)^3} + {\left( {{\rm{co}}{{\rm{s}}^2}\alpha } \right)^3} = {\left( {{\rm{si}}{{\rm{n}}^2}\alpha + {\rm{co}}{{\rm{s}}^2}\alpha } \right)^3} - 3{\rm{si}}{{\rm{n}}^2}\alpha .{\rm{co}}{{\rm{s}}^2}\alpha \left( {{\rm{si}}{{\rm{n}}^2}\alpha + {\rm{co}}{{\rm{s}}^2}\alpha } \right)\)

\( = 1 - 3si{n^2}\alpha .co{s^2}\alpha = 1 - \frac{3}{4}{\sin ^2}2\alpha \)

Ví dụ 2: Chứng minh

\(a.\cos 3a.{\rm{si}}{{\rm{n}}^3}a + \sin 3a.{\rm{co}}{{\rm{s}}^3}a = \frac{3}{4}\sin 4a\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;b.\;\cos 3a.{\rm{co}}{{\rm{s}}^3}a + \sin 3a.{\rm{si}}{{\rm{n}}^3}a = {\rm{co}}{{\rm{s}}^3}2a\)

Hướng dẫn: Áp dụng CT nhân ba – CT cộng \(4{\rm{si}}{{\rm{n}}^3}a = 3\sin a - \sin 3a\;\;\;\;\;\;\;4{\rm{co}}{{\rm{s}}^3}a = \cos 3a + 3\cos a\)

\(\begin{array}{l} a.\cos 3a.{\rm{si}}{{\rm{n}}^3}a + \sin 3a.{\rm{co}}{{\rm{s}}^3}a = \cos 3a\frac{{3\sin a - \sin 3a}}{4} + \sin 3a\frac{{\cos 3a + 3\cos a}}{4}\\ = \frac{1}{4}\left[ {\cos 3a\left( {3\sin a - \sin 3a} \right) + \sin 3a\left( {\cos 3a + 3\cos a} \right)} \right]\\ = \frac{1}{4}\left( {3\sin a.\cos 3a - \cos 3a.\sin 3a + \sin 3a.\cos 3a + 3.\cos a.\sin 3a} \right)\\ = \frac{3}{4}\left( {\sin a.\cos 3a + \cos a.\sin 3a} \right) = \frac{3}{4}\sin \left( {a + 3a} \right) = \frac{3}{4}\sin 4a \end{array}\)

\(\begin{array}{l} b.\cos 3a.{\rm{co}}{{\rm{s}}^3}a + \sin 3a.{\rm{si}}{{\rm{n}}^3}a = \frac{1}{4}\left[ {\cos 3a\left( {\cos 3a + 3\cos a} \right) + \sin 3a\left( {3\sin a - \sin 3a} \right)} \right]\\ = \frac{1}{4}\left( {{\rm{co}}{{\rm{s}}^3}3a + 3\cos 3a.\cos a + 3.\sin a.\sin 3a - {\rm{si}}{{\rm{n}}^3}3a} \right)\\ = \frac{1}{4}\left[ {{\rm{co}}{{\rm{s}}^3}3a - {\rm{si}}{{\rm{n}}^3}3a + 3\left( {\cos 3a.\cos a + \sin a.\sin 3a} \right)} \right]\\ = \frac{1}{4}\left[ {\cos 6a + 3\cos \left( {3a - a} \right)} \right]\\ = \frac{1}{4}\left( {4{\rm{co}}{{\rm{s}}^3}2a - 3\cos 2a + 3\cos 2a} \right) = {\rm{co}}{{\rm{s}}^3}2a \end{array}\)

Ví dụ 3: Chứng minh

\(\begin{array}{l} a.\sin \left( {a + b} \right).\sin \left( {a - b} \right) = {\rm{co}}{{\rm{s}}^2}a - {\rm{co}}{{\rm{s}}^2}b\;\\ b.\sin x.\sin \left( {\frac{\pi }{3} - x} \right).\sin \left( {\frac{\pi }{3} + x} \right) = \frac{1}{4}\sin 3x\\ c.\tan x.\tan \left( {\frac{\pi }{3} - x} \right).\tan \left( {\frac{\pi }{3} + x} \right) = \tan 3x\;\;\;\;\;\;\;\;\;\;\;\;\; \end{array}\)

Hướng dẫn: Áp dụng CT biến đổi tích thành tổng

\(a.\sin \left( {a + b} \right).\sin \left( {a - b} \right) = \frac{1}{2}\left( {\cos 2b - \cos 2a} \right) = \frac{1}{2}\left[ {2{{\cos }^2}b - 1 - \left( {2{{\cos }^2}a - 1} \right)} \right] = {\rm{co}}{{\rm{s}}^2}b - {\rm{co}}{{\rm{s}}^2}a\)

\(\begin{array}{l} b.\sin x.\sin \left( {\frac{\pi }{3} - x} \right).\sin \left( {\frac{\pi }{3} + x} \right) = \frac{1}{2}\sin x\left( {\cos 2x - \cos \frac{{2\pi }}{3}} \right) = \frac{1}{2}\sin x.\cos 2x - \frac{1}{4}\sin x\\ = \frac{1}{4}\left( {\sin 3x - \sin x} \right) - \frac{1}{4}\sin x = \frac{1}{4}\sin 3x \end{array}\)

\(\begin{array}{l} c.\tan x.\tan \left( {\frac{\pi }{3} - x} \right).\tan \left( {\frac{\pi }{3} + x} \right) = \tan x.\frac{{\tan \frac{\pi }{3} - \tan x}}{{1 + \tan \frac{\pi }{3}.\tan x}}.\frac{{\tan \frac{\pi }{3} + \tan x}}{{1 - \tan \frac{\pi }{3}.\tan x}}\\ = \tan x.\frac{{\sqrt 3 - \tan x}}{{1 + \sqrt 3 \tan x}}.\frac{{\sqrt 3 + \tan x}}{{1 - \sqrt 3 \tan x}}\\ = \tan x.\frac{{3 - {{\tan }^2}x}}{{1 - 3{{\tan }^2}x}} = \tan 3x \end{array}\)

Dạng 2: Rút gọn, tính giá trị của 1 biểu thức lượng giác

1. Phương pháp

Muốn rút gọn 1 biểu thức lượng giác, ta dung các CTLG để biến đổi biểu thức đã cho.

Muốn tính giá trị của 1 biểu thức lượng giác, ta tìm cách rút gọn biểu thức này. Ngoài việc dùng các CTLG, nên xem xét biểu thức đã cho có dạng gì đặc biệt, từ đó chọn cách giải thích hợp.

2. Ví dụ minh họa

Ví dụ 1: Rút gọn các biểu thức sau

\(\begin{array}{l} a.A = \;\sin \left( {2x + \frac{\pi }{3}} \right).\cos \left( {x - \frac{\pi }{6}} \right) - \cos \left( {\frac{{2\pi }}{3} - x} \right).\cos \left( {2x + \frac{\pi }{3}} \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\\ b.\;B = \cos x + \cos \left( {x + \frac{{2\pi }}{3}} \right) + \cos \left( {x - \frac{{2\pi }}{3}} \right) \end{array}\)

Hướng dẫn: Áp dụng CT cung phụ - CT biến đổi tổng thành tích – tích thành tổng

a. Ta có \(\;\frac{{2\pi }}{3} - x = \frac{\pi }{2} - \left( {x - \frac{\pi }{6}} \right) \Rightarrow \cos \left( {\frac{{2\pi }}{3} - x} \right) = \cos \left[ {\frac{\pi }{2} - \left( {x - \frac{\pi }{6}} \right)} \right] = \sin \left( {x - \frac{\pi }{6}} \right)\)

\(\begin{array}{l} A = \;\sin \left( {2x + \frac{\pi }{3}} \right).\cos \left( {x - \frac{\pi }{6}} \right) - \cos \left( {\frac{{2\pi }}{3} - x} \right).\cos \left( {2x + \frac{\pi }{3}} \right)\\ = \sin \left( {2x + \frac{\pi }{3}} \right).\cos \left( {x - \frac{\pi }{6}} \right) - \sin \left( {x - \frac{\pi }{6}} \right).\cos \left( {2x + \frac{\pi }{3}} \right)\\ = \sin \left[ {\left( {2x + \frac{\pi }{3}} \right) - \left( {x - \frac{\pi }{6}} \right)} \right] = \sin \left( {x + \frac{\pi }{2}} \right) = \cos x \end{array}\)

\(\begin{array}{l} b. B = \cos x + \cos \left( {x + \frac{{2\pi }}{3}} \right) + \cos \left( {x - \frac{{2\pi }}{3}} \right)\\ = \cos x + \left[ {\cos \left( {x + \frac{{2\pi }}{3}} \right) + \cos \left( {x - \frac{{2\pi }}{3}} \right)} \right]\\ = \cos x + 2\cos x.\cos \frac{{2\pi }}{3} = \cos x + 2\cos x.\left( { - \frac{1}{2}} \right)\\ = \cos x - \cos x = 0 \end{array}\)

Ví dụ 2: Chứng minh các biểu thức sau không phụ vào:

\(\begin{array}{l} a.\;A = 3\left( {{{\sin }^4}x + {{\cos }^4}x} \right) - 2\left( {{{\sin }^6}x + {{\cos }^6}x} \right)\\ b.\;B = {\cos ^2}x + {\cos ^2}\left( {x + a} \right) - 2\cos a.\cos x.\cos \left( {x + a} \right)\\ c.\;C = {\cos ^2}x + {\sin ^2}\left( {x + a} \right) - 2\sin a.\cos x.\sin \left( {x + a} \right) \end{array}\)

Hướng dẫn: Áp dụng CT biến đổi tổng thành tích – tích thành tổng và HĐT

\(\begin{array}{l} a.\;A = 3\left( {{{\sin }^4}x + {{\cos }^4}x} \right) - 2\left( {{{\sin }^6}x + {{\cos }^6}x} \right)\\ = 3{\sin ^4}x + 3{\cos ^4}x - 2\left( {{{\sin }^2}x + {{\cos }^2}x} \right)\left( {{{\sin }^4}x - {{\sin }^2}x.{{\cos }^2}x + {{\cos }^4}x} \right)\\ = 3{\sin ^4}x + 3{\cos ^4}x - 2{\sin ^4}x + 2{\sin ^2}x.{\cos ^2}x - 2{\cos ^4}x\\ = {\sin ^4}x + 2{\sin ^2}x.{\cos ^2}x + {\cos ^4}x\\ = {\left( {{{\sin }^2}x + {{\cos }^2}x} \right)^2} = 1,\;\forall x \end{array}\)

Vậy A không phụ thuộc vào x

\(\begin{array}{l} b.\;B = {\cos ^2}x + {\cos ^2}\left( {x + a} \right) - \cos a.\left[ {2\cos x.\cos \left( {x + a} \right)} \right]\\ = \frac{1}{2}\left( {1 + \cos 2x} \right) + \frac{1}{2}\left[ {1 + \cos \left( {2x + 2a} \right)} \right] - \cos a\left[ {\cos \left( {2x + a} \right) + \cos a} \right]\\ = 1 + \frac{1}{2}\left[ {\cos 2x + \cos \left( {2x + 2a} \right)} \right] - \cos a.\cos \left( {2x + a} \right) - {\cos ^2}a\\ = 1 + \cos a.\cos \left( {2x + a} \right) - \cos a.\cos \left( {2x + a} \right) - {\cos ^2}a\\ = 1 - {\cos ^2}a = {\sin ^2}a,\;\forall x \end{array}\)

Vậy B không phụ thuộc vào x

\(\begin{array}{l} c.\;C = {\cos ^2}x + {\sin ^2}\left( {x + a} \right) - 2\sin a.\cos x.\sin \left( {x + a} \right)\\ = 1 + \frac{1}{2}\left[ {\cos 2x - \cos \left( {2x + 2a} \right)} \right] - \sin a\left[ {\sin \left( {2x + a} \right) + \sin a} \right]\\ = 1 - \sin \left( {2x + a} \right).\sin \left( { - a} \right) - \sin \left( {2x + a} \right).\sin a - {\sin ^2}a\\ = 1 - {\sin ^2}a = {\cos ^2}a,\;\forall x \end{array}\)

Vậy C không phụ thuộc vào x

Ví dụ 3: Tính giá trị biểu thức

\(\begin{array}{l} a.A = \frac{1}{{\sin 10^\circ }} - 4\sin 70^\circ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\\ b.\;B = \sin 20^\circ .\sin 40^\circ .\sin 80^\circ \\ c.C = \cos \frac{\pi }{9} + \cos \frac{{5\pi }}{9} + \cos \frac{{7\pi }}{9}\; \end{array}\)

Hướng dẫn: Áp dụng CT phụ - CT tổng thành tích–tích thành tổng

\(\begin{array}{l} a.A = \frac{1}{{\sin 10^\circ }} - 4\sin 70^\circ = \frac{1}{{\sin 10^\circ }} - 4\cos 20^\circ = \frac{{1 - 4\cos 20^\circ .\sin 10^\circ }}{{\sin 10^\circ }}\\ = \frac{{1 - 2\left( {\cos 30^\circ - \sin 10^\circ } \right)}}{{\sin 10^\circ }} = \frac{{2\sin 10^\circ }}{{\sin 10^\circ }} = 2 \end{array}\)

\(\begin{array}{*{20}{l}} \begin{array}{l} b.\;B = \sin {20^^\circ }.\sin {40^^\circ }.\sin {80^^\circ }\\ = \frac{1}{2}\sin {20^^\circ }\left( {\cos {{40}^^\circ } - \cos {{120}^^\circ }} \right)\\ = \frac{1}{2}\sin {20^^\circ }.\cos {40^^\circ } + \frac{1}{4}\sin {20^^\circ } \end{array}\\ \begin{array}{l} = \frac{1}{4}\left( {\sin {{60}^^\circ } - \sin {{20}^^\circ }} \right) + \frac{1}{4}\sin {20^^\circ }\\ = \frac{1}{4}\sin {60^^\circ } = \frac{{\sqrt 3 }}{8} \end{array} \end{array}\)

\(c.C = \cos \frac{\pi }{9} + \left( {\cos \frac{{5\pi }}{9} + \cos \frac{{7\pi }}{9}} \right) = \cos \frac{\pi }{9} + 2\cos \frac{{6\pi }}{9}.\cos \frac{\pi }{9} = \cos \frac{\pi }{9} - \cos \frac{\pi }{9} = 0\)

3. Luyện tập Bài 4 chương 6 đại số 10

Bài học Ôn chương 6 sẽ giúp các em hệ thống lại toàn bộ kiến thức của Cung và góc lượng giác, Công thức lượng giác cũng như phương pháp giải các dạng bài tập liên quan đến lượng giác

3.1 Trắc nghiệm về cung và góc lượng giác, công thức lượng giác

Để cũng cố bài học xin mời các em cũng làm Bài kiểm tra Trắc nghiệm Ôn tập chương VI - Toán 10 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.

• Câu 1:

  Tính giá trị các hàm số lượng giác của góc \(\alpha = \;{240^0}\)

  • A. \(\cos \alpha = \;\frac{1}{2}\;;\;\;\sin \alpha = \;\frac{{\sqrt 3 }}{2}\;;\quad \tan \alpha \; = \;\sqrt 3 \;;\;\;\cot \alpha = \;\frac{1}{{\sqrt 3 }}\)
  • B. \(\cos \alpha = \; - \frac{1}{2}\;;\;\;\sin \alpha = \; - \frac{{\sqrt 3 }}{2}\;;\quad \tan \alpha \; = \; - \sqrt 3 \;;\;\;\cot \alpha = \; - \frac{1}{{\sqrt 3 }}\)
  • C. \(\cos \alpha = \; - \frac{{\sqrt 2 }}{2}\;;\;\;\sin \alpha = \;\frac{{\sqrt 2 }}{2}\;;\quad \tan \alpha \; = \; - 1\;;\;\;\cot \alpha = \; - 1\)
  • D. \(\cos \alpha = \;\frac{{\sqrt 3 }}{2}\;;\;\;\sin \alpha = \; - \frac{1}{2}\;;\quad \tan \alpha \; = \; - \frac{1}{{\sqrt 3 }}\;;\;\;\cot \alpha = \; - \sqrt 3 \)

• Câu 2:

  Đơn giản biểu thức \(D = \tan x + \frac{{\cos x}}{{1 + \sin x}}\)

  • A. \(\frac{1}{{\sin x}}\)
  • B. \(\frac{1}{{\cos x}}\)
  • C. cosx
  • D. sinx

• Câu 3:

  Đơn giản biểu thức \(E = \cot x + \frac{{\sin x}}{{1 + \cos x}}\)

  • A. \(\frac{1}{{\sin x}}\)
  • B. \(\frac{1}{{\cos x}}\)
  • C. cosx
  • D. sinx

Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!

3.2 Bài tập SGK và Nâng Cao về cung và góc lượng giác, công thức lượng giác

Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Ôn tập chương VI - Toán 10 sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK Đại số 10 Cơ bản và Nâng cao.

Bài tập 1 trang 155 SGK Đại số 10

Bài tập 2 trang 155 SGK Đại số 10

Bài tập 3 trang 155 SGK Đại số 10

Bài tập 4 trang 155 SGK Đại số 10

Bài tập 5 trang 156 SGK Đại số 10

Bài tập 6 trang 156 SGK Đại số 10

Bài tập 7 trang 156 SGK Đại số 10

Bài tập 8 trang 156 SGK Đại số 10

Bài tập 9 trang 157 SGK Đại số 10

Bài 10 trang 157 SGK Đại số 10

Bài tập 11 trang 157 SGK Đại số 10

Bài tập 12 trang 157 SGK Đại số 10

Bài tập 13 trang 157 SGK Đại số 10

Bài tập 14 trang 157 SGK Đại số 10

Bài tập 6.42 trang 191 SBT Toán 10

Bài tập 6.43 trang 191 SBT Toán 10

Bài tập 6.44 trang 191 SBT Toán 10

Bài tập 6.45 trang 191 SBT Toán 10

Bài tập 6.46 trang 192 SBT Toán 10

Bài tập 6.47 trang 192 SBT Toán 10

Bài tập 6.48 trang 192 SBT Toán 10

Bài tập 6.49 trang 192 SBT Toán 10

Bài tập 6.50 trang 192 SBT Toán 10

Bài tập 6.51 trang 192 SBT Toán 10

Bài tập 6.52 trang 192 SBT Toán 10

Bài tập 6.53 trang 192 SBT Toán 10

Bài tập 6.54 trang 193 SBT Toán 10

Bài tập 6.55 trang 193 SBT Toán 10

Bài tập 6.56 trang 193 SBT Toán 10

Bài tập 6.57 trang 193 SBT Toán 10

Bài tập 6.59 trang 193 SBT Toán 10

Bài tập 6.58 trang 193 SBT Toán 10

Bài tập 55 trang 217 SGK Toán 10 NC

Bài tập 56 trang 218 SGK Toán 10 NC

Bài tập 57 trang 218 SGK Toán 10 NC

Bài tập 58 trang 218 SGK Toán 10 NC

Bài tập 59 trang 218 SGK Toán 10 NC

Bài tập 60 trang 219 SGK Toán 10 NC

Bài tập 61 trang 219 SGK Toán 10 NC

Bài tập 62 trang 219 SGK Toán 10 NC

Bài tập 63 trang 219 SGK Toán 10 NC

Bài tập 64 trang 219 SGK Toán 10 NC

Bài tập 65 trang 219 SGK Toán 10 NC

Bài tập 66 trang 219 SGK Toán 10 NC

Bài tập 67 trang 220 SGK Toán 10 NC

Bài tập 68 trang 220 SGK Toán 10 NC

Bài tập 69 trang 220 SGK Toán 10 NC

4. Hỏi đáp về bài 4 chương 6 đại số 10

Nếu có thắc mắc cần giải đáp các em có thể để lại câu hỏi trong phần Hỏi đáp, cộng đồng Toán HỌC247 sẽ sớm trả lời cho các em.

-- Mod Toán Học 10 HỌC247

NONE

Bài học cùng chương

Toán 10 Bài 1: Cung và góc lượng giác Toán 10 Bài 2: Giá trị lượng giác của một cung Toán 10 Bài 3: Công thức lượng giác ADSENSE TRACNGHIEM Bộ đề thi nổi bật UREKA AANETWORK

XEM NHANH CHƯƠNG TRÌNH LỚP 10

Toán 10

Toán 10 Kết Nối Tri Thức

Toán 10 Chân Trời Sáng Tạo

Toán 10 Cánh Diều

Giải bài tập Toán 10 Kết Nối Tri Thức

Giải bài tập Toán 10 CTST

Giải bài tập Toán 10 Cánh Diều

Trắc nghiệm Toán 10

Ngữ văn 10

Ngữ Văn 10 Kết Nối Tri Thức

Ngữ Văn 10 Chân Trời Sáng Tạo

Ngữ Văn 10 Cánh Diều

Soạn Văn 10 Kết Nối Tri Thức

Soạn Văn 10 Chân Trời Sáng tạo

Soạn Văn 10 Cánh Diều

Văn mẫu 10

Tiếng Anh 10

Giải Tiếng Anh 10 Kết Nối Tri Thức

Giải Tiếng Anh 10 CTST

Giải Tiếng Anh 10 Cánh Diều

Trắc nghiệm Tiếng Anh 10 KNTT

Trắc nghiệm Tiếng Anh 10 CTST

Trắc nghiệm Tiếng Anh 10 CD

Giải Sách bài tập Tiếng Anh 10

Vật lý 10

Vật lý 10 Kết Nối Tri Thức

Vật lý 10 Chân Trời Sáng Tạo

Vật lý 10 Cánh Diều

Giải bài tập Lý 10 Kết Nối Tri Thức

Giải bài tập Lý 10 CTST

Giải bài tập Lý 10 Cánh Diều

Trắc nghiệm Vật Lý 10

Hoá học 10

Hóa học 10 Kết Nối Tri Thức

Hóa học 10 Chân Trời Sáng Tạo

Hóa học 10 Cánh Diều

Giải bài tập Hóa 10 Kết Nối Tri Thức

Giải bài tập Hóa 10 CTST

Giải bài tập Hóa 10 Cánh Diều

Trắc nghiệm Hóa 10

Sinh học 10

Sinh học 10 Kết Nối Tri Thức

Sinh học 10 Chân Trời Sáng Tạo

Sinh học 10 Cánh Diều

Giải bài tập Sinh 10 Kết Nối Tri Thức

Giải bài tập Sinh 10 CTST

Giải bài tập Sinh 10 Cánh Diều

Trắc nghiệm Sinh học 10

Lịch sử 10

Lịch Sử 10 Kết Nối Tri Thức

Lịch Sử 10 Chân Trời Sáng Tạo

Lịch Sử 10 Cánh Diều

Giải bài tập Lịch Sử 10 KNTT

Giải bài tập Lịch Sử 10 CTST

Giải bài tập Lịch Sử 10 Cánh Diều

Trắc nghiệm Lịch sử 10

Địa lý 10

Địa Lý 10 Kết Nối Tri Thức

Địa Lý 10 Chân Trời Sáng Tạo

Địa Lý 10 Cánh Diều

Giải bài tập Địa Lý 10 KNTT

Giải bài tập Địa Lý 10 CTST

Giải bài tập Địa Lý 10 Cánh Diều

Trắc nghiệm Địa lý 10

GDKT & PL 10

GDKT & PL 10 Kết Nối Tri Thức

GDKT & PL 10 Chân Trời Sáng Tạo

GDKT & PL 10 Cánh Diều

Giải bài tập GDKT & PL 10 KNTT

Giải bài tập GDKT & PL 10 CTST

Giải bài tập GDKT & PL 10 CD

Trắc nghiệm GDKT & PL 10

Công nghệ 10

Công nghệ 10 Kết Nối Tri Thức

Công nghệ 10 Chân Trời Sáng Tạo

Công nghệ 10 Cánh Diều

Giải bài tập Công nghệ 10 KNTT

Giải bài tập Công nghệ 10 CTST

Giải bài tập Công nghệ 10 CD

Trắc nghiệm Công nghệ 10

Tin học 10

Tin học 10 Kết Nối Tri Thức

Tin học 10 Chân Trời Sáng Tạo

Tin học 10 Cánh Diều

Giải bài tập Tin học 10 KNTT

Giải bài tập Tin học 10 CTST

Giải bài tập Tin học 10 Cánh Diều

Trắc nghiệm Tin học 10

Cộng đồng

Hỏi đáp lớp 10

Tư liệu lớp 10

Xem nhiều nhất tuần

Đề thi giữa HK1 lớp 10

Đề thi giữa HK2 lớp 10

Đề thi HK1 lớp 10

Đề thi HK2 lớp 10

Video bồi dưỡng HSG môn Toán

Toán 10 Chân trời sáng tạo Bài 2: Tập hợp

Toán 10 Kết nối tri thức Bài 1: Mệnh đề

Toán 10 Cánh Diều Bài tập cuối chương 1

Soạn bài Thần Trụ Trời - Ngữ văn 10 CTST

Soạn bài Ra-ma buộc tội - Ngữ văn 10 Tập 1 Cánh Diều

Soạn bài Chữ người tử tù - Nguyễn Tuân - Ngữ văn 10 KNTT

Văn mẫu về Bình Ngô đại cáo

Văn mẫu về Chữ người tử tù

Văn mẫu về Tây Tiến

Văn mẫu về Cảm xúc mùa thu (Thu hứng)

YOMEDIA YOMEDIA ×

Thông báo

Bạn vui lòng đăng nhập trước khi sử dụng chức năng này.

Bỏ qua Đăng nhập ×

Thông báo

Bạn vui lòng đăng nhập trước khi sử dụng chức năng này.

Đồng ý ATNETWORK ON QC Bỏ qua >>