Toán 11 Bài 5: Phép Quay

Trang chủ » Phép Quay Toán 11 Lý Thuyết » Toán 11 Bài 5: Phép Quay

Có thể bạn quan tâm

Toán 11 Bài 5: Phép quay Lí thuyết và Bài tập Phép quay Toán 11 Bài trước Bài sau Lớp: Lớp 11 Môn: Toán Phân loại: Tài liệu Tính phí

Nâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi.

Tìm hiểu thêm » Mua ngay Từ 79.000đ Hỗ trợ Zalo

Phép quay Toán 11

  • A. Lí thuyết Phép quay
    • 1. Phép quay là gì?
    • 2. Tính chất của phép quay
    • 3. Biểu diễn ảnh của phép quay
    • 4. Bài tập ví dụ minh họa về phép quay
  • B. Giải Toán hình lớp 11 SGK Kết nối tri thức
  • C. Giải bài tập Toán hình lớp 11 SBT Kết nối tri thức

Lí thuyết và Bài tập Phép quay được VnDoc biên soạn bao gồm hướng dẫn lý thuyết và hướng dẫn giải cho từng bài tập sách giáo khoa và sách bài tập giúp các bạn học sinh luyện tập và hiểu rõ hơn về phần Phép dời hình và phép đồng dạng trong mặt phẳng. Qua đó giúp các bạn học sinh ôn tập, củng cố và rèn luyện thêm kiến thức đã học trong chương trình Toán 11, Mời các bạn học sinh và quý thầy cô cùng tham khảo chi tiết.

  • Tóm tắt toàn bộ lý thuyết và công thức Đại số 11
  • Tóm tắt toàn bộ lý thuyết và công thức Hình học 11
  • Bài tập Toán lớp 11: Đạo hàm
  • Bảng công thức lượng giác dùng cho lớp 10 - 11 - 12

Toán 11 Bài 5: Phép quay

Bản quyền thuộc về VnDoc.Nghiêm cấm mọi hình thức sao chép nhằm mục đích thương mại.

A. Lí thuyết Phép quay

1. Phép quay là gì?

  • Định nghĩa: Cho điểm O và góc lượng giác \alpha, phép biến hình biến O thành chính nó, biến mỗi điểm A thành điểm A' sao cho OA = OA' và góc lượng giác (OA, OA') = \alpha được gọi là phép quay tâm O góc \alpha.

Trong đó: O là tâm quay, \alpha là góc quay. Phép quay được kí hiệu là: Q_{(O,\alpha )}

  • Nếu a=(2k+1)\pi,k\in\mathbb{Z} là phép đối xứng tâm.
  • Nếu a=2k\pi,k\in\mathbb{Z} là phép đồng nhất.

2. Tính chất của phép quay

  • Phép quay là phép biến hình nên nó có đầy đủ tính chất của phép dời hình.
  • Phép quay biến đoạn thẳng thành đoạn thẳng bằng nó.
  • Biến tam giác thành tam giác bằng nó.
  • Biến đường tròn thành đường tròn có cùng bán kính.

Ta có: Q_{(O,\alpha)}(d)=d' khi đó:

  • 0<\alpha<\frac{\pi}{2}: góc giữa đường thẳng d và đường thẳng d' là \alpha
  • \frac{\pi}{2} <\alpha<\pigóc giữa hai đường thẳng d và d' bằng \pi-\alpha

3. Biểu diễn ảnh của phép quay

Cho tam giác ABC và điểm O. Hãy biểu diễn ảnh A'B'C' của tam giác ABC qua phép quay tâm O góc quay \frac{\pi}{2}

4. Bài tập ví dụ minh họa về phép quay

Câu 1: Cho tam giác ABC đều có O là trọng tâm, gọi D,E,F lần lượt là trung điểm các cạnh BC,CA,AB.

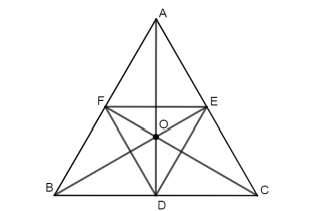
Phép quay thuận chiều tâm O góc quay 120° biến điểm F thành điểm nào dưới đây?

A. Điểm E. B. Điểm A. C. Điểm B. D. Điểm D

Hướng dẫn giải

Phép quay thuận chiều tâm O góc quay 120° biến điểm F thành điểm E.

Câu 2: Cho hình vuông ABCD tâm O.

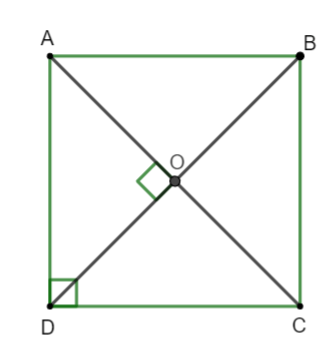
Khẳng định nào sau đây là đúng?

A. Phép quay ngược chiều tâm A góc quay 900 biến điểm B thành điểm D.

B. Phép quay ngược chiều tâm C góc quay 900 biến điểm B thành điểm D.

C. Phép quay thuận chiều tâm A góc quay 450 biến điểm B thành điểm C.

D. Phép quay ngược chiều tâm C góc quay 450 biến điểm B thành điểm A.

Hướng dẫn giải

Phép quay ngược chiều tâm C góc quay 900 biến điểm B thành điểm D.

Câu 3: Cho hình ngũ giác đều ABCDE tâm O.

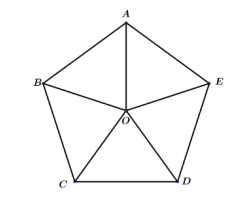
Phép quay ngược chiều tâm O góc quay 1440 biến điểm A thành điểm nào dưới đây?

A. Điểm B B. Điểm D C. Điểm E D. Điểm C

Hướng dẫn giải

Ta có ABCDE là ngũ giác đều nên

\widehat{AOB} = \widehat{BOC} = \widehat{COD} = \widehat{DOE} = \widehat{EOA} = \frac{360^{0}}{5} = 72^{0}

Mà góc quay 144^{0} = 2.72^{0}

=> Phép quay ngược chiều tâm O góc quay 1440 biến điểm A thành điểm C.

Câu 4: Cho tam giác đều ABC có tâm O và các đường cao AA';BB';CC', (các đỉnh của tam giác ghi theo chiều kim đồng hồ). Qua phép quay ngược chiều tâm O góc quay 2400 biến A và A′ thành:

A. A và A′ B. B và B′

C. C và C′ D. B và C

Hướng dẫn giải

Hình vẽ minh họa:

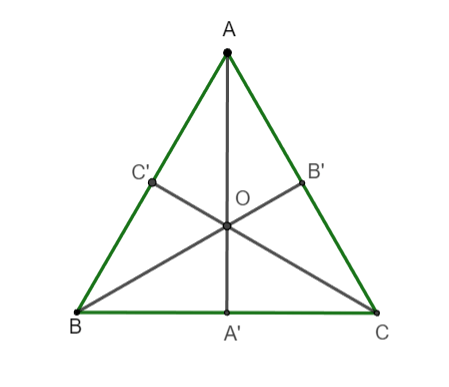
Qua phép quay ngược chiều tâm O góc quay 2400 biến điểm A và điểm A’ thành điểm B và B’.

Câu 5: Cho hình thoi ABCD có góc \widehat{ABC} = 60^{0} (các đỉnh của hình thoi ghi theo chiều kim đồng hồ). Qua phép quay ngược chiều tâm A góc quay 600 biến C và D thành:

A. A và B B. B và C

C. C và D D. D và A

Hướng dẫn giải

Hình vẽ minh họa:

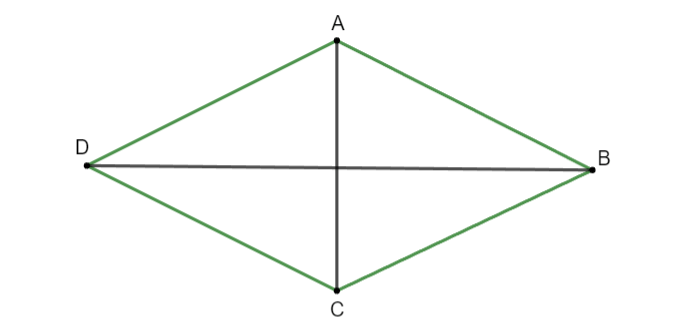
Qua phép quay ngược chiều tâm A góc quay 600 biến C và D thành B và C.

Câu 6: Cho hình lục giác ABCDEF, tâm O.

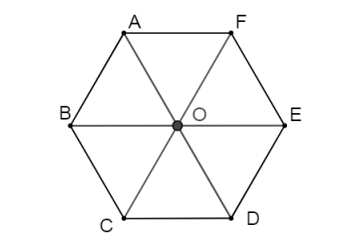
Khẳng định nào sau đây là sai?

A. Phép quay ngược chiều tâm O góc quay 600 biến tam giác BCD thành tam giác CDE.

B. Phép quay ngược chiều tâm O góc quay 1200 biến tam giác OEC thành tam giác OEA.

C. Phép quay thuận chiều tâm O góc quay 600 biến tam giác AFD thành tam giác FEC.

D. Phép quay thuận chiều tâm O góc quay 1200 biến tam giác BCD thành tam giác AFC.

Hướng dẫn giải

Phép quay ngược chiều tâm O góc quay 600 biến điểm B thành điểm C.

Phép quay ngược chiều tâm O góc quay 600 biến điểm C thành điểm D.

Phép quay ngược chiều tâm O góc quay 600 biến điểm D thành E.

=> Phép quay ngược chiều tâm O góc quay 600 biến tam giác BCD thành tam giác CDE.

B. Giải Toán hình lớp 11 SGK Kết nối tri thức

Trong Sách giáo khoa Toán lớp 11, các bạn học sinh chắc hẳn sẽ gặp những bài toán khó, phải tìm cách giải quyết. Hiểu được điều này, VnDoc đã tổng hợp và gửi tới các bạn học sinh lời giải và đáp án chi tiết cho các bài tập trong Sách giáo khoa Toán lớp 11. Mời các bạn học sinh tham khảo:

  • Giải bài tập Toán 11 Kết nối tri thức

C. Giải bài tập Toán hình lớp 11 SBT Kết nối tri thức

Sách bài tập Toán 11 tổng hợp các bài Toán từ cơ bản tới nâng cao, đi kèm với đó là đáp án. Tuy nhiên, nhiều đáp án không được giải chi tiết khiến cho các bạn học sinh gặp nhiều khó khăn khi tiếp xúc với dạng bài mới. VnDoc đã tổng hợp và gửi tới các bạn học sinh lời giải và đáp án chi tiết cho từng dạng bài tập trong Sách bài tập để các bạn có thể nắm vững, hiểu rõ hơn về dạng bài tập này. Mời các bạn học sinh tham khảo:

  • Giải SBT Toán 11 Sách Kết nối tri thức

------------------------------------

Trên đây VnDoc.com đã giới thiệu tới bạn đọc tài liệu: Toán 11 bài 5: Phép quay. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Hóa học lớp 10, Giải bài tập Hóa học lớp 11, Hóa học lớp 12, Thi THPT Quốc gia môn Văn, Thi THPT Quốc gia môn Lịch sử, Thi THPT Quốc gia môn Địa lý, Thi THPT Quốc gia môn Toán, đề thi học kì 1 lớp 11, đề thi học kì 2 lớp 11 mà VnDoc tổng hợp và đăng tải.

Từ khóa » Phép Quay Toán 11 Lý Thuyết