Toán 11 - Giới Hạn Của Hàm Số, Cách Tính Và Bài Tập áp Dụng
Có thể bạn quan tâm
Bài viết này sẽ tổng hợp một cách hệ thống và chi tiết về lý thuyết, các phương pháp giải và các dạng bài tập điển hình về giới hạn của hàm số.
A. Lý thuyết và các dạng Bài tập có lời giải chi tiết
I. Giới hạn hữu hạn
1. Giới hạn đặc biệt
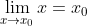
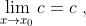 (c: hằng số)
(c: hằng số)
2. Định lý
a) Nếu: 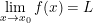 và
và 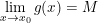 thì:
thì:
![small lim_{x ightarrow x_{0}}[f(x)+g(x)]=L+M](https://hayhochoi.vn/uploads/news/wyswyg/2020_07/15941830189y0r6m8g7d.gif)
![small lim_{x ightarrow x_{0}}[f(x)-g(x)]=L-M](https://hayhochoi.vn/uploads/news/wyswyg/2020_07/1594183019d3m6g42vv7.gif)
![small lim_{x ightarrow x_{0}}[f(x).g(x)]=L.M](https://hayhochoi.vn/uploads/news/wyswyg/2020_07/1594183021hh7kdqv700.gif)
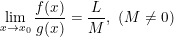
b) Nếu 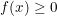 và
và 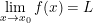 thì:
thì:
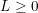 và
và 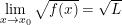
c) Nếu 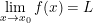 thì
thì 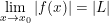
II. Giới hạn vô cực. Giới hạn ở vô cực
1. Giới hạn đặc biệt
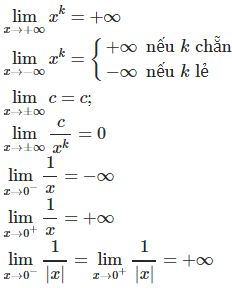
2. Định lý:

III. Giới hạn 1 bên
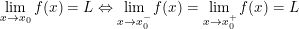
* Khi tính giới hạn có một trong các dạng vô định: 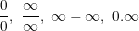 thì phải tìm cách khử dạng vô định.
thì phải tìm cách khử dạng vô định.
* Chú ý: Đối với các hàm lượng giác thì vận dụng tương tự với giới hạn khi x tiến tới vô cùng của sinx/x =1
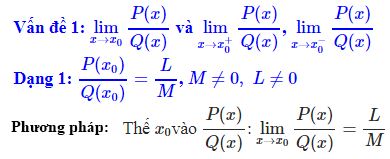
* Ví dụ 1: Tính giới hạn:
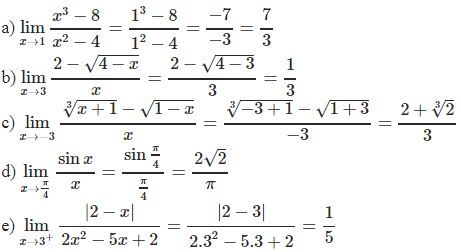
Bài tập vận dụng dạng 1:
¤ Bài tập 1: Tìm các giới hạn sau
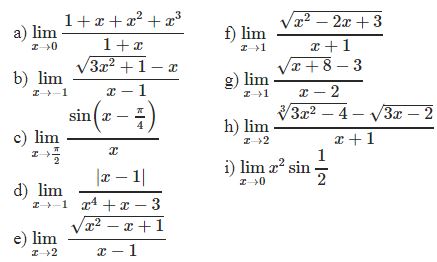
¤ Bài tập 2: Tìm các giới hạn sau
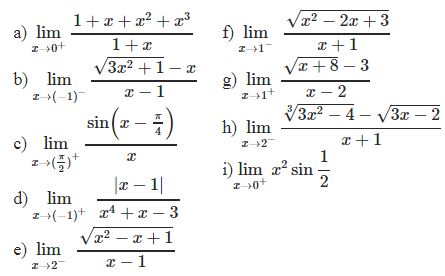
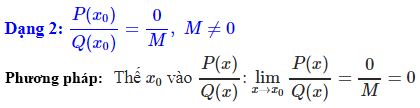
* Ví dụ 2: Tính các giới hạn
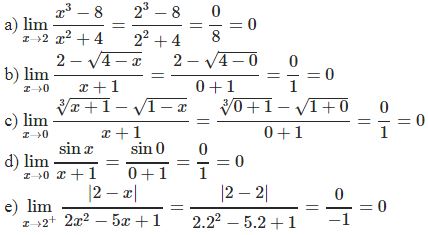
Bài tập vận dụng dạng 2:
¤ Bài tập 1: Tìm các giới hạn sau
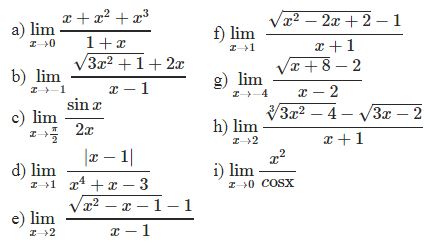
¤ Bài tập 2: Tìm các giới hạn sau
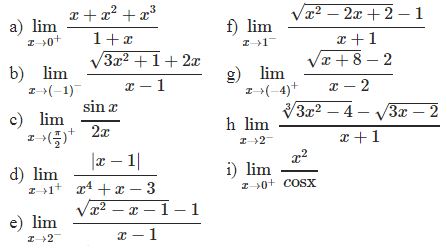
![]()
* Phương pháp: Áp dụng 2 quy tắc giới hạn vô cực (Quy tắc 1 & Quy tắc 2)
* Ví dụ 3: Tính giới hạn
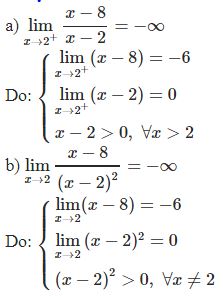
Bài tập vận dụng dạng 3:
¤ Bài tập 1: Tìm các giới hạn sau:
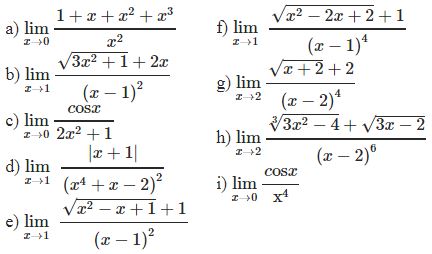
Bài tập 2: Tìm các giới hạn sau:
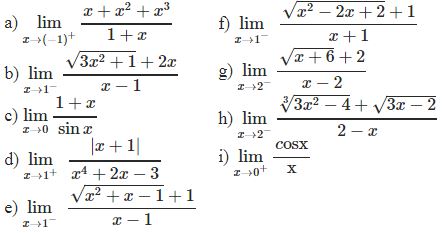
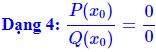
* Phương pháp:
- Nhóm các nhân tử chung: x - x0
- Nhân thêm lượng liên hợp
- Thêm, bớt số hạng vắng.
a) 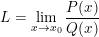 với
với 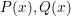 là các đa thức và
là các đa thức và 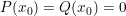
Ta phân tích cả tử và mẫu thành nhân tử và rút gọn.
* Ví dụ 4: Tính giới hạn:
• 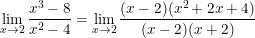
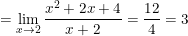
b) 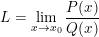 với
với 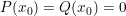 và
và 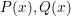 là các biểu thức chứa căn đồng bậc.
là các biểu thức chứa căn đồng bậc.
- Ta sử dụng các hằng đẳng thức để nhân lượng liên hợp ở tử thức và mẫu thức.
* Ví dụ 5: Tính giới hạn:
• 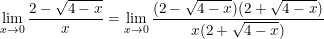
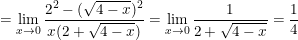
c) 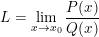 với
với 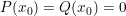 và
và 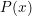 là biểu thức chứa căn không đồng bậc.
là biểu thức chứa căn không đồng bậc.
Giả sử: ![small P(x)=sqrt[m]{u(x)}-sqrt[n]{v(x)}](https://hayhochoi.vn/uploads/news/wyswyg/2020_07/1594195247w6bmyncin3.gif) với
với ![small sqrt[m]{u(x_{0})}-sqrt[n]{v(x_{0})}=a](https://hayhochoi.vn/uploads/news/wyswyg/2020_07/159419221735ygzqj4cl.gif)
Ta phân tích: ![small small P(x)=(sqrt[m]{u(x)}-a)+(a-sqrt[n]{v(x)})](https://hayhochoi.vn/uploads/news/wyswyg/2020_07/1594195248s3pi7hilb4.gif)
* Ví dụ 6: Tìm giới hạn:
•![small lim_{x ightarrow 0}frac{sqrt[3]{x+1}-sqrt{1-x}}{x} =lim_{x ightarrow 0}left (frac{sqrt[3]{x+1}-1}{x}+frac{1-sqrt{1-x}}{x} ight )](https://hayhochoi.vn/uploads/news/wyswyg/2020_07/15941922210zguu2t0ra.gif)
![small =lim_{x ightarrow 0}left (frac{1}{sqrt[3]{(x+1)^2}+sqrt[3]{x+1}+1}+frac{1}{1+sqrt{1-x}} ight )](https://hayhochoi.vn/uploads/news/wyswyg/2020_07/1594192222otwax094qa.gif)
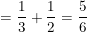
Bài tập vận dụng dạng 4:
¤ Bài tập 1: Tìm các giới hạn sau
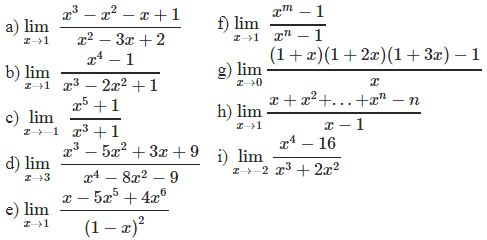
¤ Bài tập 2: Tìm các giới hạn sau
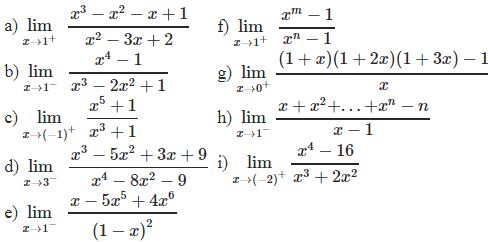
¤ Bài tập 3: Tìm các giới hạn sau
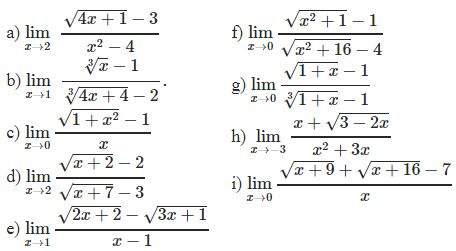
¤ Bài tập 4: Tìm các giới hạn sau
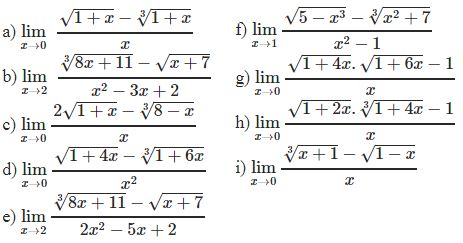
![]()
* Phương pháp: Ta cũng thường sử dụng các phương pháp như các dạng trên
* Ví dụ 7: Tìm giới hạn sau:
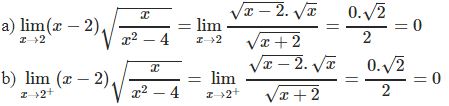
Bài tập vận dụng dạng 5
¤ Bài tập 1: Tìm các giới hạn sau
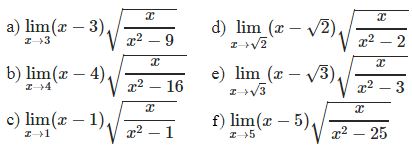
![]()
* Phương pháp: Ta cũng thường sử dụng các phương pháp như các dạng trên
* Ví dụ 8: Tìm giới hạn sau:
•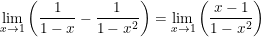
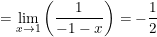
Bài tập vận dụng dạng 6:
¤ Bài tập 1: Tìm các giới hạn sau
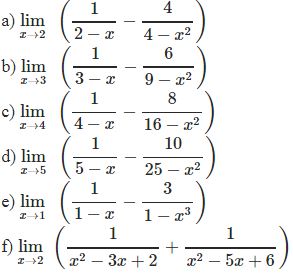
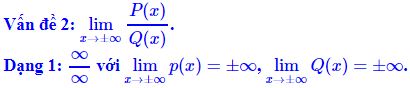
* Phương pháp:
_ Nếu P(x), Q(x) là các đa thức thì chia cả tử và mẫu cho luỹ thừa cao nhất của x
_ Nếu P(x), Q(x) có chứa căn thì có thể chia cả tử và mẫu cho luỹ thừa cao nhất của x hoặc nhân lượng liên hợp.

* Ví dụ 1: Tính các giới hạn sau
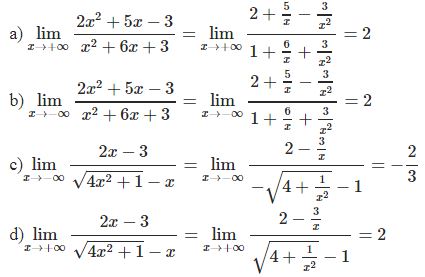
Bài tập vận dụng dạng 1:
¤ Bài tập 1: Tìm các giới hạn sau
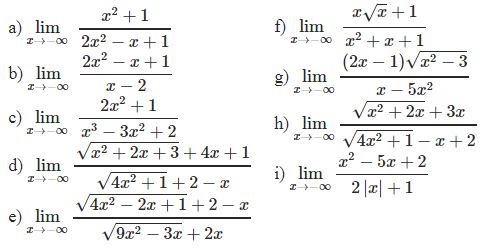
¤ Bài tập 2: Tìm các giới hạn sau
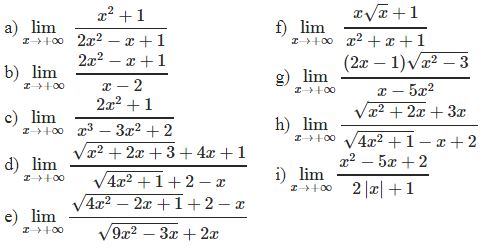

* Phương pháp: Ta thường sử dụng nhân lượng liên hợp cả tử và mẫu
* Ví dụ 2: Tìm các giới hạn
a)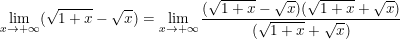
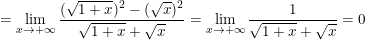
b)![small lim_{x ightarrow -infty }(sqrt[3]{1+x^2-x^3}+x)](https://hayhochoi.vn/uploads/news/wyswyg/2020_07/15941952564z6ge29jhr.gif)
![small =lim_{x ightarrow -infty }frac{1+x^2}{left ( sqrt[3]{1+x^2-x^3} ight )^2-xsqrt[3]{1+x^2-x^3}+x^2}](https://hayhochoi.vn/uploads/news/wyswyg/2020_07/15941952574euypszvmx.gif)
![small =lim_{x ightarrow -infty }frac{frac{1}{x^2}+1}{left ( sqrt[3]{frac{1}{x^3}+frac{1}{x}-1} ight )^2-sqrt[3]{frac{1}{x^3}+frac{1}{x}-1}+1}=frac{1}{3}](https://hayhochoi.vn/uploads/news/wyswyg/2020_07/1594195259mxx47hbwo2.gif)
Bài tập vận dụng dạng 2:
¤ Bài tập 1: Tìm giới hạn sau
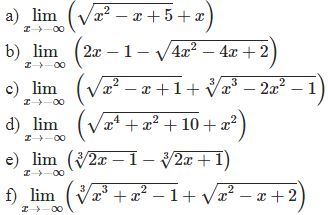
¤ Bài tập 2: Tìm giới hạn sau
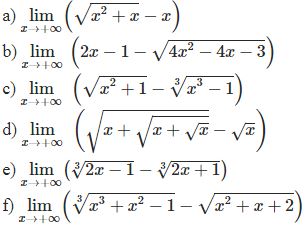

* Phương pháp: Sử dụng tổng hợp các phương pháp trên
* Ví dụ 3: Tìm các giới hạn sau:
a)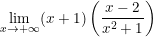
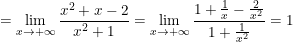
b)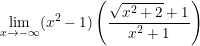
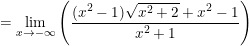
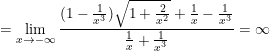
Do: 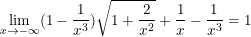 ;
; 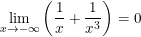
Bài tập vận dụng dạng 3:
¤ Bài tập 1: Tìm giới hạn sau
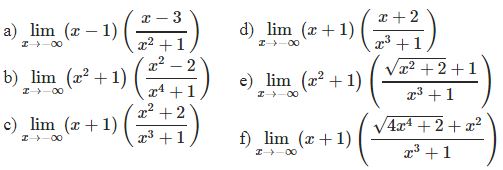
¤ Bài tập 2: Tìm các giới hạn sau
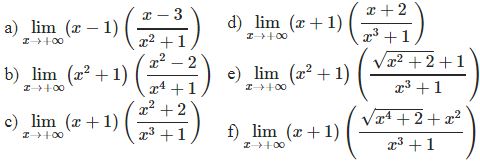
B. Mối quan hệ giữa giới hạn một bên và giới hạn tại một điểm
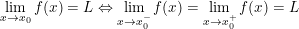
- Sử dụng cách tính giới hạn của hàm số.
* Ví dụ 1: Tìm giới hạn một bên của hàm số tại điểm được chỉ ra:
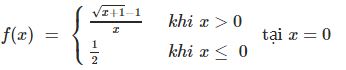
° Hướng dẫn:
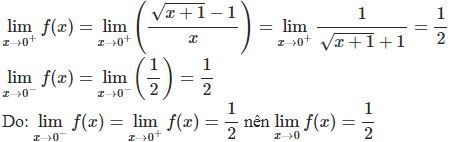
* Ví dụ 2: Tìm giá trị của m để các hàm số sau có giới hạn tại điểm được chỉ ra:
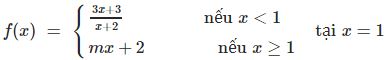
° Hướng dẫn:
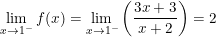
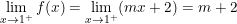
- Để hàm số có giới hạn tại x = 1 thì:
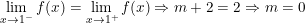
Bài tập vận dụng
¤ Bài tập 1: Tìm các giới hạn một bên của hàm số tại điểm được chỉ ra
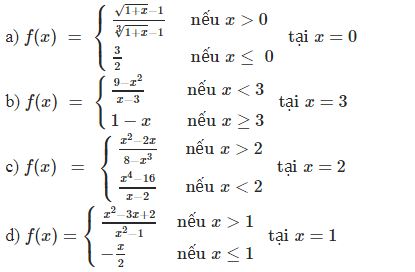
¤ Bài tập 2: Tìm giá trị của m để các hàm số sau có giới tại điểm được chỉ ra
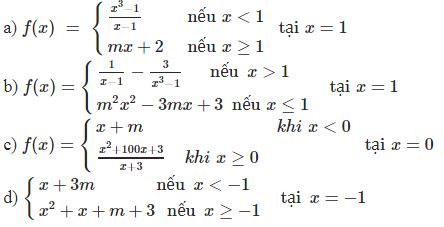
Từ khóa » Các Công Thức đặc Biệt Của Lim
-
Công Thức Tính Lim - Gia Sư Tâm Tài Đức
-
[PDF] Bảng Các Công Thức Tính Giới Hạn Hàm Số - Boxthuthuat
-
Giới Hạn Hàm Số Lớp 11: Lý Thuyết, Công Thức, Bài Tập - Boxthuthuat
-
Lý Thuyết Về Giới Hạn Của Dãy Số | SGK Toán Lớp 11
-
Cách Tính Lim Bằng Tay Của Hàm Số, Bằng Phương Pháp Thủ Công ...
-
Giới Hạn Hàm Số - Cách Xử Lý Các Dạng Vô định
-
Các Giới Hạn đặc Biệt Toán Cao Cấp
-
Giới Hạn Hàm Số Lớp 11: Lý Thuyết, Công Thức Lim ), Công Thức ...
-
Một Số Phương Pháp Tính Giới Hạn (lim) - Theza2
-
Các Công Thức Lượng Giác Toán 10 Đầy Đủ Nhất - Kiến Guru
-
Top 17 Công Thức Giới Hạn Lim - Interconex
-
Các Công Thức Tính Giới Hạn Của Hàm Số Lượng Giác