Toán 12 - Cực Trị Hàm F(|x|) - HOCMAI Forum

• Diễn đàn Bài viết mới Tìm kiếm trên diễn đàn
• Đăng bài nhanh
• Có gì mới? Bài viết mới New media New media comments Status mới Hoạt động mới
• Thư viện ảnh New media New comments Search media
• Story
• Thành viên Đang truy cập Đăng trạng thái mới Tìm kiếm status cá nhân

Đăng nhập Đăng ký

Tìm kiếm

Everywhere Đề tài thảo luận This forum This thread Chỉ tìm trong tiêu đề By: Search Tìm nâng cao… Everywhere Đề tài thảo luận This forum This thread Chỉ tìm trong tiêu đề By: Search Advanced…

• Bài viết mới
• Tìm kiếm trên diễn đàn

Menu Install the app Install Toán 12Cực trị hàm f(|x|)

• Thread starter Tiến Phùng
• Ngày gửi 26 Tháng chín 2019
• Replies 0
• Views 1,390

• Bạn có 1 Tin nhắn và 1 Thông báo mới. [Xem hướng dẫn] để sử dụng diễn đàn tốt hơn trên điện thoại

• Diễn đàn
• TOÁN
• TRUNG HỌC PHỔ THÔNG
• Toán lớp 12
• Ứng dụng đạo hàm

You are using an out of date browser. It may not display this or other websites correctly.You should upgrade or use an alternative browser. T

Tiến Phùng

Cựu Cố vấn Toán

Thành viên 27 Tháng mười 2018 3,742 3,706 561 Hà Nội Trường Đại học Bách Khoa Hà Nội [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Kiến thức cơ bản: Ta có thể dễ dàng thấy hàm y=f(|x|) là một hàm chẵn, do đó 2 nhánh của đồ thị đối xứng nhau qua trục Oy. 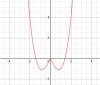Ví dụ ở hình trên là 1 đồ thị của hàm chẵn. Do tính đối xứng như chiếu qua 1 tấm gương, nên ta thấy nhánh đồ thị với x>0 có bao nhiêu cực trị, thì nhánh bên x<0 cũng có bấy nhiêu cực trị. Đồng thời tại x=0(với các hàm liên tục tại x=0) thì đồ thị luôn có một cực trị nữa. (Chỉ trừ trường hợp dạng hàm hằng như y=a, nhưng dạng hàm này không bao giờ gặp với bài toán này) Từ đó ta thấy số cực trị có thể là: nếu với x>0 hàm có a cực trị thì trên toàn khoảng đang xét hàm có 2a+1 cực trị. Bài tập: 1. Cho hàm số: [TEX]y=f(x)=x^3-3x^2-9x+2[/TEX]. Hỏi hàm số [TEX]f(|x|)[/TEX] có bao nhiêu cực trị? Ta có: [TEX]f'(x)=3x^2-6x-9; f'(x)=0<=>x=-1[/TEX] hoặc [TEX]x=3[/TEX] Xét với x>0 thì ta có: PT [TEX]f'(x)=0[/TEX] chỉ có 1 nghiệm x=3. Do đó hàm có 1 cực trị khi x>0 Vậy số cực trị của hàm f(|x|) trên R là: 1.2+1=3 2. Cho hàm số: [TEX]f(x)=x^3-3mx^2+3(m+1)x+1[/TEX]. Tìm m để hàm số f(|x|) có 5 cực trị Giải: Ta có: [TEX]f'(x)=3x^2-6mx+3(m+1)[/TEX]. Xét x>0. Theo lý thuyết đã biết thì hàm f(|x|) có 5 cực trị chỉ khi hàm f(x) có 2 cực trị với x>0. do đó PT [TEX]f'(x)=0<=>3x^2-6mx+3(m+1)=0[/TEX](1) phải có 2 nghiệm phân biệt dương. [TEX](1)<=>x^2-2mx+(m+1)=0[/TEX] Để PT có 2 nghiệm phân biệt dương thì: [tex]\left\{\begin{matrix} \Delta '>0\\ S>0\\ P>0 \end{matrix}\right. <=>\left\{\begin{matrix} m^2-m-1>0\\ 2m>0\\ m+1>0 \end{matrix}\right. <=>m>\frac{1+\sqrt{5}}{2}[/tex] 3. Cho hàm số: [tex]y=f(x)=\frac{x^2-mx+6}{x-1}[/tex]. Tìm m để hàm số [TEX]y=f(|x|)[/TEX] có 5 cực trị. Giải: Điều kiện: [TEX]x \neq 1[/TEX] Ta có: [tex]y'=\frac{x^2-2x+m-6}{(x-1)^2}[/tex] (2) Xét x>0. Để hàm có 5 cực trị thì pt (2) phải có 2 nghiệm phân biệt dương khác 1. Xét điều kiện 2 nghiệm phân biệt dương: [tex]\left\{\begin{matrix} \Delta '>0\\ S>0\\ P>0 \end{matrix}\right. <=>\left\{\begin{matrix} 7-m>0\\ 2>0\\ m-6>0 \end{matrix}\right. <=>6<m<7[/tex] Điều kiện nghiệm khác 1: ta có: [TEX]1-2.1+m-6 \neq 0<=>m \neq 7[/TEX] Vậy kết luận: 6<m<7 là điều kiện cần tìm. Bên dưới là hình minh họa đồ thị với m=6,8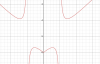

• 

Reactions: Nguyễn Hương Trà You must log in or register to reply here. Chia sẻ: Facebook Reddit Pinterest Tumblr WhatsApp Email Chia sẻ Link

• Diễn đàn
• TOÁN
• TRUNG HỌC PHỔ THÔNG
• Toán lớp 12
• Ứng dụng đạo hàm

Top Bottom

• Vui lòng cài đặt tỷ lệ % hiển thị từ 85-90% ở trình duyệt trên máy tính để sử dụng diễn đàn được tốt hơn.