Toán 12 Ôn Tập Chương 3 Nguyên Hàm, Tích Phân Và Ứng Dụng

YOMEDIA NONE Trang chủ Toán 12 Chương 3: Nguyên Hàm - Tích Phân Và Ứng Dụng Toán 12 Ôn tập chương 3 Nguyên hàm, Tích phân và Ứng dụng ADMICRO Lý thuyết10 Trắc nghiệm58 BT SGK 379 FAQ

Bài ôn tập chương Nguyên hàm - Tích phân và ứng dụng sẽ giúp các em hệ thống lại kiến thức của toàn bộ các bài đã học thông qua các sơ đồ, cùng với đó là các bảng tra cứu nhanh nguyên hàm các hàm số quen thuộc,...sẽ giúp các em ghi nhớ bài học tốt hơn.

ATNETWORK YOMEDIA

1. Video bài giảng

2. Tóm tắt lý thuyết

2.1. Sơ đồ chung các bài toán tích phân và ứng dụng

2.2. Bảng công thức nguyên hàm của một số hàm số

2.3. Dạng nguyên hàm từng phần và cách chọn u, dv

2.4. Dạng nguyên hàm vô tỉ

3. Bài tập minh hoạ

4. Luyện tập Ôn tập Chương 3 Toán 12

4.1. Trắc nghiệm

4.2. Bài tập SGK

5. Hỏi đáp Ôn tập Chương 3 Toán 12

Tóm tắt lý thuyết

2.1. Sơ đồ chung các bài toán tích phân và ứng dụng

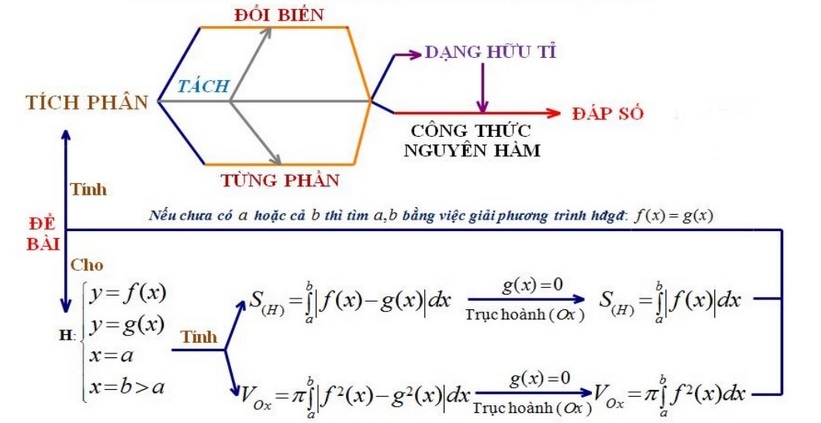
2.2. Bảng công thức nguyên hàm của một số hàm số

2.3. Các dạng nguyên hàm từng phần và cách chọn u, dv

2.4. Các dạng nguyên hàm vô tỉ và các phép đổi biến số lượng giác hóa

Bài tập minh họa

Bài tập 1:

Tìm các nguyên hàm sau:

a) \(I = \int\limits {\left( {3x + 1} \right)\left( {x - 2} \right)} \,dx\).

b) \(J = \int\limits {\left( {5{{\sin }^2}x - \sin x + 2} \right)\cos x} \,dx\).

Lời giải:

a) \(I = \int\limits {\left( {3x + 1} \right)\left( {x - 2} \right)} \,dx\)

\(I = \int\limits {\left( {3{x^2} - 5x - 2} \right)} \,dx = {x^3} - \frac{{5{x^2}}}{2} - 2x + C.\)

b) \(J = \int\limits {\left( {5{{\sin }^2}x - \sin x + 2} \right)\cos x} \,dx\)

Đặt: \(t = \sin x \Rightarrow dt = \cos xdx\)

Khi đó: \(J = \int\limits {\left( {5{t^2} - t + 2} \right)} \,dt = \frac{{5{t^3}}}{3} - \frac{{{t^2}}}{2} + 2t + C = \frac{5}{3}{\sin ^3}x - \frac{{{{\sin }^2}x}}{2} + 2\sin x + C.\)

Bài tập 2:

Tính các tích phân sau:

a) \(I=\int_{1}^{3}x(3x+2lnx)dx.\)

b) \(I=\int_{1}^{2}\frac{x^2+ln^2x}{x}dx.\)

c) \(I = \int\limits_{\frac{{\sqrt 2 }}{2}}^1 {\frac{{\sqrt {1 - {x^2}} }}{{{x^2}}}dx} .\)

Lời giải:

a) \(I=\int_{1}^{2}3x^2dx+\int_{1}^{2}2xlnxdx\) Đặt \(I_1=\int_{1}^{2}3x^2dx; I_2=\int_{1}^{2}2xlnxdx\) \(I_1=\int_{1}^{2}3x^2dx=x^3\bigg |^2_1=7.\) \(I_2=\int_{1}^{2}lnxd(x^2)=(x^2lnx)\bigg|^2_1-\int_{1}^{2}xdx=4ln2- \frac{x^2}{2}\bigg|^2_1=4ln2-\frac{3}{2}.\) Vậy \(I=I_1+I_2=4ln2-\frac{11}{2}.\)

b) Ta tách tích phân I như sau: \(I=\int_{1}^{2}\frac{x^2+ln^2x}{x}dx=\int_{1}^{2}xdx+\int_{1}^{2}\frac{ln^2x}{x}dx\) \(I_1=\int_{1}^{2}xdx=\frac{x^2}{2}\bigg|^2_1=\frac{3}{2}\) \(I_2=\int_{1}^{2}\frac{ln^2x}{x}dx\) Đặt \(t=lnx\Rightarrow dt=\frac{1}{x}dx\) Đổi cận: \(x=2\Rightarrow t=ln2;x=1\Rightarrow t=0\) \(I_2=\int_{0}^{ln2}t^2dt=\frac{t^3}{3}\bigg |^{ln2}_0=\frac{ln^32}{3}\) Vậy \(I=I_1+I_2=\frac{3}{2}+\frac{ln^32}{3}.\)

c) \(I = \int\limits_{\frac{{\sqrt 2 }}{2}}^1 {\frac{{\sqrt {1 - {x^2}} }}{{{x^2}}}dx} .\)

Đặt \(x = \cos t,t \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right] \Rightarrow dx = - \sin tdt\)

Đổi cận: \(\left\{ \begin{array}{l} x = \frac{{\sqrt 2 }}{2} \Rightarrow t = \frac{\pi }{4}\\ x = 1 \Rightarrow t = 0 \end{array} \right.\)

Khi đó:

\(\begin{array}{l} I = - \int\limits_{\frac{\pi }{4}}^0 {\frac{{\sqrt {1 - {{\cos }^2}t} .\sin t}}{{{{\cos }^2}t}}dt} = \int\limits_0^{\frac{\pi }{4}} {\frac{{\left| {\sin t} \right|.\sin t}}{{{{\cos }^2}t}}dt} \\ = \int\limits_0^{\frac{\pi }{4}} {\left( {\frac{1}{{{{\cos }^2}t}} - 1} \right)dt} = \left. {\left( {\tan t - t} \right)} \right|_0^{\frac{\pi }{4}} = 1 - \frac{\pi }{4}. \end{array}\)

Bài tập 3:

Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x2 + x, trục hoành và hai đường thẳng x = 0, x = 1.

Lời giải:

Diện tích hình phẳng cần tính là: \(S=\int_{0}^{1}\left | x^2+x \right |dx\) Với \(x\in [0;1]\Rightarrow S=\int_{0}^{1}(x^2+x)dx\) Suy ra \(S=(\frac{x^3}{3}+\frac{x^2}{2})\bigg |^1_0=\frac{5}{6}.\) Vậy \(S=\frac{5}{6}\).

Bài tập 4:

Cho hình phẳng giới hạn bởi các đường \(y = \frac{1}{{1 + \sqrt {4 - 3{\rm{x}}} }},y = 0,x = 0,x = 1\) quay quanh trục Ox. Tính thể tích V của khối tròn xoay tạo thành.

Lời giải:

Thể tích cần tìm: \(V = \pi \int\limits_0^1 {\frac{{dx}}{{{{\left( {1 + \sqrt {4 - 3x} } \right)}^2}}}}\)

Đặt:\(t = \sqrt {4 - 3x} \Rightarrow dt = - \frac{3}{{2\sqrt {4 - 3x} }}dx \Leftrightarrow dx = - \frac{2}{3}tdt\left( {x = 0 \Rightarrow t = 2;x = 1 \Rightarrow t = 1} \right)\)

Khi đó:

\(\begin{array}{l} V = \frac{{2\pi }}{3}\int\limits_1^2 {\frac{t}{{{{\left( {1 + t} \right)}^2}}}dt} = \frac{{2\pi }}{3}\int\limits_1^2 {\left( {\frac{1}{{1 + t}} - \frac{1}{{{{\left( {1 + t} \right)}^2}}}} \right)dt} \\ = \left. {\frac{{2\pi }}{3}\left( {\ln \left| {1 + t} \right| + \frac{1}{{1 + t}}} \right)} \right|_1^2 = \frac{\pi }{9}\left( {6\ln \frac{3}{2} - 1} \right). \end{array}\)

4. Luyện tập Ôn tập Chương 3 Toán 12

Bài ôn tập chương Nguyên hàm - Tích phân và ứng dụng sẽ giúp các em hệ thống lại kiến thức của toàn bộ các bài đã học thông qua các sơ đồ, cùng với đó là các bảng tra cứu nhanh nguyên hàm các hàm số quen thuộc,...sẽ giúp các em ghi nhớ bài học tốt hơn.

4.1 Trắc nghiệm

Để cùng cố bài học xin mời các em củng làm Bài kiểm tra Trắc nghiệm Toán 12 Ôn tập chương 3 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.

• Câu 1:

  Hàm số nào sau đây không phải làm nguyên hàm của hàm số \(f(x) = 2\sin 2x.\)

  • A. \(F(x) = 2{\sin ^2}x\)
  • B. \(F(x) = - 2{\cos ^2}x\)
  • C. \(F(x) = - 1 - \cos 2x\)
  • D. \(F(x) = - 1 - 2\cos x\sin x\)

• Câu 2:

  Biết \(F\left( x \right) = \left( {ax + b} \right).{e^x}\) là nguyên hàm của hàm số \(y = \left( {2x + 3} \right).{e^x}.\) Tính tổng a + b.

  • A. a+b=2
  • B. a+b=3
  • C. a+b=4
  • D. a+b=5

• Câu 3:

  Trong các tích phân sau, tích phân nào không có cùng giá trị với \(I = \int\limits_1^2 {{x^3}\sqrt {{x^2} - 1} dx} .\)

  • A. \(\frac{1}{2}\int_1^2 {t\sqrt {t - 1} dt}\)
  • B. \(\frac{1}{2}\int_1^4 {t\sqrt {t - 1} dt}\)
  • C. \(\int_0^{\sqrt 3 } {\left( {{t^2} + 1} \right){t^2}dt}\)
  • D. \(\int_0^{\sqrt 3 } {\left( {{x^2} + 1} \right){x^2}dx}\)

Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!

4.2 Bài tập SGK

Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Toán 12 Ôn tập chương 3 sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK Giải tích 12 Cơ bản và Nâng cao.

Bài tập 1 trang 126 SGK Giải tích 12

Bài tập 2 trang 126 SGK Giải tích 12

Bài tập 3 trang 126 SGK Giải tích 12

Bài tập 4 trang 126 SGK Giải tích 12

Bài tập 5 trang 127 SGK Giải tích 12

Bài tập 6 trang 127 SGK Giải tích 12

Bài tập 7 trang 127 SGK Giải tích 12

Bài tập 1 trang 128 SGK Giải tích 12

Bài tập 2 trang 128 SGK Giải tích 12

Bài tập 3 trang 128 SGK Giải tích 12

Bài tập 4 trang 128 SGK Giải tích 12

Bài tập 5 trang 128 SGK Giải tích 12

Bài tập 6 trang 128 SGK Giải tích 12

Bài tập 41 trang 175 SGK Toán 12 NC

Bài tập 42 trang 175 SGK Toán 12 NC

Bài tập 43 trang 176 SGK Toán 12 NC

Bài tập 44 trang 176 SGK Toán 12 NC

Bài tập 45 trang 176 SGK Toán 12 NC

Bài tập 46 trang 176 SGK Toán 12 NC

Bài tập 47 trang 176 SGK Toán 12 NC

Bài tập 48 trang 176 SGK Toán 12 NC

Bài tập 49 trang 176 SGK Toán 12 NC

Bài tập 50 trang 176 SGK Toán 12 NC

Bài tập 51 trang 176 SGK Toán 12 NC

Bài tập 52 trang 177 SGK Toán 12 NC

Bài tập 53 trang 177 SGK Toán 12 NC

Bài tập 54 trang 177 SGK Toán 12 NC

Bài tập 55 trang 177 SGK Toán 12 NC

Bài tập 56 trang 177 SGK Toán 12 NC

Bài tập 57 trang 177 SGK Toán 12 NC

Bài tập 58 trang 177 SGK Toán 12 NC

Bài tập 59 trang 177 SGK Toán 12 NC

Bài tập 60 trang 178 SGK Toán 12 NC

Bài tập 61 trang 178 SGK Toán 12 NC

Bài tập 62 trang 178 SGK Toán 12 NC

Bài tập 63 trang 178 SGK Toán 12 NC

Bài tập 64 trang 178 SGK Toán 12 NC

Bài tập 65 trang 178 SGK Toán 12 NC

Bài tập 66 trang 179 SGK Toán 12 NC

Bài tập 67 trang 179 SGK Toán 12 NC

Bài tập 3.43 trang 180 SBT Toán 12

Bài tập 3.44 trang 180 SBT Toán 12

Bài tập 3.45 trang 181 SBT Toán 12

Bài tập 3.46 trang 181 SBT Toán 12

Bài tập 3.47 trang 181 SBT Toán 12

Bài tập 3.48 trang 181 SBT Toán 12

Bài tập 3.49 trang 182 SBT Toán 12

Bài tập 3.50 trang 182 SBT Toán 12

Bài tập 3.51 trang 182 SBT Toán 12

Bài tập 3.52 trang 182 SBT Toán 12

Bài tập 3.53 trang 183 SBT Toán 12

Bài tập 3.54 trang 183 SBT Toán 12

Bài tập 3.55 trang 183 SBT Toán 12

Bài tập 3.56 trang 183 SBT Toán 12

Bài tập 3.67 trang 183 SBT Toán 12

Bài tập 3.58 trang 184 SBT Toán 12

Bài tập 3.59 trang 184 SBT Toán 12

Bài tập 3.60 trang 184 SBT Toán 12

5. Hỏi đáp về Ôn tập Chương 3 Toán 12

Nếu có thắc mắc cần giải đáp các em có thể để lại câu hỏi trong phần Hỏi đáp, cộng đồng Toán HỌC247 sẽ sớm trả lời cho các em.

-- Mod Toán Học 12 HỌC247

NONE

Bài học cùng chương

Toán 12 Bài 1: Nguyên hàm Toán 12 Bài 2: Tích phân Toán 12 Bài 3: Ứng dụng của tích phân trong hình học ADSENSE TRACNGHIEM Bộ đề thi nổi bật UREKA AANETWORK

XEM NHANH CHƯƠNG TRÌNH LỚP 12

Toán 12

Lý thuyết Toán 12

Giải bài tập SGK Toán 12

Giải BT sách nâng cao Toán 12

Trắc nghiệm Toán 12

Hình học 12 Chương 3

Ngữ văn 12

Lý thuyết Ngữ Văn 12

Soạn văn 12

Soạn văn 12 (ngắn gọn)

Văn mẫu 12

Soạn Ai đã đặt tên cho dòng sông

Tiếng Anh 12

Giải bài Tiếng Anh 12

Giải bài Tiếng Anh 12 (Mới)

Trắc nghiệm Tiếng Anh 12

Unit 9 Lớp 12 Deserts

Tiếng Anh 12 mới Unit 4

Vật lý 12

Lý thuyết Vật Lý 12

Giải bài tập SGK Vật Lý 12

Giải BT sách nâng cao Vật Lý 12

Trắc nghiệm Vật Lý 12

Ôn tập Vật lý 12 Chương 3

Hoá học 12

Lý thuyết Hóa 12

Giải bài tập SGK Hóa 12

Giải BT sách nâng cao Hóa 12

Trắc nghiệm Hóa 12

Ôn tập Hóa học 12 Chương 4

Sinh học 12

Lý thuyết Sinh 12

Giải bài tập SGK Sinh 12

Giải BT sách nâng cao Sinh 12

Trắc nghiệm Sinh 12

Ôn tập Sinh 12 Chương 1 - Tiến hóa

Lịch sử 12

Lý thuyết Lịch sử 12

Giải bài tập SGK Lịch sử 12

Trắc nghiệm Lịch sử 12

Lịch Sử 12 Chương 2 Lịch Sử VN

Địa lý 12

Lý thuyết Địa lý 12

Giải bài tập SGK Địa lý 12

Trắc nghiệm Địa lý 12

Địa Lý 12 VĐSD và BVTN

GDCD 12

Lý thuyết GDCD 12

Giải bài tập SGK GDCD 12

Trắc nghiệm GDCD 12

GDCD 12 Học kì 1

Công nghệ 12

Lý thuyết Công nghệ 12

Giải bài tập SGK Công nghệ 12

Trắc nghiệm Công nghệ 12

Công nghệ 12 Chương 3

Tin học 12

Lý thuyết Tin học 12

Giải bài tập SGK Tin học 12

Trắc nghiệm Tin học 12

Tin học 12 Chương 2

Cộng đồng

Hỏi đáp lớp 12

Tư liệu lớp 12

Xem nhiều nhất tuần

Video: Vợ nhặt của Kim Lân

Đề cương HK1 lớp 12

Video ôn thi THPT QG môn Toán

Video ôn thi THPT QG môn Văn

Video ôn thi THPT QG môn Sinh

Video ôn thi THPT QG môn Vật lý

Video ôn thi THPT QG Tiếng Anh

Video ôn thi THPT QG môn Hóa

Quá trình văn học và phong cách văn học

Khái quát văn học Việt Nam từ đầu CMT8 1945 đến thế kỉ XX

Người lái đò sông Đà

Đất Nước- Nguyễn Khoa Điềm

Đàn ghi ta của Lor-ca

Tây Tiến

Ai đã đặt tên cho dòng sông

YOMEDIA YOMEDIA ×

Thông báo

Bạn vui lòng đăng nhập trước khi sử dụng chức năng này.

Bỏ qua Đăng nhập ×

Thông báo

Bạn vui lòng đăng nhập trước khi sử dụng chức năng này.

Đồng ý ATNETWORK ON QC Bỏ qua >>