Toán 7 Bài 7: Đồ Thị Của Hàm Số Y = Ax (a ≠ 0) - HOC247

YOMEDIA NONE Trang chủ Toán 7 Chương 2: Hàm Số Và Đồ Thị Toán 7 Bài 7: Đồ thị của hàm số y = ax (a ≠ 0) ADMICRO Lý thuyết10 Trắc nghiệm23 BT SGK 316 FAQ

Nội dung bài học sẽ giới thiệu đến các em dạng đầu tiên và cơ bản nhất của đồ thị hàm số ở chương trình Toán phổ thông là Đồ thị của hàm số y=ax (a≠0). Cùng với những bài tập minh họa có hướng dẫn giải, sẽ giúp các em dễ dàng nắm được các tính chất và dạng toán liên quan đến đồ thị hàm số này.

ATNETWORK YOMEDIA

1. Tóm tắt lý thuyết

1.1. Đồ thị của hàm số

1.2. Đồ thị của hàm số \(y = {\rm{ax(a}} \ne {\rm{0)}}\)

2. Bài tập minh hoạ

3. Luyện tập Bài 7 Chương 2 Đại số 7

3.1 Trắc nghiệm về Đồ thị của hàm số y = ax (a ≠ 0)

3.2. Bài tập SGK về Đồ thị của hàm số y = ax (a ≠ 0)

4. Hỏi đáp Bài 7 Chương 2 Đại số 7

Tóm tắt lý thuyết

1.1. Đồ thị của hàm số

Đồ thị của hàm số \(y=f(x)\) là tập hợp tất cả các điểm biểu diễn các cặp giá trị tương ứng (x;y) trên mặt phẳng toạ độ.

1.2. Đồ thị của hàm số \(y = {\rm{ax(a}} \ne {\rm{0)}}\)

• Đồ thị của hàm số \(y = {\rm{ax}}\,\,\,{\rm{(a}} \ne {\rm{0)}}\) là một đường thẳng đi qua gốc toạ độ.

Trường hợp: a>0

Trường hợp: a<0

• Vì đồ thị của hàm số y = ax là một đường thẳng đi qua gốc toạ độ nên ta chỉ cần xác định thêm một điểm A (thường cho x=1; y=a) khác điểm gốc O. Vẽ đường thẳng OA ta được đồ thị của hàm số y = ax.

Ví dụ 1:

Xác định hệ số a của hàm số y = ax trong mỗi trường hợp sau:

a. Đồ thị của hàm số đi qua điểm A(1;3).

b. Đồ thị của hàm số đi qua điểm B(-2;1).

Cho biết hàm số trong mỗi trường hợp trên đi qua góc phần tư nào của hệ trục toạ độ, tại sao?

Hướng dẫn giải:

a. Hàm số đi qua điểm A(1;3) nên ta có:

\(3 = a.1 \Rightarrow a = 3\)

Vậy \(y =3x\).

b. Tương tự hàm số đi qua điểm B(-2; 1), ta có:

\( - 2 = a.1 \Rightarrow a = - \frac{1}{2}\)

Vậy \(y = - \frac{1}{2}\).

Đồ thị hàm số y=3x qua góc phần tư I và III (vì hai toạ độ cùng dấu (cùng dương, cùng âm)).

Đồ thị hàm số \(y = - \frac{1}{2}x\) qua góc phần tư II và IV (vì hai toạ độ trái dấu).

Ví dụ 2:

Vẽ đồ thị của hàm số \(y = \left\{ \begin{array}{l}3x\,\,\,voi\,\,\,x \ge 0\\ - \frac{1}{3}x\,\,voi\,\,x < 0\end{array} \right.\)

Hướng dẫn giải:

• Với \(x \ge 0\):

Cho x=0 được \(y = 0 \Rightarrow O(0;0)\) thuộc đồ thị

Cho x=1 được \(y = 3 \Rightarrow A(1;3)\) thuộc đồ thị

• Với \(x < 0\):

Cho x=-1 được \(y = \frac{1}{3} \Rightarrow B\left( { - 1;\frac{1}{3}} \right)\) thuộc đồ thị

Cho x=-3 được \(y = 1 \Rightarrow C( - 3;1)\) thuộc đồ thị

Vẽ đồ thị: Nối A, O,B, C ta được đồ thị là đường gấp khúc AOC.

Bài tập minh họa

Bài 1:

Cho hình vẽ bên, điểm M có tọa độ \(M\left( {{x_0};{y_0}} \right)\) với \({x_0},{y_0} \in Q.\) Hãy tính tỉ số \(\frac{{{y_0} + 3}}{{{x_0} - 2}}.\)

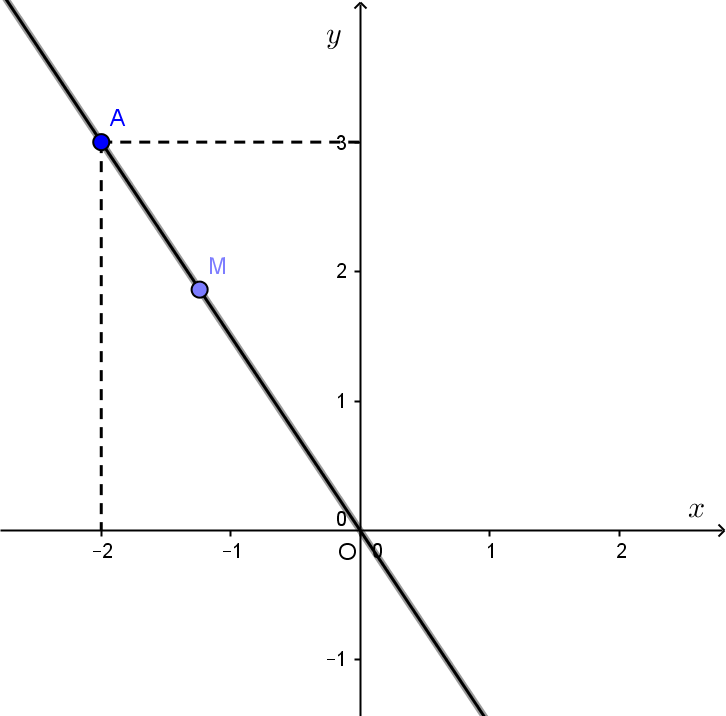
Hướng dẫn giải:

Đường thẳng OA chứa đồ thị hàm số y=ax điểm A(-2;3) thuộc đồ thị hàm số đó nên ta có 3=-2a, suy ra \(a = - \frac{3}{2}.\)

Vậy hàm số được cho bởi công thức \(y = - \frac{3}{2}x.\)

M và A là hai điểm thuộc đồ thị của hàm số nên hoành độ và tung độ của chúng là những đại lượng tỉ lệ thuận, từ đó ta có:

\(\frac{{{y_0}}}{{{x_0}}} = \frac{3}{{ - 2}} = \frac{{{y_0} + 3}}{{{x_0} - 2}}\)

Vậy \(\frac{{{y_0} + 3}}{{{x_0} - 2}} = - \frac{3}{2}\).

Bài 2:

a. Vẽ đồ thị hàm số \(y = \frac{1}{3}x\).

b. Gọi A là điểm trên đồ thị. Tìm toạ độ điểm A, biết \({y_A} = 2.\)

c. Gọi B là điểm trên đồ thị. Tìm toạ độ điểm B biết \({y_B} + 2{x_B} = 5\).

Hướng dẫn giải:

a. Đồ thị hàm số \(y = \frac{1}{3}x\) đi qua hai điểm O(0;0) và C(3;1).

b. A là điểm trên đồ thị nên \({y_A} = \frac{1}{3}{x_A}\) mà \({y_A} = 2\) nên \(2 = \frac{1}{3}{x_A} \Rightarrow {x_A} = 6\)

Vậy A(6;2).

c. B là điểm trên đồ thị nên \({y_B} = \frac{1}{3}{x_B}\) mà \({y_B} + 2{x_B} = 5\)

Nên \(\frac{1}{3}{x_B} + 2{x_B} = 5 \Rightarrow \frac{7}{3}{x_B} = 5\).

\( \Rightarrow {x_B} = \frac{{15}}{7}\) và \({y_B} = \frac{1}{3}.\frac{{15}}{7} = \frac{5}{7}\)

Vậy \(B\left( {\frac{{15}}{7};\frac{5}{7}} \right)\).

Bài 3:

Cho hàm số y=f(x) thoả mãn:

a. f(0)=0.

b. \(\frac{{f({x_1})}}{{{x_1}}} = \frac{{f({x_2})}}{{{x_2}}}\) với \({x_1},{x_2} \in R\).

Chứng minh rằng f(x)=ax với a là hằng số.

Hướng dẫn giải:

Giả sử ta có f(x)=ax với a là hằng số. Cho x=1 ta được f(1)=a. Nên ta đặt a=f(1). Ta chứng minh rằng f(x)=ax với mọi số thực x.

Thật vậy:

• Nếu x=0 thì theo giả thiết:

f(0)=0=a.0

• Nếu \(x \ne 0\) thì theo giả thiết ta có \(\frac{{f(x)}}{x} = \frac{{f(1)}}{1} = a\)

Suy ra f(x)=ax

Vậy f(x)=ax với mọi \(x \in R.\)

3. Luyện tập Bài 7 Chương 2 Đại số 7

Qua bài giảng Đồ thị của hàm số y = ax (a ≠ 0)này, các em cần hoàn thành 1 số mục tiêu mà bài đưa ra như :

• Khái niệm đồ thị hàm số
• Cách vẽ đồ thị hàm số y = ax (a ≠ 0)

3.1 Trắc nghiệm về Đồ thị của hàm số y = ax (a ≠ 0)

Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Toán 7 Bài 7 cực hay có đáp án và lời giải chi tiết.

• Câu 1:

  Điểm thuộc đồ thị hàm số y = -2x là:

  • A. M(-2; -2)
  • B. N(1; 4)
  • C. P(-1; -2)
  • D. Q(-1; 2)

• Câu 2:

  Đồ thị hàm số y = -5x không đi qua điểm

  • A. M(1; 5)
  • B. N(-2; 10)
  • C. P(-1; 5)
  • D. Q(-2; 10)

• Câu 3:

  Điểm B(-2; 6) không thuộc đồ thị hàm số:

  • A. y = -3x
  • B. y = x + 8
  • C. y = 4 -x
  • D. y = x2

Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!

3.2. Bài tập SGK về Đồ thị của hàm số y = ax (a ≠ 0)

Các em có thể xem thêm phần hướng dẫn Giải bài tập Toán 7 Bài 7 để giúp các em nắm vững bài học và các phương pháp giải bài tập.

Bài tập 39 trang 71 SGK Toán 7 Tập 1

Bài tập 40 trang 71 SGK Toán 7 Tập 1

Bài tập 41 trang 72 SGK Toán 7 Tập 1

Bài tập 42 trang 72 SGK Toán 7 Tập 1

Bài tập 43 trang 72 SGK Toán 7 Tập 1

Bài tập 44 trang 73 SGK Toán 7 Tập 1

Bài tập 45 trang 73 SGK Toán 7 Tập 1

Bài tập 46 trang 73 SGK Toán 7 Tập 1

Bài tập 47 trang 73 SGK Toán 7 Tập 1

Bài tập 53 trang 77 SBT Toán 7 Tập 1

Bài tập 54 trang 77 SBT Toán 7 Tập 1

Bài tập 55 trang 77 SBT Toán 7 Tập 1

Bài tập 56 trang 77 SBT Toán 7 Tập 1

Bài tập 56 trang 79 SBT Toán 7 Tập 1

Bài tập 57 trang 79 SBT Toán 7 Tập 1

Bài tập 58 trang 80 SBT Toán 7 Tập 1

Bài tập 59 trang 80 SBT Toán 7 Tập 1

Bài tập 60 trang 80 SBT Toán 7 Tập 1

Bài tập 61 trang 81 SBT Toán 7 Tập 1

Bài tập 7.1 trang 78 SBT Toán 7 Tập 1

Bài tập 7.2 trang 78 SBT Toán 7 Tập 1

Bài tập 7.3 trang 78 SBT Toán 7 Tập 1

Bài tập 7.4 trang 78 SBT Toán 7 Tập 1

4. Hỏi đáp Bài 7 Chương 2 Đại số 7

Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!

Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!

-- Mod Toán Học 7 HỌC247

NONE

Bài học cùng chương

Toán 7 Bài 1: Đại lượng tỉ tệ thuận Toán 7 Bài 2: Một số bài toán về đại lượng tỉ lệ thuận Toán 7 Bài 3: Đại lượng tỉ lệ nghịch Toán 7 Bài 4: Một số bài toán về đại lượng tỉ lệ nghịch Toán 7 Bài 5: Hàm số Toán 7 Bài 6: Mặt phẳng tọa độ ADSENSE ADMICRO Bộ đề thi nổi bật UREKA AANETWORK

XEM NHANH CHƯƠNG TRÌNH LỚP 7

Toán 7

Toán 7 Kết Nối Tri Thức

Toán 7 Chân Trời Sáng Tạo

Toán 7 Cánh Diều

Giải bài tập Toán 7 KNTT

Giải bài tập Toán 7 CTST

Giải bài tập Toán 7 Cánh Diều

Trắc nghiệm Toán 7

Ngữ văn 7

Ngữ Văn 7 Kết Nối Tri Thức

Ngữ Văn 7 Chân Trời Sáng Tạo

Ngữ Văn 7 Cánh Diều

Soạn Văn 7 Kết Nối Tri Thức

Soạn Văn 7 Chân Trời Sáng Tạo

Soạn Văn 7 Cánh Diều

Văn mẫu 7

Tiếng Anh 7

Tiếng Anh 7 Kết Nối Tri Thức

Tiếng Anh 7 Chân Trời Sáng Tạo

Tiếng Anh 7 Cánh Diều

Trắc nghiệm Tiếng Anh 7 KNTT

Trắc nghiệm Tiếng Anh 7 CTST

Trắc nghiệm Tiếng Anh 7 Cánh Diều

Giải Sách bài tập Tiếng Anh 7

Khoa học tự nhiên 7

Khoa học tự nhiên 7 KNTT

Khoa học tự nhiên 7 CTST

Khoa học tự nhiên 7 Cánh Diều

Giải bài tập KHTN 7 KNTT

Giải bài tập KHTN 7 CTST

Giải bài tập KHTN 7 Cánh Diều

Trắc nghiệm Khoa học tự nhiên 7

Lịch sử và Địa lý 7

Lịch sử & Địa lí 7 KNTT

Lịch sử & Địa lí 7 CTST

Lịch sử & Địa lí 7 Cánh Diều

Giải bài tập LS và ĐL 7 KNTT

Giải bài tập LS và ĐL 7 CTST

Giải bài tập LS và ĐL 7 Cánh Diều

Trắc nghiệm Lịch sử và Địa lí 7

GDCD 7

GDCD 7 Kết Nối Tri Thức

GDCD 7 Chân Trời Sáng Tạo

GDCD 7 Cánh Diều

Giải bài tập GDCD 7 KNTT

Giải bài tập GDCD 7 CTST

Giải bài tập GDCD 7 Cánh Diều

Trắc nghiệm GDCD 7

Công nghệ 7

Công nghệ 7 Kết Nối Tri Thức

Công nghệ 7 Chân Trời Sáng Tạo

Công nghệ 7 Cánh Diều

Giải bài tập Công nghệ 7 KNTT

Giải bài tập Công nghệ 7 CTST

Giải bài tập Công nghệ 7 Cánh Diều

Trắc nghiệm Công nghệ 7

Tin học 7

Tin học 7 Kết Nối Tri Thức

Tin học 7 Chân Trời Sáng Tạo

Tin học 7 Cánh Diều

Giải bài tập Tin học 7 KNTT

Giải bài tập Tin học 7 CTST

Giải bài tập Tin học 7 Cánh Diều

Trắc nghiệm Tin học 7

Cộng đồng

Hỏi đáp lớp 7

Tư liệu lớp 7

Xem nhiều nhất tuần

Video Toán nâng cao lớp 7

Đề cương HK1 lớp 7

Tiếng gà trưa - Xuân Quỳnh - Ngữ văn 7 Cánh Diều

Quê hương - Tế Hanh - Ngữ văn 7 Kết Nối Tri Thức

Con chim chiền chiện - Huy Cận - Ngữ văn 7 Chân Trời Sáng Tạo

Toán 7 CTST Bài 2: Các phép tính với số hữu tỉ

Toán 7 Cánh diều Bài tập cuối chương 1

Toán 7 KNTT Bài 1: Tập hợp các số hữu tỉ

YOMEDIA YOMEDIA ×

Thông báo

Bạn vui lòng đăng nhập trước khi sử dụng chức năng này.

Bỏ qua Đăng nhập ×

Thông báo

Bạn vui lòng đăng nhập trước khi sử dụng chức năng này.

Đồng ý ATNETWORK ON QC Bỏ qua >>