Toán 8: Định Lý Talet Trong Tam Giác, Trong Hình Thang
Có thể bạn quan tâm
-
-

-
Mầm non
-
Lớp 1
-
Lớp 2
-
Lớp 3
-
Lớp 4
-
Lớp 5
-
Lớp 6
-
Lớp 7
-
Lớp 8
-
Lớp 9
-
Lớp 10
-
Lớp 11
-
Lớp 12
-
Thi vào lớp 6
-
Thi vào lớp 10
-
Thi Tốt Nghiệp THPT
-
Đánh Giá Năng Lực
-
Khóa Học Trực Tuyến
-
Hỏi bài
-
Trắc nghiệm Online
-
Tiếng Anh
-
Thư viện Học liệu
-
Bài tập Cuối tuần
-
Bài tập Hàng ngày
-
Thư viện Đề thi
-
Giáo án - Bài giảng
-
Tất cả danh mục
-
- Mầm non
- Lớp 1
- Lớp 2
- Lớp 3
- Lớp 4
- Lớp 5
- Lớp 6
- Lớp 7
- Lớp 8
- Lớp 9
- Lớp 10
- Lớp 11
- Lớp 12
- Thi Chuyển Cấp
-
- Hôm nay +3
- Ngày 2 +3
- Ngày 3 +3
- Ngày 4 +3
- Ngày 5 +3
- Ngày 6 +3
- Ngày 7 +5
Toán 8: Định lý Thales trong tam giác
- A. Tỉ số hai đoạn thẳng
- B. Định lý Thales trong tam giác
- 1. Định lý Thales thuận trong tam giác
- 2. Định lý Thales đảo
- 3. Hệ quả của định lí Thales
- C. Bài tập tự luyện
- 1. Câu hỏi trắc nghiệm
- 2. Câu hỏi tự luận
Định lý Talet trong tam giác, trong hình thang cung cấp các phần nội dung quan trọng giúp các em học sinh nắm vững kiến thức để giải các bài toán. Bài viết dưới đây sẽ giúp bạn tổng hợp những kiến thức hữu ích về chủ đề định lý talet, mời các bạn tham khảo để có thể vận dụng vào giải các bài tập Toán liên quan.
A. Tỉ số hai đoạn thẳng
– Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.
Tỉ số của hai đoạn thẳng AB và CD được kí hiệu là ![]() \(\dfrac{AB}{CD}\)
\(\dfrac{AB}{CD}\)
– Đoạn thẳng tỉ lệ: Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng A’B’ và C’D’ nếu có tỉ lệ thức:
![]() \(\frac{AB}{CD}=\frac{A'B'}{C'D'}\) hay
\(\frac{AB}{CD}=\frac{A'B'}{C'D'}\) hay ![]() \(\frac{AB}{A'B'}=\frac{CD}{C'D'}\)
\(\frac{AB}{A'B'}=\frac{CD}{C'D'}\)
B. Định lý Thales trong tam giác
1. Định lý Thales thuận trong tam giác
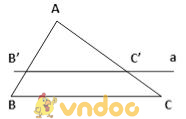
– Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
![]() \(B'C'//BC\Rightarrow\frac{AB'}{AB}=\frac{AC'}{AC};\frac{BB'}{AB}=\frac{CC'}{AC};\frac{AB'}{BB'}=\frac{AC'}{CC'}\)
\(B'C'//BC\Rightarrow\frac{AB'}{AB}=\frac{AC'}{AC};\frac{BB'}{AB}=\frac{CC'}{AC};\frac{AB'}{BB'}=\frac{AC'}{CC'}\)
2. Định lý Thales đảo
– Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Cho tam giác ABC nếu: ![]() \(\frac{AB'}{AB}=\frac{AC'}{AC}\)
\(\frac{AB'}{AB}=\frac{AC'}{AC}\)
![]() \(\frac{AB'}{BB'}=\frac{AC'}{CC'}\)
\(\frac{AB'}{BB'}=\frac{AC'}{CC'}\)
![]() \(\frac{BB'}{AB}=\frac{CC'}{AC}\)
\(\frac{BB'}{AB}=\frac{CC'}{AC}\)
![]() \(\Rightarrow B'C'//BC\)
\(\Rightarrow B'C'//BC\)
3. Hệ quả của định lí Thales
– Nếu một đường thẳng cắt hai cạnh (hoặc cắt phần kéo dài của hai cạnh) của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
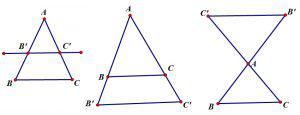
![]() \(\Rightarrow \frac{AB'}{AB}=\frac{AC'}{AC}=\frac{B'C'}{BC}\)
\(\Rightarrow \frac{AB'}{AB}=\frac{AC'}{AC}=\frac{B'C'}{BC}\)
C. Bài tập tự luyện
1. Câu hỏi trắc nghiệm
Bài 1. Viết tỉ số của các cặp đoạn thẳng có độ dài như sau:
a) AB = 6 cm; CD = 10 cm.
b) AB = 2 dm; MN = 4 cm.
c) MN = 12 cm; PQ = 2 dm
Bài 2: Tìm giá trị của x trên hình vẽ.
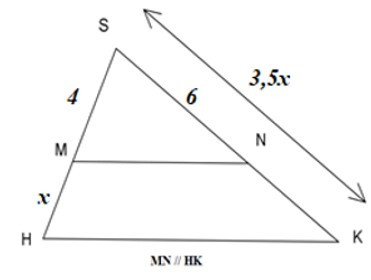
| A. x = 3 | B. x = 2,5 | B. x = 1 | D. x = 3,5 |
Bài 3: Cho hình vẽ, trong đó DE // BC, AE = 12, DB = 18, CA = 36. Độ dài AB bằng:
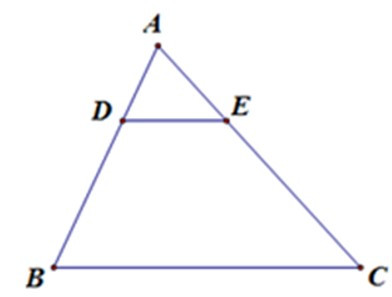
| A. 30 | B. 36 | C. 25 | D. 27 |
2. Câu hỏi tự luận
Bài tập 1: Cho tam giác ABC vuông tại A, đường cao AH. Gọi D là điểm đối xứng với A qua điểm B trên tia đối của tia HA lấy điểm E sao cho HE = 2HA. Gọi I là hình chiếu của D trên HE. Tính AB, AC, HC biết AH = 4 cm, HB = 3 cm
Bài tập 2: Cho hình bình hành ABCD. Gọi E, F, G lần lượt là trung điểm của AB, BC, CD. Dùng định lý Thales để chứng minh 2 đoạn thẳng DE và BG chia AC thành 3 đoạn bằng nhau
Bài tập 3: Cho hình thang ABCD có đáy nhỏ CD, từ D kẻ DK // BC (K thuộc AB), DK cắt AC tại M. Vẽ CF // AD (F thuộc AB). Qua F kẻ FP // AC (P thuộc BC). Chứng minh MP // AB
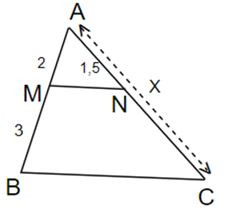
Bài tập 4: Cho tam giac ABC có M là trung điểm của AB, Từ M kẻ đường thẳng song song với BC cắt AC tại N. Chứng minh rằng N là trung điểm của AC
Bài tập 5: Áp dụng định lý Thales. Cho tam giác ABC, các trung tuyến AD, BE, CF cắt nhau tại G. Tính tỉ số AE/AC
Bài tập 6: Trên cạnh BC của hình vuông ABCD, lấy một đoạn BE = 1/3BC. Trên tia đối của tia CD, lấy một điểm F sao cho CF = 1/2BC, M là giao điểm của AE và BF. Chứng minh AM vuông góc với CM.
Bài 7: Hình thang ABCD (AB // CD, AB < CD) có hai đường chéo AC và BD cắt nhau tại O. Chứng minh rằng: OA.OD = OB.OC
Bài 8: Cho hình thang ABCD (AB // CD, AB < CD). Đường thẳng song song với đáy AB cắt các cạnh bên và đường chéo AD, BD, AC và BC theo thứ tự tại các điểm M, N, P, Q. Chứng minh rằng: MN = PQ.
Bài 9: Cho hình thang ABCD (AB // CD, AB < CD). Gọi trung điểm của các đường chéo AC và BD theo thứ tự là N và M. Chứng minh rằng:
a) MN // AB
b) MN = CD – AB/2
Bài 10: Hình thang ABCD (AB // CD, AB < CD) có 2 đường chéo AC và BD cắt nhau tại O. Đường thẳng qua O và song song với đáy AB cắt các cạnh bên AD và BC theo thứ tự tại M, N. Chứng minh rằng OM = ON.
Bài 11: Cho hình thang ABCD (AB // CD, AB < CD). Gọi M là trung điểm của CD. Gọi I là giao điểm của AM và BD, K là giao điểm của BM và AC.
a) Chứng minh: IK // AB.
b) Đường thẳng IK cắt AD, BC theo thứ tự ở E và F. Chứng minh: EI = IK = KF.
Bài 12: Cho hình thang ABCD có BC // AD. Trên AC kéo dài lấy 1 điểm P tùy ý. Đường thẳng qua P và trung điểm của BC cắt AB tại M và đường thẳng qua P và trung điểm của AD cắt CD tại N. Chứng minh rằng MN // AD.
Bài 13: Tứ giác ABCD có M, N lần lượt là trung điểm của các đường chéo AC và BD. Gọi G là trọng tâm tam giác ABC. Nối GC cắt MN tại O. Chứng minh rằng: OC = 3OG.
Bài 14. Tìm độ dài x cho hình vẽ sau biết MN // BC
Bài 15. Cho các đoạn thẳng AB = 4 cm; CD = 8 cm; MN = 20 cm; PQ = x cm. Tìm x để AB và CD tỉ lệ với MN và PQ?
Bài 16: Cho hình thang ABCD (AB // CD). Gọi trung điểm của các đường chéo AC và BD lần lượt là M, N. Chứng minh rằng MN, AB và CD song song với nhau.
Bài 17: Cho hình thang ABCD (AB // CD). Đường thẳng song song với đáy AB cắt các cạnh bên AD, BC và các đường chéo BD, AC lần lượt tại M, N, P, Q. Chứng minh ![]() \(\frac{MD}{AD}=\frac{CQ}{BC}\).
\(\frac{MD}{AD}=\frac{CQ}{BC}\).
Bài 18: Cho tam giác ABC vuông tại A, MN // BC (M thuộc AB, N thuộc AC), AB = 24 cm, AM = 16 cm, AN = 12 cm. Tính độ dài của các đoạn thẳng NC và NB.
Bài 19: Cho hình thang ABCD (AB < CD). Gọi trung điểm của các đường chéo AC và BD lần lượt là M, N. Chứng minh rằng MN, AB và CD song song với nhau.
Bài 20: Cho tam giác ABC có BC = 15 cm. Trên đường cao AH lấy các điểm I, K sao cho AK = KI = IH. Qua I, K vẽ các đường thẳng MN // BC, EF // BC.
a) Tính độ dài các đoạn thẳng EF và MN
b) Tính diện tích tứ giác MNEF, biết rằng diện tích của tam giác ABC là 270 cm2.
Tải về Chọn file muốn tải về:Bài tập Định lý Thales trong tam giác lớp 8
176,3 KB- Chia sẻ bởi:
 Công Tử
Công Tử

Có thể bạn quan tâm
Xác thực tài khoản!Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
Số điện thoại chưa đúng định dạng! Xác thực ngay Số điện thoại này đã được xác thực! Bạn có thể dùng Sđt này đăng nhập tại đây! Lỗi gửi SMS, liên hệ Admin Sắp xếp theo Mặc định Mới nhất Cũ nhất-
Đại số
- Chương 1: Phép nhân và phép chia các đa thức
- Bài tập Toán 8: Nhân đơn thức với đa thức
- Bài tập Toán 8: Nhân đa thức với đa thức
- Bài tập Toán 8: Những hằng đẳng thức đáng nhớ
- Bài tập Toán 8: Những hằng đẳng thức đáng nhớ (tiếp)
- Bài tập Toán 8: Những hằng đẳng thức đáng nhớ (tiếp theo)
- Bài tập nâng cao Toán 8: Những hằng đẳng thức đáng nhớ
- Bài tập nâng cao Toán 8: Những hằng đẳng thức đáng nhớ (Tiếp theo)
- Công thức Những hằng đẳng thức đáng nhớ
- 7 Hằng Đẳng Thức Đáng Nhớ Và Hệ Quả
- Bài tập Toán 8: Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
- Bài tập Toán 8: Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
- Bài tập Toán 8: Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
- Bài tập Toán 8: Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp
- Bài tập nâng cao Toán 8: Phân tích đa thức thành nhân tử
- Bài tập Toán 8: Chia đơn thức cho đơn thức
- Bài tập Toán 8: Chia đa thức cho đơn thức
- Bài tập Toán 8: Chia đa thức một biến đã sắp xếp
- Bài tập nâng cao Toán 8: Phép chia các đa thức
- Bài tập Ôn tập chương 1 Đại số Toán 8
- Chương 2: Phân thức đại số
- Bài tập Phân thức đại số Toán 8
- Chương 3: Phương trình bậc nhất một ẩn
- Bài tập Toán lớp 8: Mở đầu về phương trình
- Bài tập Toán lớp 8: Phương trình bậc nhất một ẩn và cách giải
- Bài tập Toán lớp 8: Phương trình đưa được về dạng ax+b=0
- Bài tập Toán lớp 8: Phương trình tích
- Bài tập Toán lớp 8: Phương trình chứa ẩn ở mẫu
- Bài tập Toán lớp 8: Giải bài toán bằng cách lập phương trình
- Phương trình bậc nhất và đồ thi hàm số bậc nhất
- Bài tập Hàm số bậc nhất y = ax + b, a ≠ 0
- Bài tập Đồ thị của hàm số bậc nhất y = ax + b, a ≠ 0
- Chương 4: Bất phương trình bậc nhất một ẩn
- Chương 1: Phép nhân và phép chia các đa thức
-
Hình học
- Chương 1: Tứ giác
- Bài tập Toán 8: Tứ giác
- Bài tập nâng cao Toán 8: Tứ giác
- Bài tập Toán 8: Hình thang
- Bài tập Đường thẳng song song với một đường thẳng cho trước Toán 8
- Bài tập Hình thoi Toán 8
- Chương 2: Đa giác - Diện tích đa giác
- Chương 3: Tam giác đồng dạng
- Chương 4: Hình lăng trụ đứng - Hình chóp đều
- Chương 1: Tứ giác
-
 Lớp 8
Lớp 8 -
 Toán 8
Toán 8 -
 Bài tập Toán 8
Bài tập Toán 8 -
 Đề thi giữa kì 1 lớp 8
Đề thi giữa kì 1 lớp 8 -
 Đề thi học kì 1 lớp 8
Đề thi học kì 1 lớp 8 -
 Đề thi giữa kì 2 lớp 8
Đề thi giữa kì 2 lớp 8 -
 Đề thi học kì 2 lớp 8
Đề thi học kì 2 lớp 8 -
 Đề kiểm tra 15 phút lớp 8
Đề kiểm tra 15 phút lớp 8 -
 Thi học sinh giỏi lớp 8
Thi học sinh giỏi lớp 8 -
 Toán 8 Kết nối tri thức
Toán 8 Kết nối tri thức -
 Toán 8 Chân trời sáng tạo
Toán 8 Chân trời sáng tạo -
 Toán 8 Cánh diều
Toán 8 Cánh diều -
 Giải Bài Tập Toán 8
Giải Bài Tập Toán 8 -
 Lý thuyết Toán 8
Lý thuyết Toán 8 -
 Soạn Toán 8 VNEN
Soạn Toán 8 VNEN
Tham khảo thêm
-
Giải bài tập SGK Toán lớp 8 bài 7: Hình chóp đều và hình chóp cụt đều
-
Bài tập Hình chóp đều tam giác, hình chóp đều tứ giác lớp 8
-
Bài tập Phân thức đại số Toán 8
-
Giải bài tập SGK Toán lớp 8 bài 2: Hình hộp chữ nhật (tiếp)
-
Giải bài tập SGK Toán lớp 8 bài 6: Thể tích của hình lăng trụ đứng
-
Giải bài tập SGK Toán lớp 8 bài 5: Diện tích xung quanh của hình lăng trụ đứng
-
Giải bài tập SGK Toán lớp 8 bài 3: Thể tích của hình hộp chữ nhật
-
Bài tập Đường trung bình của tam giác lớp 8
-
Giải bài tập SGK Toán lớp 8 bài 4: Hình lăng trụ đứng
-
Bài tập Tính chất đường phân giác của tam giác lớp 8

Bài tập Toán 8
-
Bài tập Định lý Thales trong tam giác lớp 8
-
Bài tập Hình chóp đều tam giác, hình chóp đều tứ giác lớp 8
-
Bài tập Tính chất đường phân giác của tam giác lớp 8
-
Bài tập Đường trung bình của tam giác lớp 8
-
Bài tập Định lí Pythagore lớp 8
-
Bài tập Phân thức đại số Toán 8

Gợi ý cho bạn
-
Bài tập cuối tuần môn Toán lớp 6 Cánh diều - Tuần 1
-
Được 18-20 điểm khối A1 nên đăng ký trường nào?
-
TOP 13 Viết thư cho ông bà để hỏi thăm và kể về tình hình gia đình em lớp 4
-
Bài tập tiếng Anh lớp 10 Unit 1 Family life nâng cao
Bài tập Định lý Thales trong tam giác lớp 8
Bài tập Định lý Thales trong tam giác lớp 8
Chỉ mua tài liệu trên 15.000đ Ưu đãi kèm thêmMua gói VnDoc Pro chỉ với giá
79.000đ 59.000đ- 30 lượt tải tài liệu thường
- 10.000+ bài luyện Trắc nghiệm trực tuyến
- Không quảng cáo
Thông tin thanh toán nhanh
Tên tài liệu:Bài tập Định lý Thales trong tam giác lớp 8
15.000đ
Số điện thoại/emailVui lòng nhập số điện thoại hoặc email hợp lệ.
Tải nhanh tài liệu này 15.000đ Hỗ trợ Zalo × ← Thanh toán 15.000đ để tải tài liệu- Tên tài khoản:CÔNG TY CỔ PHẦN MẠNG TRỰC TUYẾN META
- Số tài khoản:1038633514Copy
- Ngân hàng:Vietcombank
- Số tiền:15.000đ
- Nội dung bắt buộc*: Copy

Vui lòng giữ đúng nội dung KH khi chuyển khoản và giữ nguyên cửa sổ này để tải tài liệu tự động.
Hỗ trợ ZaloTừ khóa » định Lý Ta Lét Trong Hình Thang
-
Định Lý Talet Trong Tam Giác, Trong Hình Thang – Toán Lớp 8
-
Định Lý Talet Tam Giác, định Lý Talet Trong Hình Thang, Hệ Quả Và Bài ...
-
Định Lí Thales Trong Hình Thang, Hệ Quả Và Cách áp Dụng Cực Hay
-
Tìm Hiểu Về định Nghĩa Và Những Hệ Quả Của định Lý Talet - VOH
-
Định Lý Talet Trong Tam Giác, Trong Hình Thang – Toán ... - Wiki Hỏi Đáp
-
Top 15 Hệ Quả định Lí Ta Lét Trong Hình Thang
-
Định Lý Talet Thuận, định Lý Talet đảo Và Hệ Quả Của định Lý Talet
-
Định Lý Talet Và Những Hệ Quả Của định Lý Talet
-
Định Lí Ta Lét Trong Tam Giác Và Những Hệ Quả Bạn Cần Biết
-
Định Lý Talet Trong Tam Giác, Trong Hình Thang – Toán Lớp 8 - .vn
-
Định Lí Ta-lét. Định Lí đảo Và Hệ Quả Của định Lí Ta-lét
-
[Định Lý Talet (Thales)] Định Lý Talet Và Những Hệ Quả Của Chúng
-
Sử Dụng Hệ Quả Của định Lí Ta-lét để Tính độ Dài Của đoạn Thẳng
-
Định Lý Thales – Wikipedia Tiếng Việt
































