Toán Tử Bitwise - Viblo
Có thể bạn quan tâm
Toán tử bitwise trong c++
C++ cung cấp cho ta 6 thao tác toán tử , thường được gọi là toán tử bitwise.
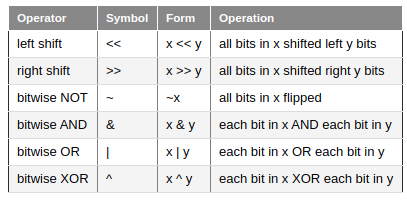
trong các ví dụ bên dưới đây, phần lớn chúng ta làm việc với hệ nhị phân 4 bit. điều này thuận tiện cho việc đơn giản hóa ví dụ.
Toán tử dịch bit trái (<<) và toán tử dịch bit phải (>>). Trong phép dịch trái thì toán hạng bên trái là biểu thức để dịch chuyển các bit, còn toán hạng bên phải là con số bit cần dịch chuyển. vì vậy, khi chúng ta viết x<<1, nghĩa là chúng ta dịch chuyển x sang trái 1 bit. các bit mới được dịch chuyển bên phải sẽ là 0.
0011 << 1 == 0110 0011 << 2 == 1100 0011 << 3 == 1000Lưu ý rằng trong trường hợp thứ ba, chúng tôi đã thay đổi một chút về cuối số! Các bit được dịch chuyển ra khỏi cuối số nhị phân sẽ bị mất vĩnh viễn. Tương tự với trường hợp dịch bit phải.
1100 >> 1 == 0110 1100 >> 2 == 0011 1100 >> 3 == 0001ở trường hợp thứ 3 cũng giống như trên, bít cuối bị mất và và các bit bên trái được chèn 0 vào. Dưới đây là một ví dụ về dịch chuyển bit:
#include <bitset> #include <iostream> int main() { std::bitset<4> x { 0b1100 }; std::cout << x << '\n'; std::cout << (x >> 1) << '\n'; std::cout << (x << 1) << '\n'; return 0; }kết quar:
1100 0110 1000Bitwise NOT
Toán tử bitwise NOT (~) có lẽ là dễ hiểu nhất trong tất cả các toán tử bitwise. Nó chỉ đơn giản là lật từng bit từ 0 thành bit 1 hoặc ngược lại. Lưu ý rằng kết quả của NOT phụ thuộc vào kích thước loại dữ liệu của bạn. lật 4 bits: ~0100 là 1011
lật 8 bits: ~0000 0100 là 1111 1011
Trong cả hai trường hợp 4 bit và 8 bit, chúng ta bắt đầu với cùng một số (nhị phân 0100 giống với 0000 0100 theo cùng cách mà số thập phân 7 giống với 07), nhưng chúng tôi kết quả với một kết quả khác. Chúng ta có thể thấy điều này trong ví dụ dưới đây:
#include <bitset> #include <iostream> int main() { std::cout << std::bitset<4>{ ~0b0100u } << ' ' << std::bitset<8>{ ~0b0100u }; return 0; }kết quả cho ra là: 1011 11111011
Bitwise OR
Bitwise OR (|) hoạt động giống như cái tên của nó (là hoặc). Tuy nhiên, thay vì áp dụng OR cho các toán hạng để tạo ra một kết quả duy nhất, bitwise OR áp dụng cho từng bit! Ví dụ, hãy xem xét biểu thức 0b0101 | 0b0110.
Để thực hiện (bất kỳ) thao tác bitwise, cách dễ nhất là sắp xếp hai toán hạng lên như thế này:
0 1 0 1 OR 0 1 1 0sau đó áp dụng việc tính toán cho từng cột bit. Trong 1 cột có ít nhất 1 số 1 thì cho kết quả là 1, còn lại là 0:
0 1 0 1 OR 0 1 1 0 ----------- 0 1 1 1Ta viết bằng code c++ như sau:
#include <bitset> #include <iostream> int main() { std::cout << (std::bitset<4>{ 0b0101 } | std::bitset<4>{ 0b0110 }); return 0; }kết quả : 0111
Chúng ta có thể làm điều tương tự với các biểu thức OR, chẳng hạn như 0b0111 | 0b0011 | 0b0001 như sau:
0 1 1 1 OR 0 0 1 1 OR 0 0 0 1 -------- 0 1 1 1viết bằng code c++:
#include <bitset> #include <iostream> int main() { std::cout << (std::bitset<4>{ 0b0111 } | std::bitset<4>{ 0b0011 } | std::bitset<4>{ 0b0001 }); return 0; }kết quả : 0111.
Bitwise AND
Bitwise AND (&) hoạt động tương tự như trên. Logic AND được đánh giá là đúng nếu cả toán hạng trái và phải đánh giá là đúng. Bitwise AND cho kết quả là đúng (1) nếu cả hai bit trong cùng một cột là 1. Hãy xem xét biểu thức 0b0101 & 0b0110. Sắp xếp từng bit lên và áp dụng thao tác AND cho từng cột bit:
0 1 0 1 AND 0 1 1 0 -------- 0 1 0 0ví dụ :
#include <bitset> #include <iostream> int main() { std::cout << (std::bitset<4>{ 0b0101 } & std::bitset<4>{ 0b0110 }); return 0; }kết quả cho ra:
0100
Tương tự, chúng ta có thể làm điều tương tự với các biểu thức AND, chẳng hạn như 0b0001 & 0b0011 & 0b0111. Nếu tất cả các bit trong một cột là 1, kết quả của cột đó là 1.
0 0 0 1 AND 0 0 1 1 AND 0 1 1 1 -------- 0 0 0 1ví dụ :
#include <bitset> #include <iostream> int main() { std::cout << (std::bitset<4>{ 0b0001 } & std::bitset<4>{ 0b0011 } & std::bitset<4>{ 0b0111 }); return 0; }kết quả :
0001Bitwise XOR
Toán tử cuối cùng là XOR bitwise (^). Khi đánh giá hai toán hạng, XOR cho kết quả là đúng (1) nếu một và chỉ một trong các toán hạng của nó là đúng (1). Nếu cả 2 đều đúng hoặc không đúng thì nó cho kết quả là 0. Hãy xem xét biểu thức 0b0110 ^ 0b0011:
0 1 1 0 XOR 0 0 1 1 ------- 0 1 0 1Ta cũng có thể đánh giá kiểu cột biểu thức XOR ghép, chẳng hạn như 0b0001 ^ 0b0011 ^ 0b0111. Nếu có số chẵn bit 1 trong một cột, kết quả là 0. Nếu có một số lẻ bit 1 trong một cột, kết quả là 1.
0 0 0 1 XOR 0 0 1 1 XOR 0 1 1 1 -------- 0 1 0 1Phép gán toán tử bitwise
Tương tự như các toán tử gán số học, C ++ cung cấp các toán tử gán bit theo thứ tự để tạo điều kiện dễ dàng sửa đổi các biến.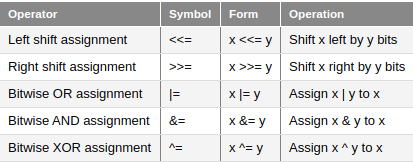
ví dụ : ta có phép gán là x = x >> 1 cách viết này tương đương với x >>= 1.
#include <bitset> #include <iostream> int main() { std::bitset<4> bits { 0b0100 }; bits >>= 1; std::cout << bits; return 0; }chương trình này cho kết quả :
0010Từ khóa » Toán Tử Dịch Phải Bit
-
Phép Toán Thao Tác Bit – Wikipedia Tiếng Việt
-
BIT MATH – Các Phép Toán Thao Tác Trên Bit
-
Các Thao Tác Trên Bit — Modern C++ - STDIO
-
Phép Toán Thao Tác Bit Trong C++ (Bitwise Operation)
-
Chương 11: Phép Thao Tác Trên Các Số Nhị Phân
-
Hỏi Về Phép Dịch Phải Dịch Trái Trong C/c++ - Programming
-
Phép Toán Thao Tác Bit - Wiki Là Gì
-
C - Bài 08B: Toán Tử Thao Tác Trên Bit - YouTube
-
Toán Tử Dịch Bit - 123doc
-
Các Toán Tử Thao Tác Trên Bit - TEK4
-
Phép Toán Thao Tác Bit - VOER - Thư Viện Học Liệu Mở Việt Nam
-
Toán Tử Logic, Toán Tử Trên Bit Và Toán Tử Gán Trong C++ - Góc Học IT
-
Dịch Chuyển Và Quay Bit Phép_toán_thao_tác_bit - Tieng Wiki
-
Toán Tử Thao Tác Bit Trong Java
-
Toán Tử Thao Tác Bit Trong Python
-
Các Toán Tử Bitwise - Openplanning
-
Tự Học C/C++ | Toán Tử Bitwise »
-
Fun With Bits - VNOI
-
Hiểu Nhanh Toán Tử Thao Tác Bit Trong Java - Techmaster