Tốc độ Trung Bình Trong Khoảng Thời Gian - .vn

Để xác định được tốc độ trung bình trong khoảng thời gian cho trước thì học sinh cần phải xác định được quãng đường đi được trong khoảng thời gian đó. Như vậy, bài tìm tốc độ trung bình hay vận tốc trung bình là dạng bài tổng quát của dao động điều hòa. Để hiểu rõ và chi tiết hơn, chúng ta cùng nhau tìm hiểu.

Xét một chất điểm dao động điều hòa có phương trình x = Acos(ωt + φ). Gọi:

• ${x_1},\,{x_2}$ lần lượt là li độ ở thời điểm t$_1$ và t$_2$
• S là quãng đường vật đi từ thời điểm t$_1$ đến thời điểm t$_2$

Khi đó:

• Vận tốc trung bình của vật trong khoảng thời gian ∆t: ${v_{tb}} = \frac{{\left| {{x_2} – {x_1}} \right|}}{{\Delta t}}$
• Tốc độ trung bình của vật trong khoảng thời gian ∆t: $\,\overline {{v_{tb}}} = \frac{S}{{\Delta t}} = \frac{S}{{{t_2} – {t_1}}}$

Yêu cầu: Để giải tốc được bài tốc độ trung bình, học sinh làm được các bài dao động cơ như tìm quãng đường, tìm thời điểm dao động trước và sau thời điểm đã cho.

Câu 1: Một vật dao động điều hòa với biên độ A = 8 cm và chu kì T = 0,4 s. Tốc độ trung bình lớn nhất của vật trong khoảng thời gian Δt = 1/15 s là A. 1,5 m/s. B. 1,8 m/s. C. 1,2 m/s. D. 2,1 m/s. Giải $\Delta t = \frac{1}{{15}}\left( s \right) < \frac{T}{2} = 0,2\left( s \right) \to {S_{\max }} = 2A\sin \frac{{\omega .\Delta t}}{2} = 8\left( {cm} \right) \to {v_{tb\max }} = \frac{{{s_{\max }}}}{{\Delta t}} = 1,2\left( {\frac{m}{s}} \right)$

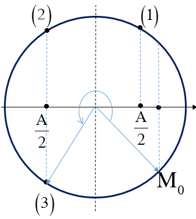
Câu 2: Một chất điểm dao động điều hòa với chu kì T. Tốc độ trung bình lớn nhất của chất điểm trong thời gian T/6 là v. Tốc độ cực đại của vật bằng A. $\frac{{2\pi v}}{3}.$ B. $\frac{{\pi v}}{2}.$ C. $\frac{{3\pi v}}{4}.$ D. $\frac{{\pi v}}{3}.$

giải $\left\{ \begin{array}{l} t = \frac{T}{6}\\ {s_{\max }} = A \end{array} \right. \to v = \frac{{{s_{\max }}}}{t} \leftrightarrow v = \frac{{6A}}{T} = 3\frac{{\omega A}}{\pi } \to {v_{\max }} = \omega A = \frac{{\pi v}}{3}$

Câu 3: Một vật dao động điều hòa với phương trình vận tốc v = 10πcos(πt + π/3) cm/s. Tốc độ trung bình của vật trên quãng đường từ thời điểm ban đầu tới thời điểm li độ có độ lớn bằng nửa biên độ lần thứ 3 là A. 13,33 cm/s. B. 17,56 cm/s. C. 15 cm/s. D. 20 cm/s. Giải $\begin{array}{l} v = 10\pi \cos \left( {\pi t + \frac{\pi }{3}} \right) \to \left\{ \begin{array}{l} A = \frac{{{v_{\max }}}}{\omega } = 10\left( {cm} \right)\\ {\varphi _x} = \frac{\pi }{3} – \frac{\pi }{2} = – \frac{\pi }{6} \end{array} \right. \to x = 10\cos \left( {\pi t – \frac{\pi }{6}} \right)\left( {cm} \right)\\ \left. \begin{array}{l} \left\{ \begin{array}{l} t = 0\\ x = 5\sqrt 3 cm\\ v > 0 \end{array} \right.\\ \left| x \right| = \frac{A}{2} = 5\left( {cm} \right) \end{array} \right\} \to \left\{ \begin{array}{l} t = \frac{\varphi }{\omega } = \frac{{2\pi – \left( {\frac{\pi }{6} + \frac{\pi }{3}} \right)}}{\pi } = \frac{3}{2}\left( s \right)\\ s = 4A – \frac{A}{2} – \frac{{A\sqrt 3 }}{2} = 4\left( {cm} \right) \end{array} \right. \to \overline {{v_{tb}}} = \frac{s}{t} = 17,56\left( {\frac{{cm}}{s}} \right) \end{array}$

Câu 4: Một vật dao động điều hòa với phương trình x = 6cos(20πt – π/12), x tính bằng cm và t tính bằng s. Vận tốc trung bình của vật đi từ vị trí cân bằng đến vị trí có li độ x = + 3cm lần đầu tiên là: A. 0,36 m/s B. 3,6 m/s C. 36 cm/s D. 6,3 m/s Giải $\begin{array}{l} \left. \begin{array}{l} {x_1} = 0\\ {x_2} = 3\left( {cm} \right)\\ {t_{x = 0 \to x = 2,5\left( {cm} \right) = \frac{A}{2}}} = \frac{T}{{12}} = \frac{{\frac{{2\pi }}{{20\pi }}}}{{12}} = \frac{1}{{120}}\left( s \right) \end{array} \right\}\\ \to {v_{tb}} = \frac{{\left| {{x_2} – {x_1}} \right|}}{t} = \frac{{3 – 0}}{{\frac{1}{{120}}}} = 360\left( {\frac{{cm}}{s}} \right) = 3,6\left( {\frac{m}{s}} \right) \end{array}$ Chọn: B.

Câu 5: Một vật dao động điều hòa theo phương trình x = 5cos(2πt – π/4), x tính bằng cm và t tính bằng s. Tốc độ trung bình của vật trong khoảng thời gian từ t$_1$ = 1s đến t$_2$ = 4,625s là: A. 15,5 cm/s B. 17,4 cm/s C. 2,4 cm/s D. 19,7 cm/s Giải $\begin{array}{l} {t_1} = 1\left( s \right) \to \left\{ \begin{array}{l} {x_1} = 5\cos \left( {2\pi .1 – \frac{\pi }{4}} \right) = \frac{{5\sqrt 2 }}{2}\left( {cm} \right)\\ {v_1} = – 5.2\pi \sin \left( {2\pi .1 – \frac{\pi }{4}} \right) > 0 \end{array} \right.\\ {t_2} = 4,625\left( s \right) \to \left\{ \begin{array}{l} {x_2} = 5\cos \left( {2\pi .4,625 – \frac{\pi }{4}} \right) = – 5\left( {cm} \right)\\ {v_2} = – 5.2\pi \sin \left( {2\pi .4,625 – \frac{\pi }{4}} \right) = 0 \end{array} \right. \end{array}$ $T = \frac{{2\pi }}{\omega } = 1\left( s \right) \to \Delta t = {t_2} – {t_1} = 3,625\left( s \right) = 3T + \frac{{5T}}{8}$ $\left. \begin{array}{l} {v_1}.{v_2} = 0\\ \Delta t’ = \frac{{5T}}{8} > \frac{T}{2} \end{array} \right\} \to {S_2} = 4A – \left| {{x_2} – {x_1}} \right| = 4.5 – \left| {\frac{{5\sqrt 2 }}{2} – \left( { – 5} \right)} \right| = 11,46\left( {cm} \right)$ Quãng đường vật đi được: S = S1 + S2 = 60 + 15 = 71,45 cm Tốc độ trung bình: $\overline {{v_{tb}}} = \frac{S}{{\Delta t}} = \frac{{71,46}}{{3,625}} = 19,71\left( {\frac{{cm}}{s}} \right)$ Chọn: D.