Tổng Hợp Kiến Thức Hình Học Lớp 9 - Tài Liệu Môn Toán ...

Trang chủ » Các Dạng Toán Hình Lớp 9 Học Kì 1 » Tổng Hợp Kiến Thức Hình Học Lớp 9 - Tài Liệu Môn Toán ...

Có thể bạn quan tâm

Hệ thống các kiến thức Hình học lớp 9

Hình học lớp 9 là một trong những nội dung quan trọng nhất trong chương trình Toán THCS, đồng thời cũng là phần kiến thức nền tảng phục vụ trực tiếp cho kỳ thi tuyển sinh vào lớp 10. Việc nắm chắc các định lý, hệ thức và phương pháp giải trong hình học không chỉ giúp học sinh rèn luyện kỹ năng tư duy logic, mà còn nâng cao khả năng giải quyết các bài toán thực tế. Bài viết này sẽ tổng hợp kiến thức Hình học lớp 9 một cách đầy đủ, khoa học và dễ hiểu, đồng thời gợi ý các bài tập minh họa có đáp án chi tiết để học sinh thuận tiện trong việc ôn tập. Đây chắc chắn sẽ là tài liệu môn Toán lớp 9 hữu ích, hỗ trợ học sinh học tập và luyện thi hiệu quả.

Chương I. Hệ thức lượng trong tam giác

1. Hệ thức về cạnh và đường cao trong tam giác vuông

Cho tam giác ABC vuông tại A, đường cao AH:

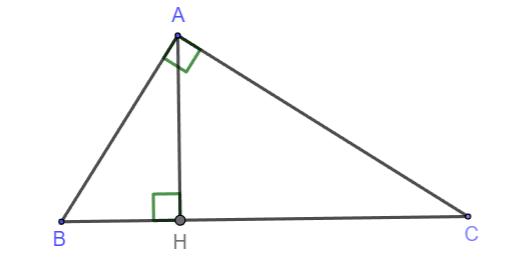
Định lý Pythagore: BC^{2} = AB^{2} + AC^{2}

Phát biểu thành lời: Trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông của tam giác đó.

AB^{2} = BC.BH              AC^{2} = BC.CH

AH^{2} = BH.CH                  AB.AC = BC.AH                \frac{1}{AH^{2}} = \frac{1}{AB^{2}} + \frac{1}{AC^{2}}

2. Tỉ số lượng giác của góc nhọn

Hình vẽ minh họa:

\sin\alpha = \frac{AC}{BC};cos\alpha = \frac{AB}{BC}

Sin α bằng cạnh đối chia cạnh huyền

cos α bằng cạnh kề trên cạnh huyền

\tan\alpha = \frac{AC}{AB};cot\alpha = \frac{AB}{AC}

Tan α bằng cạnh đối trên cạnh kề

Cot α bằng cạnh kề trên cạnh đối

Nếu hai góc phụ nhau thì sin góc này bằng cosin góc kia, tang góc này bằng cotang góc kia.

Nếu \alpha + \beta = 90^{0} thì

\sin\alpha = \cos\beta                   \cos\alpha = \sin\beta

\tan\alpha = \cot\beta                \cot\alpha = \tan\beta

Với hai góc nhọn \alpha;\beta. Nếu ta có: \sin\alpha = \sin\beta (hoặc \cos\alpha = \cos\beta; \tan\alpha = \tan\beta; \cot\alpha = \cot\beta) thì ta có \alpha = \beta.

Bảng tỉ số lượng giác của một số góc đặc biệt:

3. Giải tam giác

Hình vẽ minh họa

Cho a, b, c là độ dài ba cạnh của tam giác ABC vuông tại A:

b = a.sin\widehat{B} = a.cos\widehat{C}                   c = a.sin\widehat{C} = a.cos\widehat{B}

b = c.tan\widehat{B} = c.cot\widehat{C}                    c = b.tan\widehat{C} = b.cot\widehat{B}

Tam giác ABC vuông tại A suy ra BC = \sqrt{AB^{2} + AC^{2}}

AB = \sqrt{BC^{2} - AC^{2}};AC = \sqrt{BC^{2} - AB^{2}}

Tam giác ABC vuông tại A có \widehat{C} = 30^{0} \Rightarrow AB = \frac{BC}{2}

Tam giác ABC vuông tại A có \widehat{B} = 60^{0} \Rightarrow AC = \frac{BC\sqrt{3}}{2}

Công thức tính diện tích tam giác

S_{\Delta ABC} = \frac{1}{2}ab.sin\widehat{C} = \frac{1}{2}bc.sin\widehat{A} = \frac{1}{2}ac.sin\widehat{B}

Phát biểu thành lời: Diện tích tam giác bằng một nửa tích hai cạnh kề với sin góc xen giữ hai cạnh đó.

S_{\Delta ABC} = p.r = \frac{abc}{4R}

R là bán kính đường tròn ngoại tiếp tam giác ABC

R là bán kính đường tròn nội tiếp tam giác ABC.

Trong tam giác bất kì ta có: \frac{b}{\sin\widehat{B}} = \frac{a}{\sin\widehat{A}} = \frac{c}{\sin\widehat{C}}

Chương II. Đường tròn

1. Định nghĩa và sự xác định của đường tròn

a. Định nghĩa: Tập hợp các điểm cách O một khoảng cố định không đổi bằng R là đường tròn tâm O, bán kính R. Kí hiệu: Đường tròn (O: R) hay đường tròn (O)

b. Vị trí của một điểm đối với đường tròn

Điểm M nằm trên đường tròn (O; R) ⇔ OM = R

Điểm M nằm bên ngoài đường tròn (O; R) ⇔ OM > R

Điểm M nằm bên trong đường tròn (O; R) ⇔ OM < R

c. So sánh độ dài dây và đường kính

Định lý: Đường kính là dây cung lớn nhất của đường tròn:

d. Sự xác định của đường tròn

Định lý: Đường tròn đi qua ba đỉnh A; B; C của tam giác ABC gọi là đường tròn ngoại tiếp tam giác ABC. Tam giác ABC gọi là tam giác nội tiếp đường tròn

Tâm của đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của các cạnh tam giác.

2. Tính chất đối xứng của đường tròn

a. Liên hệ giữa đường kính và dây cung

Định lý: Đường kính vuông góc với một dây thì đi qua trung điểm của dây đó:

(Đường tròn (O) có OM⊥AB tại I => I là trung điểm của AB)

Định lý đảo: Đường kính đi qua trung điểm của một dây (dây không là đường kính) thì vuông góc với dây đó. (Đường tròn (O) có OM cắt AB tại I và I là trung điểm của dây AB => OM⊥AB tại I).

b. Liên hệ giữa dây và khoảng cách đến tâm

Định lý: Trong một đường tròn:

  • Hai dây bằng nhau thì cách đều tâm:

(Đường tròn (O) có AB = CD; OI⊥AB tai I, OK⊥CD tại K => OI⊥OK)

  • Hai dây cách đều tâm thì bằng nhau

(Đường tròn (O) có OI⊥AB tại I, OK⊥CD tại K; OI = OK => AB = CD)

Tài liệu quá dài để hiển thị hết — hãy nhấn Tải về để xem trọn bộ!

-------------------------------------------------------------------------

Có thể nói, tổng hợp kiến thức Hình học lớp 9 chính là kim chỉ nam giúp học sinh hệ thống lại toàn bộ chuyên đề trọng tâm như hệ thức lượng trong tam giác vuông, đường tròn, tứ giác nội tiếp, các bài toán thực tế,… Việc học theo hệ thống không chỉ giúp tiết kiệm thời gian ôn tập, mà còn giúp các em dễ dàng nhận diện dạng bài, chọn phương pháp giải phù hợp và hạn chế sai sót. Với tài liệu này, học sinh hoàn toàn có thể tự học ở nhà, củng cố lại phần kiến thức đã học trên lớp và nâng cao khả năng giải toán. Đây cũng là hành trang vững chắc để bước vào kỳ thi tuyển sinh lớp 10 môn Toán với sự tự tin và kết quả cao nhất.

Từ khóa » Các Dạng Toán Hình Lớp 9 Học Kì 1