Tổng Hợp Lý Thuyết Và Bài Tập Chuyên đề Giới Hạn

Download.vn Hướng dẫn sử dụng, mẹo vặt, thủ thuật phần mềm tài liệu và học tập Thông báo Mới

• Tất cả
  • Học tập
  • Tài liệu
  • Hướng dẫn
• • Học tập
  • Tài liệu
  • Hướng dẫn
  • Đề thi
  • Học tiếng Anh
  • Giáo án
  • Bài giảng điện tử
  • Tài liệu Giáo viên
  • Tập huấn Giáo viên

Gói Thành viên của bạn sắp hết hạn. Vui lòng gia hạn ngay để việc sử dụng không bị gián đoạn Download.vn Học tập Lớp 11 Toán 11 Lý thuyết và bài tập chuyên đề giới hạn Tổng hợp lý thuyết và bài tập chuyên đề giới hạn Tải về Bình luận

• 5

Mua gói Pro để tải file trên Download.vn và trải nghiệm website không quảng cáo

Tìm hiểu thêm » Mua Pro 79.000đ Hỗ trợ qua Zalo

Lý thuyết và bài tập chuyên đề giới hạn là tài liệu vô cùng hữu ích mà Download.vn muốn giới thiệu đến quý thầy cô cùng các bạn học sinh lớp 11 cùng tham khảo.

Tài liệu gồm 75 trang tóm tắt lý thuyết chuyên đề giới hạn và tuyển chọn bài tập tự luận, trắc nghiệm giới hạn dãy số, giới hạn hàm số và hàm số liên tục có đáp án và lời giải chi tiết giúp học sinh học tốt chương trình Đại số và Giải tích 11 chương 4. Sau đây là nội dung chi tiết, mời bạn đọc cùng tham khảo và tải tại đây.

Tổng hợp lý thuyết và bài tập chuyên đề giới hạn

MỤC LỤC PHẦN I. LÝ THUYẾT VÀ BÀI TẬP TỰ LUẬN §1. GIỚI HẠN CỦA DÃY SỐ 01 - 14 §2. GIỚI HẠN CỦA HÀM SỐ 15 – 31 §3. HÀM SỐ LIÊN TỤC 32 – 40 ÔN TẬP CHƯƠNG IV 41 – 49 PHẦN II. TRẮC NGHIỆM GIỚI HẠN CỦA DÃY SỐ 50 – 54 GIỚI HẠN CỦA HÀM SỐ 55 – 59 HÀM SỐ LIÊN TỤC 60 – 62 ÔN TẬP CHƯƠNG IV. GIỚI HẠN 63 – 72 ĐÁP ÁN TRẮC NGHIỆM 73 – 74 Toán 11 GV. Lư Sĩ Pháp 1 BT. ĐS&GT 11 Chương IV. Giới hạn CHƯƠNG IV. GIỚI HẠN PHẦN I. LÝ THUYẾT VÀ BÀI TẬP TỰ LUẬN §1. GIỚI HẠN CỦA DÃY SỐ A. KIẾN THỨC CẤN NẮM 1. Giới hạn hữu hạn của dãy số nnulim0→+∞= khi và chỉ khi nu có thể nhỏ hơn một số dương bé tùy ý, kể từ một số hạng nào đó trở đi. nnnnvavalimlim()0→+∞→+∞=⇔−=  Dãy số (un) có giới hạn 0 khi và chỉ khi dãy số ()nucó giới hạn 02. Giới hạn vô cực nnulim→+∞= +∞ khi và chỉ khi nucó thể lớn hơn một số dương lớn tùy ý, kể từ một số hạng nào đó trở đi. Kí hiệu: nnu hay u khi nlim= +∞→+∞→+∞  Dãy số (nu) được gọi là có giới hạn −∞ khi n→+∞ nếu nulim()−= +∞  Nhận xét: nnnnuulimlim()→+∞→+∞= +∞⇔−= −∞; nnnnuulimlim()→+∞→+∞= −∞⇔−= +∞ Lưu ý: Thay cho viết nnnnuLulim, lim→+∞→+∞== ±∞, ta viết nnuaulim,lim== ±∞ 3. Các giới hạn đặc biệt a)n1lim0=; kn1lim0=; knlim= +∞, với k nguyên dương.b)nqlim0=, nếu q1<; nqlim= +∞ nếu q > 1c)cclim=; kcnlim0=, lim(c un) = climun, với c là hằng số,k*∈ℕ d)nnqlim0= nếu q1> 4. Định lí về giới hạn hữu hạn Định lí 1. Nếu nuLlim= và nvMlim=, thì:nnnnuvuvLMlim()limlim+=+=+ nnnnuvuvLMlim()limlim−=−=− nnnnuvuvLMlim.lim.lim.==ncuc Llim(.).= ( với c là hằng số) nnuLvMlim= (nếu M0≠) Định lí 2. Giả sửnuLlim=  Nếu nu0≥ với mọi n thì L0≥ và nuLlim= nuLlim= và nuL33lim=  Nếu nulim= +∞ thì nu1lim0= 5.Một vài quy tắc tìm giới hạn vô cực 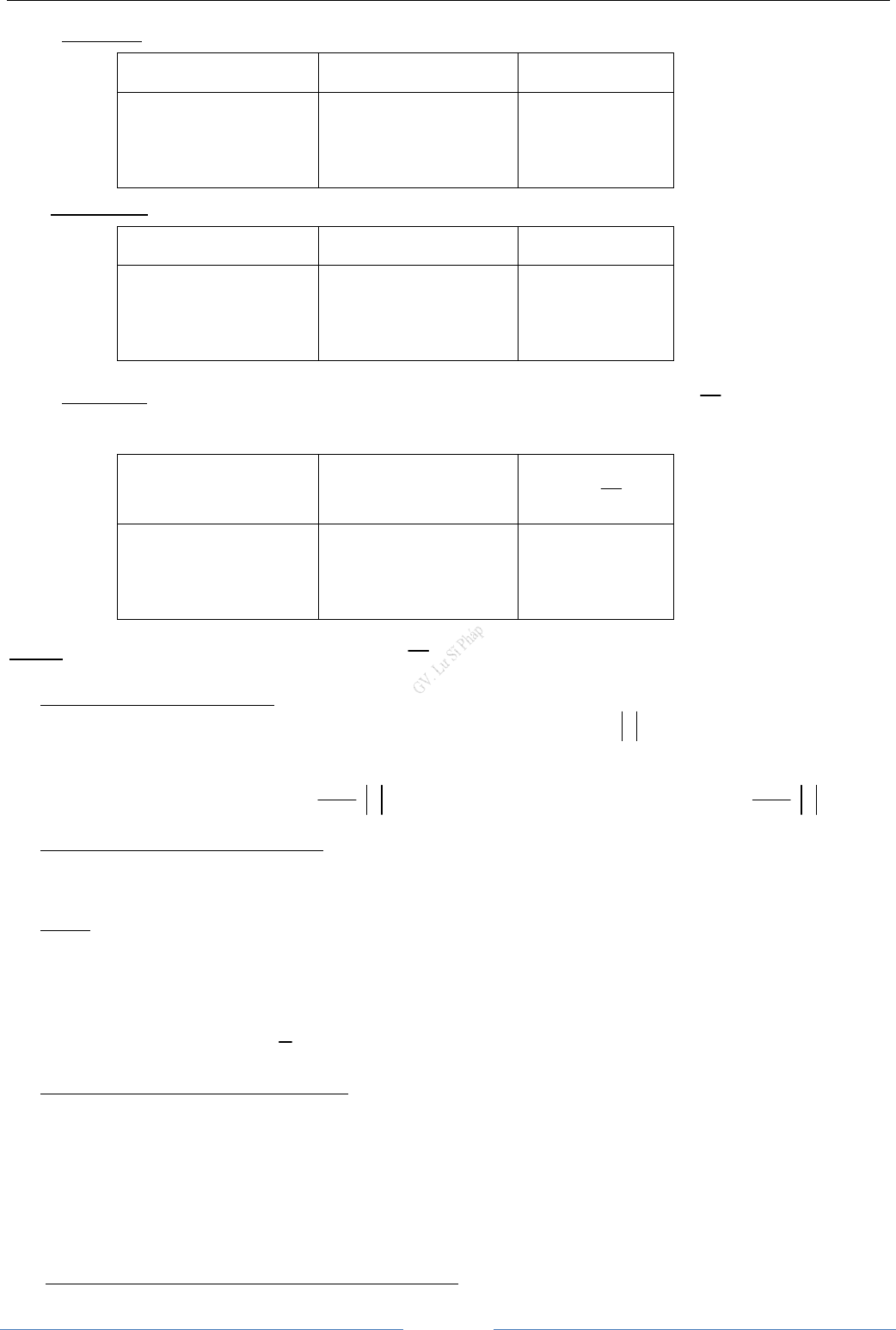Toán 11 GV. Lư Sĩ Pháp 2 BT. ĐS&GT 11 Chương IV. Giới hạn a) Quy tắc 1. Nếu nulim= ±∞ và nvlim= ±∞thì ()nnuvlim được cho trong bảng: nulim nvlim ()nnuvlim +∞ +∞ −∞ −∞ +∞ −∞ +∞ −∞ +∞ −∞ −∞ +∞ b) Quy tắc 2. Nếu nulim= ±∞ và nvLlim0=≠thì ()nnuvlim được cho trong bảng: nulim Dấu của L ()nnuvlim +∞ +∞ −∞ −∞ + − + − +∞ −∞ −∞ +∞ c) Quy tắc 3. . Nếu nuLlim0=≠ và nvlim0=và nv0> hoặc nv0< thì nnuvlim được cho trong bảng: Dấu của L Dấu của nv nnuvlim + + − − + − + − +∞ −∞ −∞ +∞ Chú ý . Nếu nnuLvlim0,lim=>=±∞ thì nnuvlim0= 6.Tổng cấp số nhân lùi vô hạn  Cấp số nhân lùi vô hạn là cấp số nhân có công bội q thỏa mãn q1<  Công thức tính tổng S của cấp số nhân lùi vô hạn (un) nuSuuuuqq1123......;11=+++++=<− hay nuSuu qu qu qqq2111111......;11−=+++++=<− 7. Định lí kẹp về giới hạn của dãy số Cho ba dãy số (un), (vn) ,(wn) và số thực L. Nếu nnnuvw≤≤với mọi n và lim un = lim wn = L thì dãy số (vn) có giới hạn và lim vn = L. 8. Lưu ý a) Dãy số tăng và bị chặn trên thì có giới hạn b) Dãy số giảm và bị chặn dưới thì có giới hạn c) Nếu limun = a thì limun + 1 = a d)Số e: nnen1lim1→+∞=+ 9.Phương pháp tìm giới hạn của dãy số - Vận dụng nội dung định nghĩa - Tìm giới hạn của một dãy số ta thường đưa về các giới hạn dạng đặc biệt và áp dụng các định lí về giới hạn hoặc các định lí về giới hạn vô cực:+ Nếu biểu thức có dạng phân thức mà mẫu và tử đều chứa các lũy thừa của n, thì chia tử và mẫu cho nk, với k là số mũ cao nhất.+ Nếu biểu thức có chứa n dưới dấu căn, thì có thể nhân tử số và mẫu số với cùng một biểu thức liên hợp. 10. Phương pháp tính tổng của cấp số nhân lùi vô hạn Chia sẻ bởi: Trịnh Thị Thanh

Tải về

Liên kết tải về Lý thuyết và bài tập chuyên đề giới hạn 1,3 MB Tải về Tìm thêm: Toán 11

Có thể bạn quan tâm

• 

  Tiếng Anh 6 Unit 5: Skills 1 - Soạn Anh 6 trang 54 sách Kết nối tri thức

  10.000+ 2
• 

  Đoạn văn tiếng Anh về lợi ích của học online (Dàn ý + 19 Mẫu)

  100.000+
• 

  Viết bản tin về hoạt động chào mừng ngày Nhà giáo Việt Nam ở trường

  10.000+
• 

  Kể lại truyền thuyết Sơn Tinh, Thủy Tinh bằng lời văn của em (2 Dàn ý + 22 mẫu)

  100.000+ 9
• 

  Văn mẫu lớp 11: Phân tích tác phẩm Cải ơi (Dàn ý + 3 Mẫu)

  10.000+
• 

  Đoạn văn tiếng Anh về sở thích nấu ăn (13 Mẫu)

  100.000+
• 

  Văn mẫu lớp 9: Đoạn văn nghị luận về tương thân tương ái (10 mẫu)

  100.000+ 1
• 

  Soạn bài Thực hành tiếng Việt trang 86 - Chân trời sáng tạo 7

  10.000+
• 

  Đoạn văn tiếng Anh về cách học tiếng Anh hiệu quả (Dàn ý + 14 Mẫu)

  100.000+
• 

  Viết đoạn văn nêu cảm nghĩ về một nhân vật trong một câu chuyện đã học (Dàn ý + 10 mẫu)

  100.000+ 9

Xem thêm

Nhiều người đang xem

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng! Xác thực ngay Số điện thoại này đã được xác thực! Bạn có thể dùng Sđt này đăng nhập tại đây! Lỗi gửi SMS, liên hệ Admin Sắp xếp theo Mặc định Mới nhất Cũ nhất Xóa Đăng nhập để Gửi KHO TÀI LIỆU GIÁO DỤC & HỖ TRỢ CAO CẤP

Hỗ trợ tư vấn

Tư vấn - Giải đáp - Hỗ trợ đặt tài liệu

Hotline

024 322 333 96

Khiếu nại & Hoàn tiền

Giải quyết vấn đề đơn hàng & hoàn trả

Mới nhất trong tuần

• Trả lời ngắn Toán 11: Phương trình lượng giác

  

• Trắc nghiệm đúng sai Toán 11: Giới hạn của hàm số

  

• Trắc nghiệm đúng sai Toán 11: Hàm số lượng giác

  

• Trắc nghiệm đúng sai Toán 11: Quan hệ song song trong không gian

  

• Trắc nghiệm đúng sai Toán 11: Phương trình lượng giác cơ bản

  

• Trả lời ngắn Toán 11: Hàm số lượng giác

  

• Trả lời ngắn Toán 11: Dãy số

  

• Trả lời ngắn Toán 11: Góc lượng giác

  

• Trả lời ngắn Toán 11: Giá trị lượng giác của góc lượng giác

  

• Trả lời ngắn Toán 11: Công thức lượng giác

  

Đóng Chỉ thành viên Download Pro tải được nội dung này! Download Pro - Tải nhanh, website không quảng cáo! Tìm hiểu thêm Mua Download Pro 79.000đ Nhắn tin Zalo

Tài khoản

Gói thành viên

Giới thiệu

Điều khoản

Bảo mật

Liên hệ

Facebook

Twitter

DMCA

Giấy phép số 569/GP-BTTTT. Bộ Thông tin và Truyền thông cấp ngày 30/08/2021. Cơ quan chủ quản: CÔNG TY CỔ PHẦN MẠNG TRỰC TUYẾN META. Địa chỉ: 56 Duy Tân, Phường Cầu Giấy, Hà Nội. Điện thoại: 024 2242 6188. Email: [email protected]. Bản quyền © 2025 download.vn.