Top 13+ Nghiệm Phương Trình Lượng Giác đặc Biệt - Gia Sư Điểm 10

Khi giải phương trình lượng giác chúng ta gặp rất nhiều bài toán đưa về dạng phương trình lượng giác đặc biêt như sinx=a,cosx=a,tanx=a,cotx=a. Bài này sẽ giải nghiệm cụ thể trong các trường hợp đặc biệt a=0,a=1,a=−1.

1. Phương trình lượng giác đặc biệt

Nghiệm của phương trình lượng giác đặc biệt sinx=0,1,−1

sinx=0⇔x=k.π,k∈Z

sinx=1⇔x=π2+k.2π,k∈Z

sinx=−1⇔x=−π2+k.2π,k∈Z

Nghiệm của phương trình lượng giác đặc biệt cosx=0,1,−1

cosx=0⇔x=π2+k.π,k∈Z

cosx=1⇔x=k.2π,k∈Z

cosx=−1⇔x=π+k.2π,k∈Z

Nghiệm của phương trình lượng giác đặc biệt tanx=0,1,−1

tanx=0⇔x=k.π,k∈Z

tanx=1⇔x=π4+k.π,k∈Z

Advertisement. Scroll to continue reading.

tanx=−1⇔x=−π4+k.π,k∈Z

Nghiệm của phương trình lượng giác đặc biệt cotx=0,1,−1

cotx=0⇔x=π2+k.π,k∈Z

cotx=1⇔x=π4+k.π,k∈Z

cotx=−1⇔x=−π4+k.π,k∈Z

>>Xem thêm: Tổng hợp công thức lượng giác đầy đủ.

2. Phương trình lượng giác cơ bản

Phương trình sinx = a

    ♦ |a| > 1: phương trình (1) vô nghiệm.

    ♦ |a| ≤ 1: gọi α là một cung thỏa mãn sinα = a.

Khi đó phương trình (1) có các nghiệm là

                x = α + k2π, k ∈ Z

                và x = π-α + k2π, k ∈ Z.

Nếu α thỏa mãn điều kiện 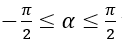 và sinα = a thì ta viết α = arcsin a.

Khi đó các nghiệm của phương trình (1) là

                x = arcsina + k2π, k ∈ Z

                và x = π – arcsina + k2π, k ∈ Z.

Phương trình cosx = a

    ♦ |a| > 1: phương trình (2) vô nghiệm.

    ♦ |a| ≤ 1: gọi α là một cung thỏa mãn cosα = a.

Khi đó phương trình (2) có các nghiệm là

                x = α + k2π, k ∈ Z

                và x = -α + k2π, k ∈ Z.

Nếu α thỏa mãn điều kiện 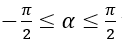 và cosα = a thì ta viết α = arccos a.

Khi đó các nghiệm của phương trình (2) là

                x = arccosa + k2π, k ∈ Z

                và x = -arccosa + k2π, k ∈ Z.

Phương trình tanx = a 

Điều kiện: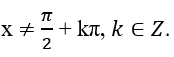 

Nếu α thỏa mãn điều kiện 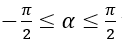 và tanα = a thì ta viết α = arctan a.

Khi đó các nghiệm của phương trình (3) là

                x = arctana + kπ,k ∈ Z

Phương trình cotx = a

Điều kiện: x ≠ kπ, k ∈ Z.

Nếu α thỏa mãn điều kiện 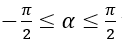 và cotα = a thì ta viết α = arccot a.

Khi đó các nghiệm của phương trình (4) là

                x = arccota + kπ, k ∈ Z

Chúc các bạn thành công!