Trắc Nghiệm Tìm Cực Trị Của Hàm Số Dựa Vào Bảng Biến Thiên, đồ Thị ...
Có thể bạn quan tâm
Trang chủNgữ văn Soạn văn 6 Soạn văn 7 Soạn văn 8 Soạn văn 9 Soạn Văn 10 Soạn văn 11 Soạn văn 12Văn mẫu Văn mẫu 6 Văn mẫu 7 Văn mẫu 8 Văn mẫu 9 Văn mẫu 10 Văn mẫu 11 Văn mẫu 12Thi vào 10 Tra điểm Tin tuyển sinh Điểm chuẩn Đề thi thử Đề thi đáp ánGiải đápTrắc nghiệmĐăng nhập Tạo tài khoảnĐăng Nhập với Email Đăng nhậpLấy lại mật khẩuĐăng Nhập với Facebook Google Apple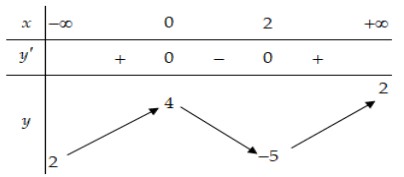 Mệnh đề nào dưới đây đúng? A. Hàm số đạt cực tiểu tại $x=-5$ B. Hàm số có bốn điểm cực trị C. Hàm số đạt cực tiểu tại $x=2$ D. Hàm số không có cực đại Câu 2. Cho hàm số $y=f(x)$ có bảng biến thiên như sau
Mệnh đề nào dưới đây đúng? A. Hàm số đạt cực tiểu tại $x=-5$ B. Hàm số có bốn điểm cực trị C. Hàm số đạt cực tiểu tại $x=2$ D. Hàm số không có cực đại Câu 2. Cho hàm số $y=f(x)$ có bảng biến thiên như sau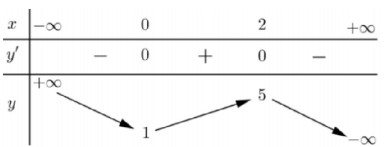 Giá trị cực đại của hàm số đã cho bằng A. 5 B. 2 C. 0 D. 1 Câu 3. Cho hàm số có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số đã cho là:
Giá trị cực đại của hàm số đã cho bằng A. 5 B. 2 C. 0 D. 1 Câu 3. Cho hàm số có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số đã cho là: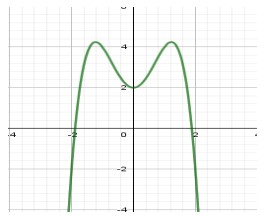 A. 3 B. 1 C. 2 D. 0 Câu 4. Cho hàm số $y=f(x)$ có bảng biến thiên như sau
A. 3 B. 1 C. 2 D. 0 Câu 4. Cho hàm số $y=f(x)$ có bảng biến thiên như sau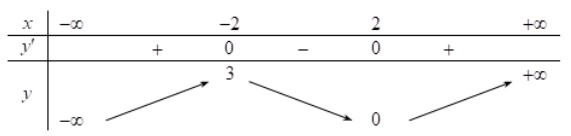 Tìm giá trị cực đại $y_{C D}$ và giá trị cực tiểu $y_{C T}$ của hàm số đã cho. A. $y_{C D}=2$ và $y_{C T}=0$ B. $y_{C D}=3$ và $y_{C T}=0$ C. $y_{C D}=3$ và $y_{C T}=-2$ D. $y_{C D}=-2$ và $y_{C T}=2$ Câu 5. Cho hàm số $f(x)$ có bảng biến thiên như sau:
Tìm giá trị cực đại $y_{C D}$ và giá trị cực tiểu $y_{C T}$ của hàm số đã cho. A. $y_{C D}=2$ và $y_{C T}=0$ B. $y_{C D}=3$ và $y_{C T}=0$ C. $y_{C D}=3$ và $y_{C T}=-2$ D. $y_{C D}=-2$ và $y_{C T}=2$ Câu 5. Cho hàm số $f(x)$ có bảng biến thiên như sau: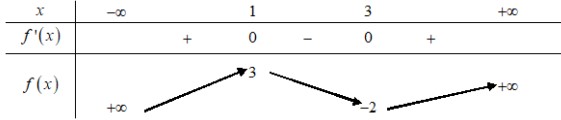 Hàm số đạt cực đại tại: A. $x=-2$. B. $x=3$ C. $x=1$ D. $x=2$. Câu 6. Cho hàm số $y=a x^{4}+b x^{2}+c(a, b, c \in \mathbb{R} )$ có đồ thị như hình vẽ bên.
Hàm số đạt cực đại tại: A. $x=-2$. B. $x=3$ C. $x=1$ D. $x=2$. Câu 6. Cho hàm số $y=a x^{4}+b x^{2}+c(a, b, c \in \mathbb{R} )$ có đồ thị như hình vẽ bên.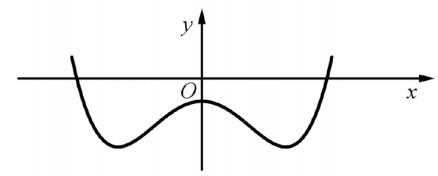 Số điểm cực trị của hàm số đã cho là A. 3 B. 0 C. 1 D. 2 Câu 7. Cho hàm số $f(x)$có bảng biến thiên như sau:
Số điểm cực trị của hàm số đã cho là A. 3 B. 0 C. 1 D. 2 Câu 7. Cho hàm số $f(x)$có bảng biến thiên như sau: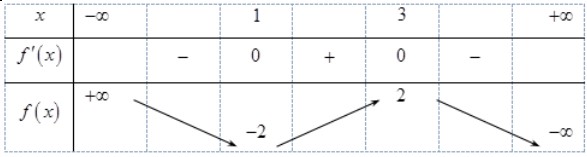 Hàm số đạt cực đại tại A. $x=-2$. B. $x=3$. C. $x=1$ D. $x=2$. Câu 8. Cho hàm số $y=f(x)$ có bảng biến thiên như sau
Hàm số đạt cực đại tại A. $x=-2$. B. $x=3$. C. $x=1$ D. $x=2$. Câu 8. Cho hàm số $y=f(x)$ có bảng biến thiên như sau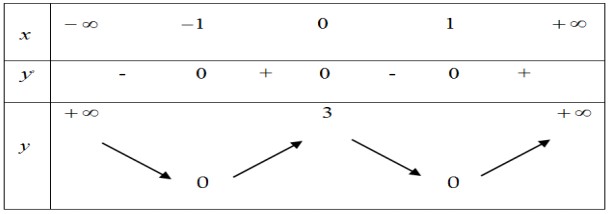 Mệnh đề nào dưới đây sai A. Hàm số có giá trị cực đại bằng 3 B. Hàm số có hai điểm cực tiểu C. Hàm số có giá trị cực đại bằng 0 D. Hàm số có ba điểm cực trị Câu 9. Cho hàm số $f(x)$ có bảng biến thiên như sau:
Mệnh đề nào dưới đây sai A. Hàm số có giá trị cực đại bằng 3 B. Hàm số có hai điểm cực tiểu C. Hàm số có giá trị cực đại bằng 0 D. Hàm số có ba điểm cực trị Câu 9. Cho hàm số $f(x)$ có bảng biến thiên như sau: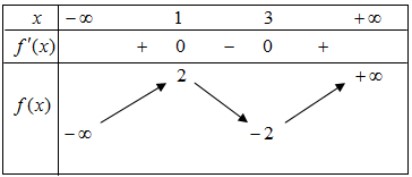 Hàm số đã cho đạt cực tiểu tại A. $x=2$. B. $x=-2$. C. $x=1$ D. $x=3$. Câu 10. Cho hàm số $y=a x^{3}+b x^{2}+c x+d(a, b, c, d \in \mathbb{R} )$ có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số này là
Hàm số đã cho đạt cực tiểu tại A. $x=2$. B. $x=-2$. C. $x=1$ D. $x=3$. Câu 10. Cho hàm số $y=a x^{3}+b x^{2}+c x+d(a, b, c, d \in \mathbb{R} )$ có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số này là 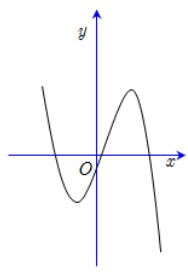 A. 3 B. 2 C. 0 D. 1 Câu 11. Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
A. 3 B. 2 C. 0 D. 1 Câu 11. Cho hàm số $y=f(x)$ có bảng biến thiên như sau: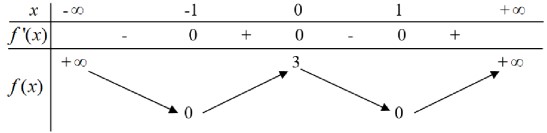 Hỏi hàm số nghịch biến trên khoảng nào sau đây? A. $(0 ; 1)$. B. $(1 ;+\infty)$. C. $(-1 ; 0)$. D. $(0 ;+\infty)$ Câu 12. Cho hàm số $f(x)$ có bảng biến thiên như sau:
Hỏi hàm số nghịch biến trên khoảng nào sau đây? A. $(0 ; 1)$. B. $(1 ;+\infty)$. C. $(-1 ; 0)$. D. $(0 ;+\infty)$ Câu 12. Cho hàm số $f(x)$ có bảng biến thiên như sau: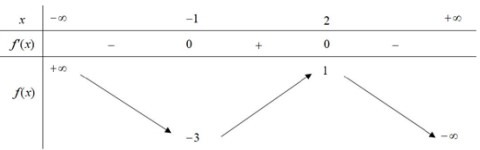 Hàm số đã cho đạt cực tiểu tại A. $x=-1$ B. $x=-3$. C. $x=2$. D. $x=1$. Câu 13. Cho hàm số $y=a x^{3}+b x^{2}+c x+d(a, b, c, d \in \mathbb{R} )$ có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số đã cho là
Hàm số đã cho đạt cực tiểu tại A. $x=-1$ B. $x=-3$. C. $x=2$. D. $x=1$. Câu 13. Cho hàm số $y=a x^{3}+b x^{2}+c x+d(a, b, c, d \in \mathbb{R} )$ có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số đã cho là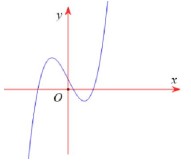 A. 2 B. 0 C. 3 D. 1 Câu 14. Cho hàm số $y=f(x)$ có bảng biến thiên như sau
A. 2 B. 0 C. 3 D. 1 Câu 14. Cho hàm số $y=f(x)$ có bảng biến thiên như sau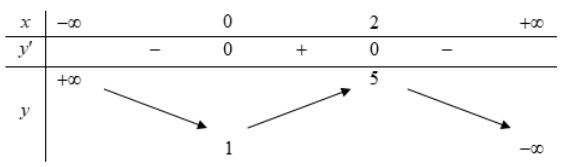 Hàm số đạt cực đại tại điểm A. $x=1$ B. $x=0$ C. $x=5$ D. $x=2$ Câu 15. Cho hàm số $y=f(x)$ xác định, liên tục trên đoạn $[-2 ; 2]$ và có đồ thị là đường cong trong hình vẽ bên. Hàm số $f(x)$ đạt cực đại tại điểm nào dưới đây
Hàm số đạt cực đại tại điểm A. $x=1$ B. $x=0$ C. $x=5$ D. $x=2$ Câu 15. Cho hàm số $y=f(x)$ xác định, liên tục trên đoạn $[-2 ; 2]$ và có đồ thị là đường cong trong hình vẽ bên. Hàm số $f(x)$ đạt cực đại tại điểm nào dưới đây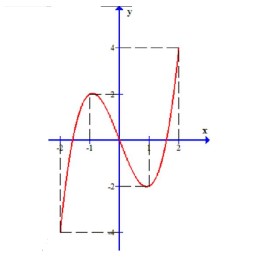 A. $x=-2$. B. $x=-1$ C. $x=1$ D. $x=2$
A. $x=-2$. B. $x=-1$ C. $x=1$ D. $x=2$





Tạo tài khoản Doctailieu
Để sử dụng đầy đủ tính năng và tham gia cộng đồng của chúng tôi Tạo tài khoảnTạo tài khoản với Facebook Google AppleKhi bấm tạo tài khoản bạn đã đồng ý với quy định của tòa soạnLấy lại mật khẩuNhập Email của bạn để lấy lại mật khẩu Lấy lại mật khẩu Trang chủTrắc nghiệm Luyện Thi THPTTrắc nghiệm môn Toán Luyện Thi THPT
Bài tập trắc nghiệm ôn tâp tìm cực trị của hàm số dựa vào bảng biến thiên, đồ thị của hàm số đó có đáp án giúp các bạn rè luyện.
Danh sách câu hỏi Đáp ánCâu 1. Cho hàm số $y=f(x)$ có bảng biến thiên như sau Mệnh đề nào dưới đây đúng? A. Hàm số đạt cực tiểu tại $x=-5$ B. Hàm số có bốn điểm cực trị C. Hàm số đạt cực tiểu tại $x=2$ D. Hàm số không có cực đại Câu 2. Cho hàm số $y=f(x)$ có bảng biến thiên như sau
Mệnh đề nào dưới đây đúng? A. Hàm số đạt cực tiểu tại $x=-5$ B. Hàm số có bốn điểm cực trị C. Hàm số đạt cực tiểu tại $x=2$ D. Hàm số không có cực đại Câu 2. Cho hàm số $y=f(x)$ có bảng biến thiên như sau Giá trị cực đại của hàm số đã cho bằng A. 5 B. 2 C. 0 D. 1 Câu 3. Cho hàm số có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số đã cho là:
Giá trị cực đại của hàm số đã cho bằng A. 5 B. 2 C. 0 D. 1 Câu 3. Cho hàm số có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số đã cho là: A. 3 B. 1 C. 2 D. 0 Câu 4. Cho hàm số $y=f(x)$ có bảng biến thiên như sau
A. 3 B. 1 C. 2 D. 0 Câu 4. Cho hàm số $y=f(x)$ có bảng biến thiên như sau Tìm giá trị cực đại $y_{C D}$ và giá trị cực tiểu $y_{C T}$ của hàm số đã cho. A. $y_{C D}=2$ và $y_{C T}=0$ B. $y_{C D}=3$ và $y_{C T}=0$ C. $y_{C D}=3$ và $y_{C T}=-2$ D. $y_{C D}=-2$ và $y_{C T}=2$ Câu 5. Cho hàm số $f(x)$ có bảng biến thiên như sau:
Tìm giá trị cực đại $y_{C D}$ và giá trị cực tiểu $y_{C T}$ của hàm số đã cho. A. $y_{C D}=2$ và $y_{C T}=0$ B. $y_{C D}=3$ và $y_{C T}=0$ C. $y_{C D}=3$ và $y_{C T}=-2$ D. $y_{C D}=-2$ và $y_{C T}=2$ Câu 5. Cho hàm số $f(x)$ có bảng biến thiên như sau: Hàm số đạt cực đại tại: A. $x=-2$. B. $x=3$ C. $x=1$ D. $x=2$. Câu 6. Cho hàm số $y=a x^{4}+b x^{2}+c(a, b, c \in \mathbb{R} )$ có đồ thị như hình vẽ bên.
Hàm số đạt cực đại tại: A. $x=-2$. B. $x=3$ C. $x=1$ D. $x=2$. Câu 6. Cho hàm số $y=a x^{4}+b x^{2}+c(a, b, c \in \mathbb{R} )$ có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số đã cho là A. 3 B. 0 C. 1 D. 2 Câu 7. Cho hàm số $f(x)$có bảng biến thiên như sau:
Số điểm cực trị của hàm số đã cho là A. 3 B. 0 C. 1 D. 2 Câu 7. Cho hàm số $f(x)$có bảng biến thiên như sau: Hàm số đạt cực đại tại A. $x=-2$. B. $x=3$. C. $x=1$ D. $x=2$. Câu 8. Cho hàm số $y=f(x)$ có bảng biến thiên như sau
Hàm số đạt cực đại tại A. $x=-2$. B. $x=3$. C. $x=1$ D. $x=2$. Câu 8. Cho hàm số $y=f(x)$ có bảng biến thiên như sau Mệnh đề nào dưới đây sai A. Hàm số có giá trị cực đại bằng 3 B. Hàm số có hai điểm cực tiểu C. Hàm số có giá trị cực đại bằng 0 D. Hàm số có ba điểm cực trị Câu 9. Cho hàm số $f(x)$ có bảng biến thiên như sau:
Mệnh đề nào dưới đây sai A. Hàm số có giá trị cực đại bằng 3 B. Hàm số có hai điểm cực tiểu C. Hàm số có giá trị cực đại bằng 0 D. Hàm số có ba điểm cực trị Câu 9. Cho hàm số $f(x)$ có bảng biến thiên như sau: Hàm số đã cho đạt cực tiểu tại A. $x=2$. B. $x=-2$. C. $x=1$ D. $x=3$. Câu 10. Cho hàm số $y=a x^{3}+b x^{2}+c x+d(a, b, c, d \in \mathbb{R} )$ có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số này là
Hàm số đã cho đạt cực tiểu tại A. $x=2$. B. $x=-2$. C. $x=1$ D. $x=3$. Câu 10. Cho hàm số $y=a x^{3}+b x^{2}+c x+d(a, b, c, d \in \mathbb{R} )$ có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số này là  A. 3 B. 2 C. 0 D. 1 Câu 11. Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
A. 3 B. 2 C. 0 D. 1 Câu 11. Cho hàm số $y=f(x)$ có bảng biến thiên như sau: Hỏi hàm số nghịch biến trên khoảng nào sau đây? A. $(0 ; 1)$. B. $(1 ;+\infty)$. C. $(-1 ; 0)$. D. $(0 ;+\infty)$ Câu 12. Cho hàm số $f(x)$ có bảng biến thiên như sau:
Hỏi hàm số nghịch biến trên khoảng nào sau đây? A. $(0 ; 1)$. B. $(1 ;+\infty)$. C. $(-1 ; 0)$. D. $(0 ;+\infty)$ Câu 12. Cho hàm số $f(x)$ có bảng biến thiên như sau: Hàm số đã cho đạt cực tiểu tại A. $x=-1$ B. $x=-3$. C. $x=2$. D. $x=1$. Câu 13. Cho hàm số $y=a x^{3}+b x^{2}+c x+d(a, b, c, d \in \mathbb{R} )$ có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số đã cho là
Hàm số đã cho đạt cực tiểu tại A. $x=-1$ B. $x=-3$. C. $x=2$. D. $x=1$. Câu 13. Cho hàm số $y=a x^{3}+b x^{2}+c x+d(a, b, c, d \in \mathbb{R} )$ có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số đã cho là A. 2 B. 0 C. 3 D. 1 Câu 14. Cho hàm số $y=f(x)$ có bảng biến thiên như sau
A. 2 B. 0 C. 3 D. 1 Câu 14. Cho hàm số $y=f(x)$ có bảng biến thiên như sau Hàm số đạt cực đại tại điểm A. $x=1$ B. $x=0$ C. $x=5$ D. $x=2$ Câu 15. Cho hàm số $y=f(x)$ xác định, liên tục trên đoạn $[-2 ; 2]$ và có đồ thị là đường cong trong hình vẽ bên. Hàm số $f(x)$ đạt cực đại tại điểm nào dưới đây
Hàm số đạt cực đại tại điểm A. $x=1$ B. $x=0$ C. $x=5$ D. $x=2$ Câu 15. Cho hàm số $y=f(x)$ xác định, liên tục trên đoạn $[-2 ; 2]$ và có đồ thị là đường cong trong hình vẽ bên. Hàm số $f(x)$ đạt cực đại tại điểm nào dưới đây A. $x=-2$. B. $x=-1$ C. $x=1$ D. $x=2$
A. $x=-2$. B. $x=-1$ C. $x=1$ D. $x=2$ đáp án Trắc nghiệm tìm cực trị của hàm số dựa vào bảng biến thiên, đồ thị của hàm số đó
| Câu | Đáp án | Câu | Đáp án |
|---|---|---|---|
| Câu 1 | C | Câu 9 | D |
| Câu 2 | A | Câu 10 | B |
| Câu 3 | A | Câu 11 | A |
| Câu 4 | B | Câu 12 | A |
| Câu 5 | C | Câu 13 | A |
| Câu 6 | A | Câu 14 | D |
| Câu 7 | B | Câu 15 | B |
| Câu 8 | C |
Bài toán cực trị của số phức với các dạng câu hỏi quen thuộc

Đáp án đề thi Toán mã đề 109 THPT Quốc Gia 2021

Đáp án đề thi Toán mã đề 101 THPT Quốc Gia 2021

Đề minh họa 2021 môn Toán kỳ thi tốt nghiệp THPT Quốc Gia (có đáp án)

Đề luyện thi tốt nghiệp THPT môn Toán số 11 có đáp án

Đề đánh giá năng lực ĐHQG-HCM năm 2021 phần 2 (đề mẫu)
XTừ khóa » Tìm Cực Trị Của Hàm Số Dựa Vào đồ Thị
-
Tìm Cực Trị Của Hàm Số Dựa Vào đồ Thị Cực Hay, Có Lời Giải
-
Dạng Bài Tìm Cực Trị Của Hàm Số Dựa Vào Bảng Biến Thiên, đồ Thị Của ...
-
Cực Trị Của Hàm Số | Lý Thuyết & Phân Dạng Bài Tập (Kèm Tài Liệu)
-
Cách Tìm Cực Trị Của Hàm Hợp Cực Hay, Có Lời Giải - Toán Lớp 12
-
Đếm Số điểm Cực Trị Dựa Vào Bảng Biến Thiên Hoặc đồ Thị
-
Tìm Cực Trị Của Hàm Số F(x) Và Hàm Hợp F(u(x)) Bằng đồ Thị(P2)
-
Cực Trị Của Hàm Số Là Gì ? Quy Tắc Và Hướng Dẫn Cách Tìm Cực Trị ...
-
Cực Trị Của Hàm Số: Chi Tiết Lý Thuyết Và Các Dạng Bài Tập Thường Gặp
-
Tìm Cực Trị Của Hàm Số Hợp F(u(x)) Khi Biết đồ Thị Hàm Số F(x) - 123doc
-
Cực Trị Của Hàm Số Lớp 12: Lý Thuyết, Cách Tìm Và Các Dạng Bài ...
-
2 Cách Tìm Cực Trị Của Hàm Số Siêu Nhanh
-
Dựa Vào Bảng Xét Dấu Của F'(x) / Cho Hàm Số F'(x ...
-
Cực Trị Của Hàm Số