Trang 3 | Maths 4 Physics & More...

Có thể bạn quan tâm

Maths 4 Physics & more…

Blog Toán Cao Cấp (M4Ps)

Tìm

Search for: Đi

Author
Bài viết
Bài giảng
- Giải tích 1
  - Hàm số – Hàm lượng giác ngược – Hàm hyperbol
  - Chia một đa thức cho tam thức bậc 2
  - Giới hạn của hàm số (Limit of a function)
  - Vô cùng bé (infinitesimal)
  - Đạo hàm và vi phân của hàm số (derivative and differential of a function)
  - Khai triển Taylor – Maclaurin (Taylor expansion)
  - Khảo sát đường cong tham số
  - Tích phân hữu tỷ (integration by partial fractions)
  - Tích phân hàm vô tỉ (Integrals involving roots)
  - Tích phân suy rộng (Improper Integrals)
  - Chuỗi số. Tổng của chuỗi (Series. The total sum of series)
  - Chuỗi số dương (Infinitive Series)
  - Chuỗi Fourier
  - Chuỗi Fourier Sine và Cosine
- Giải tích 2
  - Khái niệm mở đầu về hàm nhiều biến
  - Giới hạn của hàm hai biến số
  - Đạo hàm riêng
  - Hàm số khả vi và vi phân toàn phần
  - Đạo hàm của hàm hợp
  - Đạo hàm hàm số ẩn
  - Cực trị (không điều kiện) của hàm 2 biến
  - Cực trị có điều kiện (cực trị ràng buộc)
  - Các khái niệm cơ bản của phương trình vi phân
  - Phương trình tách biến, phương trình đẳng cấp cấp 1
  - Phương trình vi phân tuyến tính cấp 1, Bernoulli, Ricatti
  - Phương trình vi phân tuyến tính cấp 2 (linear second-order ordinary differential equation)
  - Ứng dụng chuỗi số giải phương trình vi phân
  - Tích phân hai lớp (Tích phân kép)
  - Tích phân hai lớp trong tọa độ cực. Công thức đổi biến
  - Tích phân đường theo tọa độ (Tp đường loại 2)
  - Số phức (Complex Number)
- Đại số tuyến tính (Linear Algebra)
  - Tập hợp
  - Khái niệm về ma trận
  - Ma trận bậc thang (Echelon matrix)
  - Ma trận nghịch đảo (khả nghịch)
  - Thuật toán tìm ma trận bậc thang
  - Định thức (Determinants)
  - Hệ phương trình tuyến tính (System of Linear Equations)
  - Khái niệm về ánh xạ tuyến tính
  - Không gian vectơ Euclide (Euclidean Vector Spaces)
  - Trị riêng, vectơ riêng của ma trận (Eigenvalues and Eigenvectors)
  - Dạng toàn phương
- Xác suất thống kê
  - Bổ túc về Giải tích Tổ hợp
  - Biến cố và quan hệ giữa các biến cố
  - Các định nghĩa của xác suất
  - Xác suất có điều kiện
  - Đại lượng ngẫu nhiên 1 chiều
  - Một số quy luật phân phối xác suất rời rạc
  - Ước lượng tham số của tổng thể
  - Kiểm định giả thiết
- Phương pháp Toán Lý (PT Đạo hàm riêng và PBĐ Laplace)
  - Phép biến đổi Laplace – Các khái niệm mở đầu
Bài tập
Trắc nghiệm
Thảo luận
- Thảo luận (tiếp theo)
- Thảo luận chung (tt)
- Thảo luận về giải tích
  - Thảo luận Giải tích – Trang 2
- Thảo luận ĐSTT
  - Trang 2
  - Trang 3
- Thảo luận XSTK
  - Trang 2
- Thảo luận về tích phân bội
Đề thi
Ebooks
- Maths Ebooks
  - Giải tích – Đại số
  - XSTK – Phương pháp tính
  - Hàm phức – PDEs
  - Tài liệu khác
- Giáo dục – Khoa học
- Thư giãn
Một thời để nhớ
Softwares
Links
Sitemap

Trang 3

Đánh giá:

Chia sẻ:

In
PDF
Email
Facebook

Thích Đang tải...

Thảo luận

62 bình luận về “Trang 3”

Da dung thua thay, bai xet ma tran duong cheo nxn co dang Ta= … o tren la thuoc ve mon phuong phap tinh. Em dang bi bai nay, mong thay vui long giang cho em voi CAM ON THAY NHIEU LAM!!!

ThíchThích
Được đăng bởi hoang linh | 20/08/2009, 11:54 Reply to this comment
thầy có thể vui lòng giảng cho em bài này với Xét một ma trận đường chéo nxn có dạng: $Ta = \left[\begin{array}{rrrrrrrr} a & -1 & 0 & 0 & ... & 0 & 0 & 0 \\ -1 & a & -1 & 0 & ... & 0 & 0 & 0 \\ 0 & -1 & a & -1 & ... & 0 & 0 & 0 \\ ... & ... & ... & ... & ... & ... & ... & ... \\ 0 & 0 & 0 & 0 & ... & -1 & a & -1 \\ 0 & 0 & 0 & 0 & ... & 0 & -1 & a \\ \end{array} \right]$ Trong đó a là số thực a. Kiểm tra để các giá trị riêng của Ta cho bởi: ${\lambda}_j = a - 2cos(j.{\varphi})$ với $j = \overline{1,n} , \varphi = \dfrac{n}{\pi} + 1$ . b. Cho a = 2 i. Phép lặp Jacobi có hội tụ với ma trận này không. ii. Phép lặp Gauss- Seidel có hội tụ với ma trận này không.

ThíchThích
Được đăng bởi hoang linh | 19/08/2009, 16:39 Reply to this comment
- Phần này thuộc phần Giải tích số (Phương pháp tính) đúng không em?
  
  ThíchThích
  Được đăng bởi 2Bo02B | 19/08/2009, 22:07 Reply to this comment
Em chưa hiểu lắm về không gian cột Col A. Thầy có thể cho em 1 VD để hiểu rõ hơn

ThíchThích
Được đăng bởi minh trung | 10/03/2009, 15:15 Reply to this comment
- Nói nôm na không gian cột là không gian sinh bởi các vecto cột. Các vecto cột là cac vecto có các thành phần viết theo dạng cột. Ví dụ: vecto (a,b,c) được gọi là vecto hàng. Nhưng nếu viết là: $\left(\begin{array}{c} a \\ b \\ c \\ \end{array} \right)$ thì gọi là vecto cột Các khái niệm này dùng để tìm mối tương ứng giữa các kết quả của ma trận và không gian vecto.
  
  ThíchThích
  Được đăng bởi 2Bo02B | 10/03/2009, 21:49 Reply to this comment
vậy chắc bằng nhau hả thầy

ThíchThích
Được đăng bởi quanghung | 03/03/2009, 16:58 Reply to this comment
- Bằng nhau chính là trùng nhau đó em. Bài này chắc cho sai 1 vecto nào đó rồi. Có thể u3=(-1,1,-2) chứ hok phải (-1,1,2)
  
  ThíchThích
  Được đăng bởi 2Bo02B | 03/03/2009, 17:11 Reply to this comment
Đặc trưng của 1 kgvt là cơ sở và số chiều của nó. Vì vậy, nếu 2 kgvt sinh bởi 2 hệ vecto mà hai hệ này có số vecto khác nhau thì để 2 kgvt đó trùng nhau thì chỉ cần chúng có cùng số chiều và cơ sở là được. Điều lạ là với giả thiết của bạn thì dimU = 3 (vì 3 vecto u1, u2, u3 đltt), còn dimV = 2. Lạ quá! Chắc đề sai quá. Em mong Thầy giải đáp giúp

ThíchĐã thích bởi 1 người
Được đăng bởi Vũ Hoàng | 03/03/2009, 15:54 Reply to this comment
- Có lẽ đề bài cho sai rồi em à. Hai không gian có số chiều khác nhau thì không thể trùng nhau được
  
  ThíchThích
  Được đăng bởi 2Bo02B | 03/03/2009, 16:14 Reply to this comment
bài này thấy lạ quá thầy ơi ( u cho 3 vec tơ mà v chỉ cho có 2 vec tơ thôi) cho u= {u1=(1,1,1) ; u2=(3,1,4) ; u3=(-1,1,2)} , v = {v1=(1,-1,2) ; v2=(5,3,6)} Chứng minh rằng u và w là 2 không gian vec tơ trùng nhau.

ThíchThích
Được đăng bởi quanghung | 03/03/2009, 13:35 Reply to this comment
bạn có thể giải thích kỹ phần này không vậy:

“Như vậy, U+V là 1 kg sinh bởi hệ 4 vecto trên. Tìm bộ phận đltt tối đại của hệ 4 vecto đó bạn sẽ có 3 vecto. Và hệ 3 vecto này đltt, sinh ra U + V nên nó là 1 cơ sở của U + V”

ThíchThích
Được đăng bởi quanghung | 01/03/2009, 22:00 Reply to this comment
- Bạn Vũ Hoàng đã chính xác. Em chú ý định nghĩa của U + V. Ta có: $U + V = \{x : x = u + v, u \in U, v \in V \}$ Do U có cơ sở là (1,0,1) , (-2,1,0) nên u = a(1,0,1) + b(-2,1,0) . Tương tự V có cơ sở là 2 vecto (1,2,0) , (0,1,1) nên v = c (1,2,0) + d(0,1,1) Vậy U + V = a(1,01) + b(-2,1,0) + c(1,2,0) + d(0,1,1) Điều này chứng tỏ 4 vecto trên sinh ra U + V. Mà 1 hệ vecto muốn làm cơ sở của 1 kg thì hệ đó phải là hệ sinh và đltt nên từ hệ sinh của U + V, ta tìm bộ phận độc lập tuyến tính tối đại thì đó chính là cơ sở của U + V.
  
  ThíchThích
  Được đăng bởi 2Bo02B | 01/03/2009, 22:19 Reply to this comment
Bài này bạn chỉ cần chứng minh dim(U+V) = 3 là xong. Vì khi đó, cơ sở của U+V là 3 vecto đltt trong R3 nên nó cũng là cơ sở của R3. Hai không gian có số chiều, cùng cơ sở thì trùng nhau. Từ U bạn tìm được 2 vecto (1,0,1) , (-2,1,0) là 1 cơ sở của U. Tương tự bạn có 2 vecto (1,2,0) , (0,1,1) là 1 cơ sở của V. Như vậy, U+V là 1 kg sinh bởi hệ 4 vecto trên. Tìm bộ phận đltt tối đại của hệ 4 vecto đó bạn sẽ có 3 vecto. Và hệ 3 vecto này đltt, sinh ra U + V nên nó là 1 cơ sở của U + V.

ThíchThích
Được đăng bởi Vũ Hoàng | 01/03/2009, 16:56 Reply to this comment
trong không gian R3 cho hai không gian con: $U = \{(x1, x2, x3) \in R_3 : x_1+2x_2-x_3 =0 \}$ $V = \{(x1, x2, x3) \in R_3 : 2x_1-x_2+x_3 =0 \}$ chứng minh rằng : U + V = R3

ThíchThích
Được đăng bởi quanghung | 01/03/2009, 12:42 Reply to this comment
- Thầy ơi! khi tìm được trang web nay em như mèo mù vớ cá ráng mong thầy và các bạn giúp dùm em. Cho ma trận ( m 1 1 1 ) A=( 1 m 1 1 ) ( 1 1 1 m^2) Tìm`các giá trị của m để r(A)<3. Với bài này mình có phải xét tất cả các định thức con cấp 3 để chúng bằng 0 hết không ạ!
  
  ThíchThích
  Được đăng bởi Nguyenbao | 15/01/2010, 18:07 Reply to this comment
thầy ơi cho em hỏi cách tìm ker(f) và Im (f) nha .thầy có thể giải cụ thể cho em một bài nay nha : Cho ánh xạ f : R4……….> R4 f(x1,x2,x3,x4)= (x1+x2,x3+x4) tìm ker (f) và Im (f)

ThíchThích
Được đăng bởi ngô minh thái | 14/02/2009, 20:49 Reply to this comment
- Để giải bài này, em cần chú ý thế nào là Ker(f) , Im(f): Cho ánh xạ tuyến tính $f: X \to Y$ . Khi đó: $Ker(f) = \{x \in X: f(x) = 0 \} ;\\ Im(f) = \{y \in Y: \exists x \in X, f(x) = y \}$ Và mối liêm hệ giữa ker(f), Im(f) là: $dim(ker(f))+dim(Im(f)) = dim X$ Như vậy, để tìm ker(f) em chỉ cần giải hpt f(x) = 0. Với bài trên ta có: $kerf = \{(x_1,x_2,x_3,x_4): x_1 + x_2 = 0, x_3 + x_4=0 \}$ Vậy em có: $x_1 = a, x_2 = -a, x_3 = b, x_4 = -b$ Do đó: $kerf = \{a(1,-1,0,0)+b(0,0,1,-1): a,b \in R \}$ Như vậy: dim(kerf) = 2 và cơ sở của kerf là: (1,-1,0,0) và (0,0,1,-1)
  
  Từ kết quả này, theo nhận xét ở trên, em sẽ có dim(imf) = 2. Để tìm Imf, ta tìm $(x;y) \in R^2$ sao cho $\exists (x_1,x_2,x_3,x_4)$ để $f(x_1,x_2,x_3,x_4) = (x;y)$ Tuy nhiên, từ công thức xác định ánh xạ f ta có: $(x;y) = (x_1+x_2;x_3+x_4)$ nên ta có thể viết ánh xạ f dưới dạng sau: $f(x_1,x_2,x_3,x_4) = x_1(1, 0) + x_2(1,0) + x_3(0;1) +x_4(0;1)$ Vậy Imf sinh bởi các vecto (1;0) , (1;0) , (0;1) , (0;1) Sử dụng cách tìm cơ sở của 1 hệ vecto, ta sẽ có dim(imf) = 2, và 1 cơ sở của Imf là (1;0), (0,;1). Điều này nghĩa là Imf trùng với $R^2$
  
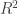
  ThíchThích
  Được đăng bởi 2Bo02B | 15/02/2009, 06:42 Reply to this comment
Mình không biết x1, x2 là gì cả. Sao không thấy bạn đề cập đến vậy.

ThíchThích
Được đăng bởi Vũ Hoàng | 13/01/2009, 17:08 Reply to this comment
Thầy giúp em bài này: C/m: bộ 3 vector bất kì rút từ {w1,w2,w3,w4} đều phụ thuộc tt, biết span {w1,w2,w3,w4}= span{x1,x2}

ThíchThích
Được đăng bởi PADũng | 12/01/2009, 23:10 Reply to this comment

« Bình luận cũ hơn Bình luận mới hơn »

Bình luận về bài viết này Hủy trả lời

Translators & RSS

Maths 4 Physics (M4Ps)

Đăng ký nhận tin

Bạn hãy nhập địa chỉ email của mình để đăng ký theo dõi tin tức từ blog này và nhận những bài viết mới nhất qua địa chỉ email.

Tham gia cùng 2 793 người đăng ký khác

Đôi lời

Bạn có thể theo dõi các lời bình liên quan đến lời bình của mình qua email bằng cách chọn dòng thông báo Báo cho bạn khi có người bình luận tiếp theo đề tài này bằng điện thư mỗi khi viết 1 lời bình.

Rất mong các bạn viết lời nhắn bằng tiếng việt có dấu nhé.

Để viết tiếng việt có dấu bạn dùng font chữ Unicode và bảng mã là Unicode UTF-8.

Để biết cách gõ công thức Toán học trong các lời nhắn ở trang web này, mời bạn đọc bài hướng dẫn tại đây hoặc bạn có thể xem bài hướng dẫn dùng MathType tại đây và bài tạo công thức trực tuyến tại đây

Get Well

Lời nhắn mới nhất

	Dương Khánh Uyên trong Trang 2
	Trần Thái An trong Trang 2
	Chúc Chúc trong Xác suất có điều kiện
	Hoang Anh trong Khai triển Taylor – Macl…
	Trần Trung Đức trong Mẹo phân tích nhanh 1 phân…
	Nhung Duong trong Trang 2
	khoi trong Khai triển Taylor – Macl…
	Minh pham trong Chuỗi Fourier Sine và Cos…
	Minh Phạm trong Chuỗi Fourier
	Anh Tuấn trong Cực trị (không điều kiện) của…

Bài “hot”

Khai triển Taylor - Maclaurin (Taylor expansion)
Phương trình vi phân tuyến tính cấp 1, Bernoulli, Ricatti
Cực trị có điều kiện (cực trị ràng buộc)
Ma trận nghịch đảo (khả nghịch)
Phương trình tách biến, phương trình đẳng cấp cấp 1
Cực trị (không điều kiện) của hàm 2 biến
Chuỗi số. Tổng của chuỗi (Series. The total sum of series)
Đạo hàm hàm số ẩn
Khái niệm về ma trận
Phương trình vi phân tuyến tính cấp 2 (linear second-order ordinary differential equation)

Bài viết chuyên đề

Bài giảng (20)
- Video bài giảng (4)
Bài viết (192)
- Bài viết về ICT (59)
  - Cảnh báo virus (1)
  - giaovien.net (6)
  - Mẹo Wordpress (13)
  - Thủ thuật Gmail (7)
- Giáo dục (29)
- Khoa học (51)
- Thư giãn (45)
Bí quyết học tập (20)
Cuộc sống sinh viên (26)
Hình ảnh và Tin tức (32)
Làm theo lời Bác (9)
Life's Art (61)
nguyên tắc sáng tạo (27)
Toán học (104)
- Lịch sử Toán học (13)
- Liên kết Toán học (6)
- Luyện thi Đại học (7)
  - Đề thi thử (4)
- Vẻ đẹp Toán học (8)
- Đố vui (36)

Maths 4 Physics & more…

Tạo một blog miễn phí với WordPress.com.

Trang này sử dụng cookie. Tìm hiểu cách kiểm soát ở trong: Chính Sách Cookie

Theo dõi Đã theo dõi
- Maths 4 Physics & more...
- Đã có tài khoản WordPress.com? Đăng nhập.
- Maths 4 Physics & more...
- Theo dõi Đã theo dõi
- Đăng ký
- Đăng nhập
- URL rút gọn
- Báo cáo nội dung
- Xem toàn bộ bài viết
- Quản lý theo dõi
- Ẩn menu

%d Tạo trang giống vầy với WordPress.comHãy bắt đầu

Từ khóa » Cách Chứng Minh Không Gian Vecto Con

Trang 3 | Maths 4 Physics & More...

Maths 4 Physics & more…

Tìm

Đánh giá:

Chia sẻ:

Thảo luận

62 bình luận về “Trang 3”

Bình luận về bài viết này Hủy trả lời

Translators & RSS

Đăng ký nhận tin

Đôi lời

Lời nhắn mới nhất

Bài “hot”

Bài viết chuyên đề

CHỨNG MINH KHÔNG GIAN CON VÀ TÌM CƠ SỞ SỐ CHIỀU CỦA ...

GIẢI BÀI TẬP CHỨNG MINH KHÔNG GIAN VECTƠ CON TÌM CƠ ...

Không Gian Vectơ Con - YouTube

Bài 4: Không Gian Vectơ Con - Hoc247

Phương Pháp Chứng Minh Tập Hợp L Là Không Gian Con Của Không ...

Không Gian Vecto Con – Bài Tập Và Lời Giải - TTnguyen

Chứng Minh Không Gian Vecto Con

[Top Bình Chọn] - Chứng Minh Không Gian Vecto Con - Trần Gia Hưng

[PDF] Chương II KHÔNG GIAN VECTƠ MỞ ÐẦU Trong Chương I Ta đã ...

Hướng Dẫn Giải Bài Tập Không Gian Véc Tơ đại Số Tuyến Tính , đề Thi ...

[PDF] Bài 5 : KHÔNG GIAN VÉCTƠ - Topica

BAI TAP Chuong 4 - Không GIAN VECTƠ - StuDocu

Cơ Sở Của Không Gian Véctơ | Học Toán Online Chất Lượng Cao 2022

Liên Hệ