Trị Riêng, Vectơ Riêng Của Ma Trận (Eigenvalues And Eigenvectors)

Có thể bạn quan tâm

Shortlink: http://wp.me/P8gtr-tp

I. Trị riêng, vectơ riêng:

1.1 Định nghĩa: Cho A là ma trận vuông cấp n trên trường số $K (K = \mathbb{R}; \mathbb{C})$ . Số $\lambda \in K$ được gọi là giá trị riêng (gọi tắt là trị riêng – kí hiệu GTR) của ma trận A, nếu tồn tại một vectơ $0 \ne u \in K^n$ sao cho: $Au = {\lambda}u$

Khi đó vectơ u được gọi là vectơ riêng (VTR) của ma trận A ứng với giá trị riêng $\lambda$

1.2 Tính chất:

1. Giá trị riêng $\lambda$ chính là nghiệm của phương trình $latex det(A-{\lambda}I) = 0 &fg=ff0000$ (1) được gọi là phương trình đặc trưng của ma trận A.

2. Một giá trị riêng có thể có nhiều vectơ riêng.

3. Mỗi vectơ riêng chỉ ứng với một giá trị riêng duy nhất.

4. Ma trận A là nghiệm của đa thức đặc trưng của chính nó (trong trường hợp này đa thức đặc trưng được coi là đa thức ma trận, nghĩa là biến số của nó không phải là biến số thực mà là biến ma trận)

5. Nếu ${\lambda} = 0$ là giá trị riêng của ma trận A thì A không khả nghịch. Ngược lại, nếu mọi GTR của A đều khác không thì A khả nghịch.

6. Nếu ${\lambda}$ là GTR của ma trận A thì ${\lambda}^k$ là giá trị riêng của ma trận $A^k$

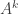
Chứng minh:

1. Số $\lambda$ là trị riêng của A khi và chỉ khi $Au = {\lambda}u (u \ne 0)$ . Suy ra: hệ phương trình tuyến tính thuần nhất $(A-{\lambda}I)u = 0$ có nghiệm $u{\ne}0 \Leftrightarrow det(A-{\lambda}I) = 0$ .

2. Điều này là hiển nhiên vì dựa vào định nghĩa và tính chất 1 thì hệ phương trình $(A-{\lambda}I)u = 0$ có vô số nghiệm.

3. Giả sử vectơ riêng $u_1$ ứng với 2 trị riêng ${\lambda}_1 ; {\lambda}_2$ .

Ta cần chứng minh: ${\lambda}_1 = {\lambda}_2$ . Thật vậy, ta có :

$Au_1 = {\lambda}_1u_1 ; Au_1 = {\lambda}_2u_1 \Rightarrow {\lambda}_1u_1 - {\lambda}_2u_1 = 0 \Rightarrow ({\lambda}_1 - {\lambda}_2)u_1 = 0$

Mà: $u_1 \ne 0$ . Do đó: ${\lambda}_1 - {\lambda}_2 = 0$ ◊

4. Ta có:

$P({\lambda}) = det(A -{\lambda}I) \Rightarrow P(A) = det(A - A.I) = det(A-A) = 0$

5. Do ${\lambda} = 0$ là GTR của ma trận A. Do đó:

$P(0) = det(A-0.I) = 0 \Rightarrow det(A) = 0$ .

Chứng tỏ A suy biến (không khả nghịch).

6. Ta có $Au = {\lambda}u$ . Do đó:

$A^2u = (A.A).u = A.(A.u) = A.({\lambda}u) = {\lambda}.Au = {\lambda}^2u$ .

Từ đó, bằng cách chứng minh quy nạp, bạn sẽ có kết quả.

Nhận xét: từ kết quả trên, ta nhận thấy có 1 cách để tính nhanh $|A-aI|$ . Đó là ta tìm đa thức đặc trưng $P({\lambda}) = |A-{\lambda}I|$ của ma trận A. Sau đó, tính giá trị của P(a).

1.3. Phương pháp giải tìm trị riêng, vectơ riêng:

Bước 1: Giải phương trình đặc trựng $det(A-{\lambda}I) = 0 (1)$ tìm giá trị riêng.

Bước 2: Tìm vectơ riêng ứng với giá trị riêng $\lambda$ :

Ứng với mỗi giá trị riêng ${\lambda}_i$ vừa tìm được, ta giải hệ phương trình tuyến tính thuần nhất $(A-{\lambda}_iI)u = 0 (2)$

Lưu ý: theo tính chất trên, thì hpt (2) luôn luôn có vô số nghiệm. Do đó, nếu bạn giải pt (2) mà vô nghiệm hoặc có nghiệm duy nhất thì phải kiểm tra lại.

1.4 Không gian con riêng ứng với GTR ${\lambda}$

Các vetơ riêng của ma trận A ứng với giá trị riêng ${\lambda}_0$ cùng với vectơ 0 tạo thành 1 không gian con được gọi là không gian con riêng ứng với ${\lambda}_0$ .

Ký hiệu: $E({\lambda}_0) = \left\{u \in K^n : Au ={\lambda}u\right\}$

Nếu giá trị riêng ${\lambda}_0$ là nghiệm bội k thì $dimE({\lambda}_0) \le k$

1.5 Các ví dụ :

Ví dụ 1. Tìm GTR, VTR của ma trận A: $\left[\begin{array}{rr} -1 & 3 \\ -2 & 4 \\ \end{array} \right]$

Bước 1: Lập phương trình đặc trưng của ma trận A:

$P({\lambda}) = det(A-{\lambda}I) = 0 \Leftrightarrow \left|\begin{array}{rr} -1-{\lambda} & 3 \\ -2 & 4-{\lambda} \\ \end{array} \right| = 0 \Leftrightarrow {\lambda}^2 - 3{\lambda} + 2 = 0$

Giải phương trình đặc trưng, ta có: ${\lambda}_1 = 1; {\lambda}_2 = 2$

Bước 2: Tìm các VTR:

1. Ta tìm các VTR ứng với giá trị riêng ${\lambda}_1 = 1$

Ứng với giá trị riêng ${\lambda}_1 = 1$ ta có VTR $u_1 = (x;y)$ là nghiệm của hệ phương trình:

$(A-I)u_1 = 0 \Leftrightarrow \left\{\begin{array}{c} -2x+3y = 0 \\ -2x+3y = 0 \\ \end{array} \right. \Rightarrow 2x = 3y$

Vậy VTR ứng với GTR ${\lambda}_1 = 1$ có dạng $u_1 = (3a;2a) = (3;2)a ; a \ne 0$

2. Ta tìm các VTR ứng với giá trị riêng ${\lambda}_2 = 2$

Ứng với giá trị riêng ${\lambda}_2 = 2$ ta có VTR $u_2 = (x;y)$ là nghiệm của hệ phương trình:

$(A-I)u_2 = 0 \Leftrightarrow \left\{\begin{array}{c} -3x+3y = 0 \\ -2x+2y = 0 \\ \end{array} \right. \Rightarrow x = y$

Vậy VTR ứng với GTR ${\lambda}_2 = 2$ có dạng $u_2 = (b;b) = (1;1)b ; b \ne 0$

Ví dụ 2: Tìm GTR, VTR của ma trận A: $\left[\begin{array}{rr} 1 & 2 \\ -2 & 1 \\ \end{array} \right]$ , xem A là ma trận phức

Bước 1: Lập phương trình đặc trưng của ma trận A:

$det(A-{\lambda}I) = 0 \Leftrightarrow \left|\begin{array}{rr} 1-{\lambda} & 2 \\ 2 & 1-{\lambda} \\ \end{array} \right| = 0 \Leftrightarrow (1-{\lambda})^2 + 4 = 0 (1)$

Phương trình (1) vô nghiệm thực. Tuy nhiên do A là ma trận phức nên ta tìm GTR phức của ma trận. Giải phương trình đặc trưng, ta có: ${\lambda}_1 = 1+2i; {\lambda}_2 = 1-2i$

Bước 2: Tìm các VTR:

1. Ta tìm các VTR ứng với giá trị riêng ${\lambda}_1 = 1+2i$

Ứng với giá trị riêng ${\lambda}_1 = 1+2i$ ta có VTR $u_1 = (x;y) ; x, y \in C$ là nghiệm của hệ phương trình:

$(A-(1+2i)I)u_1 = 0 \Leftrightarrow \left\{\begin{array}{c} -2ix+2y = 0 \\ -2x-2iy = 0 \\ \end{array} \right. \Rightarrow y = ix$

Vậy VTR ứng với GTR ${\lambda}_1 = 1+2i$ có dạng $u_1 = (a;ia) = (1;i)a ; a \ne 0$

2. Ta tìm các VTR ứng với giá trị riêng ${\lambda}_2 = 1-2i$

Ứng với giá trị riêng ${\lambda}_2 = 1-2i$ ta có VTR $u_2 = (x;y) ; x, y \in C$ là nghiệm của hệ phương trình:

$(A-(1-2i)I)u_2 = 0 \Leftrightarrow \left\{\begin{array}{c} 2ix+2y = 0 \\ -2x+2iy = 0 \\ \end{array} \right. \Rightarrow x = iy$

Vậy VTR ứng với GTR ${\lambda}_1 = 1-2i$ có dạng $u_2 = (ia;a) = (i;1)a ; a \ne 0$

Ví dụ 3:

a. Tìm đa thức đặc trưng của ma trận: $A = \left[\begin{array}{rrr} 1 & -1 & -1 \\ 1 & 3 & 1 \\ -3 & 1 & -1 \\ \end{array} \right]$

b. Dựa vào đa thức đặc trưng, chứng minh A khả nghịch và chỉ ra biểu thức xác định $A^{-1}$

c. Tính $det(A-2008I_3)$

d. Tìm GTR, VTR của A.

Giải.

a. Tương tự như các ví dụ trên, ta dễ dàng tìm được đa thức đặc trưng của ma trận A:

$P({\lambda}) = {\lambda}^3 -3{\lambda}^2-4{\lambda}+12$

b. Theo tính chất 4 ta có: $P(A) = A^3-3A^2-4A+12I_3 = 0$ . Do đó:

$-A^3+3A^2+4A=12I_3 \Rightarrow A(-A^2+3A+4I_3)=(-A^2+3A+4I_3).A=12I_3$

Đặt $B = { \dfrac{1}{12}}(-A^2+3A+4I_3)$ .

Ta có: $A.B = B.A = I_3$ .

Do đó: A khả nghịch và $A^{-1} = -A^2+3A+4I_3$

c. Ta có $P({\lambda}) = det(A-{\lambda}I_3)$ nên:

$det(A-2008I_3) = P(2008) = 2006.2010.2005$

d. Từ đa thức đặc trưng ta tìm được các GTR: ${\lambda}_1=-2 ; {\lambda}_2=2 ; {\lambda}_3 = 3$

Khi đó: VTR ứng với giá trị riêng ${\lambda}_1 = -2$ có dạng: $u_1 = (1;-1;4)a , a \ne 0$

VTR ứng với giá trị riêng ${\lambda}_1 = 2$ có dạng: $u_2 = (-1;0;1)b , b \ne 0$

VTR ứng với giá trị riêng ${\lambda}_1 = 3$ có dạng: $u_3 = (-1;1;1)c , c \ne 0$

Đánh giá:

Chia sẻ:

In
PDF
Email
Facebook

Thích Đang tải...

Trang: 1 2

Thảo luận

37 bình luận về “Trị riêng, vectơ riêng của ma trận (Eigenvalues and Eigenvectors)”

Chỉ dùm bài tập:Cho ma trận thực A cấp 2 X1,X2 là hai vecto cột ĐLTT.Biết A.X1=X2,A.X2=X1.Tìm tất cả trị riêng và vecto riêng của A^100

ThíchThích
Posted by Thanh | 02/02/2015, 22:09 Reply to this comment
- Em có: $A.X_1 = X_2$ . Suy ra: $A.(A.X_1) = A.X_2$ . Hay: $A^2.X_1 = A.X_2 = X_1$ . Bằng cách quy nạp em sẽ có: $A^{100}.X_1 = X_1 = I_2.X_1$ Vậy $A^{100} = I_2$ . Từ đó dễ dàng tìm trị riêng và ve1cto riêng.
  
  ThíchThích
  Posted by 2Bo02B | 09/03/2015, 11:15 Reply to this comment