Trong Mặt Phẳng Tọa độ Oxy, Cho Hai đường Tròn . Bài 20 Trang 199 ...

Trong mặt phẳng tọa độ Oxy, cho hai đường tròn: (C1) : \({x^2} + {y^2} + 10x = 4\) và (C2) :  \({x^2} + {y^2} - 4x - 2y - 20 = 0\) có tâm lần lượt là I, J.

a) Viết phương trình đường tròn (C)  đi qua giao điểm của (C1) , (C2)  và có tâm nằm trên đường thẳng d: x - 6y + 6 = 0.

b) Viết phương trình tiếp tuyến chung của (C1) và (C2). Gọi \({T_1},{T_2}\) lần lượt là tiếp điểm của (C1) , (C2) với một tiếp tuyến chung, hãy viết phương trình đường thẳng \(\Delta \) qua trung điểm của \({T_1},{T_2}\) và vuông góc với IJ.

Gợi ý làm bài

(Xem hình 3.43)

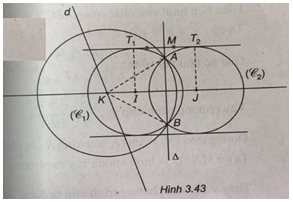
a) (C1) có tâm I(-5 ; 0), bán kính \({R_1} = 5\). (C2) có tâm I(2 ; 1), bán kính \({R_2} = 5\)

Tọa độ của giao điểm A, B của (C1) và (C2) là nghiệm của hệ phương trình:

\(\eqalign{ & \left\{ \matrix{ {x^2} + {y^2} + 10x = 0 \hfill \cr {x^2} + {y^2} - 4x - 2y - 20 = 0 \hfill \cr} \right. \cr & \Leftrightarrow \left\{ \matrix{ 14x + 2y + 20 = 0 \hfill \cr {x^2} + {y^2} + 10x = 0 \hfill \cr} \right. \cr} \)

Ta được A(-1 ; -3), B(-2 ; 4).

Gọi K là tâm của (C) ta có \(KA = KB = R \Rightarrow K \in IJ.\)

Phương trình IJ là : x - 7y + 5 = 0.

Tọa độ K là nghiệm của hệ phương trình:

Advertisements (Quảng cáo)

\(\left\{ \matrix{ x - 7y + 5 = 0 \hfill \cr x - 6y + 6 = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ x = - 12 \hfill \cr y = - 1 \hfill \cr} \right.\)

Vậy K(-12 ; -1). Ta có \({R^2} = K{A^2} = 125.\)

Vậy phương trình của đường tròn (C) là : \({\left( {x + 12} \right)^2} + {\left( {y + 1} \right)^2} = 125.\)

b) \({R_1} = {R_2} = 5\)

=> tiếp tuyến chung \(l\) của (C1) và (C2) song song với IJ. Phương trình \(l\) có dạng : 

x - 7y + c = 0.

Ta có: \(d(I,l) = {R_1}\)

\(\eqalign{ & \Leftrightarrow {{\left| { - 5 + c} \right|} \over {\sqrt {1 + 49} }} = 5 \cr & \Leftrightarrow \left| {c - 5} \right| = 25\sqrt 2 \cr & \Leftrightarrow c = 5 \pm 25\sqrt 2 . \cr} \)

Vậy phương trình của hai tiếp tuyến chung của (C1) và (C2) là : 

\(x - 7y + 5 \pm 25\sqrt 2  = 0.\)

Đường thẳng AB đi qua trung điểm M của \({T_1}{T_2}\) và vuông góc với IJ.

Phương trình của AB là : 7x + y + 10 = 0.