" Trong Một đường Tròn, đường Kính Vuông Góc Với Một Dây Thì đi ...
Có thể bạn quan tâm
HOC24
Lớp học Học bài Hỏi bài Giải bài tập Đề thi ĐGNL Tin tức Cuộc thi vui Khen thưởng- Tìm kiếm câu trả lời Tìm kiếm câu trả lời cho câu hỏi của bạn
Lớp học
- Lớp 12
- Lớp 11
- Lớp 10
- Lớp 9
- Lớp 8
- Lớp 7
- Lớp 6
- Lớp 5
- Lớp 4
- Lớp 3
- Lớp 2
- Lớp 1
Môn học
- Toán
- Vật lý
- Hóa học
- Sinh học
- Ngữ văn
- Tiếng anh
- Lịch sử
- Địa lý
- Tin học
- Công nghệ
- Giáo dục công dân
- Tiếng anh thí điểm
- Đạo đức
- Tự nhiên và xã hội
- Khoa học
- Lịch sử và Địa lý
- Tiếng việt
- Khoa học tự nhiên
- Hoạt động trải nghiệm
- Hoạt động trải nghiệm, hướng nghiệp
- Giáo dục kinh tế và pháp luật
Chủ đề / Chương
Bài học
HOC24
Khách vãng lai Đăng nhập Đăng ký Khám phá Hỏi đáp Đề thi Tin tức Cuộc thi vui Khen thưởng - Tất cả
- Toán
- Vật lý
- Hóa học
- Sinh học
- Ngữ văn
- Tiếng anh
- Lịch sử
- Địa lý
- Tin học
- Công nghệ
- Giáo dục công dân
- Tiếng anh thí điểm
- Hoạt động trải nghiệm, hướng nghiệp
- Giáo dục kinh tế và pháp luật
Câu hỏi
Hủy Xác nhận phù hợp Chọn lớp Tất cả Lớp 12 Lớp 11 Lớp 10 Lớp 9 Lớp 8 Lớp 7 Lớp 6 Lớp 5 Lớp 4 Lớp 3 Lớp 2 Lớp 1 Môn học Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Tiếng anh thí điểm Đạo đức Tự nhiên và xã hội Khoa học Lịch sử và Địa lý Tiếng việt Khoa học tự nhiên Hoạt động trải nghiệm Hoạt động trải nghiệm, hướng nghiệp Giáo dục kinh tế và pháp luật Mới nhất Mới nhất Chưa trả lời Câu hỏi hay
- Nguyễn SSS
1) Chứng minh định lý: " Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy."
2) Chứng minh định lý: " Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy."
Xem chi tiết Lớp 9 Toán Câu hỏi của OLM 0 0
Gửi Hủy 
- Nguyên Anh Phạm
1.Khoanh tròn vào mệnh đề sai:A. Trong một đường tròn, đường kính đi qua trung điểm của một dây cung thì chia cung căng dây ấy thành 2 phần bằng nhau.B. Trong một đường tròn, đường kính đi qua điểm chính giữa của một cung thì vuông góc với dây căng cung ấy và ngược lại.C. Trong một đường tròn, đường kính đi qua điểm chính giữa của một cung thì đi qua trung điểm của dây căng cung ấy.D. Trong một đường tròn, hai cung bị chắn bởi hai dây song song thì bằng nhau.
2.Khoanh tròn vào khẳng định đúng:A. Tứ giác có tổng hai góc bằng 1800 thì tú giác đó nội tiếp.B. Tứ giác có bốn đỉnh cách đều 1 điểm O cho trước thì nội tiếp.C. Tứ giác có hai đỉnh cùng nhìn cạnh chứa 2 đỉnh còn lại dưới một góc a thì nội tiếp.D. Tứ giác có hai đỉnh cùng nhìn cạnh còn lại dưới một góc vuông thì nội tiếp.E. Tứ giác có 1 góc bằng góc ngoài của góc đối diện thì nội tiếp.
Xem chi tiết Lớp 9 Toán Bài 3: Giải hệ phương trình bằng phương pháp thế 1 0 Gửi Hủy 
Nguyễn Lê Phước Thịnh CTV 
26 tháng 7 2023 lúc 20:11 2: B,E
Đúng 0 Bình luận (0) Gửi Hủy 
- Pham Trong Bach
a) Chứng minh rằng đường kính đi qua điểm chính giữa của một cung thì đi qua trung điểm của dây cung căng cung ấy. Mệnh đề đảo có đúng không? Hãy nêu thêm điều kiện để mệnh đề đảo đúng.
b) Chứng minh rằng đường kính đi qua điểm chính giữa của một cung thì vuông góc với dây cung ấy và ngược lại.
Xem chi tiết Lớp 9 Toán 1 0 Gửi Hủy 
Cao Minh Tâm 
24 tháng 8 2017 lúc 6:03 a)
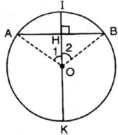
Vẽ đường tròn tâm O, dây cung AB.
Gọi I là điểm chính giữa của cung AB.
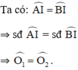
Gọi OI ∩ AB = H.
ΔAOH và ΔBOH có: AO = OB, O 1 ^ = O 2 ^ ; OH chung
⇒ ΔAOH = ΔBOH (c-g-c)
⇒ AH = BH (hai cạnh tương ứng)
⇒ OI đi qua trung điểm H của AB.
+ Mệnh đề đảo: Đường kính đi qua trung điểm của một dây cung thì đi qua điểm chính giữa của cung đó.
Mệnh đề sai
Ví dụ: Chọn dây cung AB là một đường kính của (O) (AB đi qua O). Khi đó, tồn tại đường kính CD đi qua O là trung điểm của AB nhưng C,D không phải là điểm chính giữa cung AB ( hình vẽ)
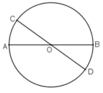
Mệnh đề đảo chỉ đúng khi dây cung AB không phải đường kính.
b)
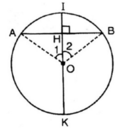
+ Cho đường tròn (O); dây cung AB ;
I là điểm chính giữa cung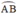 
, H = OI ∩ AB.
⇒ ΔAOH = ΔBOH (cm phần a).
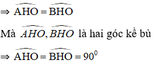
⇒ OH ⊥ AB.
Vậy đường kính đi qua điểm chính giữa của cung thì vuông góc với dây căng cung ấy.
+ Cho đường tròn (O); dây cung AB.
Kẻ đường thẳng OH ⊥ AB (H ∈ AB) cắt đường tròn tại I.
Ta có: ΔABO cân tại O (vì AO = OB = R).
⇒ đường cao OH đồng thời là đường phân giác
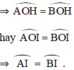
⇒ I là điểm chính giữa của cung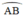 
Vậy đường kính vuông góc với dây căng cung thì đi qua điểm chính giữa của cung.
Kiến thức áp dụng
+ Điểm chính giữa cung là điểm chia cung thành hai cung bằng nhau.
Đúng 1 Bình luận (0) Gửi Hủy - Pham Trong Bach
“Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì…với dây ấy”. Điền vào dấu…cụm từ thích hợp
A. nhỏ hơn
B. bằng
C. song song
D. vuông góc
Xem chi tiết Lớp 9 Toán 1 0 Gửi Hủy Cao Minh Tâm 5 tháng 1 2019 lúc 7:32 Đáp án D
Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy
Đúng 0 Bình luận (0) Gửi Hủy - Pham Trong Bach
“Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì…với dây ấy”. Điền vào dấu…cụm từ thích hợp
A. nhỏ hơn
B. bằng
C. song song
D. vuông góc
Xem chi tiết Lớp 9 Toán 1 0 Gửi Hủy Cao Minh Tâm 16 tháng 5 2017 lúc 13:20 Chọn đáp án D.
Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy
Đúng 0 Bình luận (0) Gửi Hủy 
- Bài 14
a) Chứng minh rằng đường kính đi qua điểm chính giữa của một cung thì đi qua trung điểm của cung căng dây ấy. Mệnh đề đảo có đúng không? Hãy thêm điều kiện để mệnh đề đảo đúng.
b) Chứng minh rằng đường kính đi qua điểm chính giữa của một cung thì vuông góc với dây căng cung ấy và ngược lại.
Xem chi tiết Lớp 9 Toán Bài 2: Liên hệ giữa cung và dây 1 0 Gửi Hủy 
Quốc Đạt 
11 tháng 4 2017 lúc 11:01 a) Giả sử đường kính CD của đường tròn (O) có C là điểm chính giữa của cung AB, nghĩa là cung AC = cung CB suy ra ∠O1 = ∠O2
Gọi I là giao điểm của CD và AB. Khi đó OI là phân giác, đồng thời là trung tuyến của tam giác OAB (Do ΔOAB cân đỉnh O)
Vậy I là trung điểm của AB.
+ Mệnh đề đảo không đúng vì nếu dây cung AB cũng là một đường kính thì dây CD đi qua trung điểm của dây AB nhưng không đi qua điểm chính giữa của cung AB.
+ Để mệnh đề đảo chúng ta cần bổ sung thêm: Đường kính đi qua trung điểm một dây không đi qua tâm của đường tròn thì đi qua điểm chính giữa của cung bị căng bởi dây ấy.
b) Thuận: Giả sử đường kính CD đi qua C là điểm chính giữa cung AB ⇒ cungAC = cungCB ⇒ AOC = COB ⇒ OC là tia phân giác của góc ∠AOB
Vì ΔOAB cân đỉnh O nên đường phân giác đồng thời là đường cao.
Vậy: OC ⊥ AB hay CD ⊥ AB.
Đảo: Giả sử đường kính AB ⊥ CD tại I.
Khi đó: OI là tia phân giác của góc ∠AOB ⇒ AOC = BOC ⇒ AC= BC
⇒ C là điểm giữa cung AB.
Đúng 0 Bình luận (1) Gửi Hủy - Pham Trong Bach
Hãy đưa ra một ví dụ để chứng tỏ rằng đường kính đi qua trung điểm của một dây có thể không vuông góc với dây ấy.
Xem chi tiết Lớp 9 Toán 1 0 Gửi Hủy Cao Minh Tâm 15 tháng 5 2018 lúc 10:48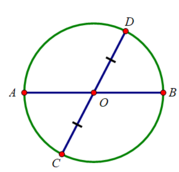 
O là trung điểm của CD
AB đi qua trung điểm của CD nhưng AB không vuông góc với CD
Đúng 0 Bình luận (0) Gửi Hủy - Pham Trong Bach
Hãy đưa ra một ví dụ để chứng tỏ rằng đường kính đi qua trung điểm của một dây có thể không vuông góc với dây ấy.
Xem chi tiết Lớp 9 Toán 1 0 Gửi Hủy Cao Minh Tâm 13 tháng 6 2018 lúc 8:32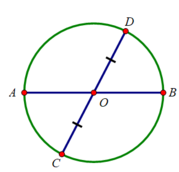 
O là trung điểm của CD
AB đi qua trung điểm của CD nhưng AB không vuông góc với CD
Đúng 0 Bình luận (0) Gửi Hủy - Pham Trong Bach
Chứng minh rằng đường kính đi qua điểm chính giữa của một cung thì vuông góc với dây cung ấy và ngược lại.
Xem chi tiết Lớp 9 Toán 1 0 Gửi Hủy Cao Minh Tâm 6 tháng 9 2017 lúc 6:31 
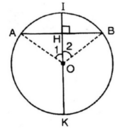
+ Cho đường tròn (O); dây cung AB ;
I là điểm chính giữa cung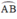 
, H = OI ∩ AB.
⇒ ΔAOH = ΔBOH (cm phần a).
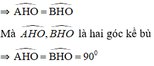
⇒ OH ⊥ AB.
Vậy đường kính đi qua điểm chính giữa của cung thì vuông góc với dây căng cung ấy.
+ Cho đường tròn (O); dây cung AB.
Kẻ đường thẳng OH ⊥ AB (H ∈ AB) cắt đường tròn tại I.
Ta có: ΔABO cân tại O (vì AO = OB = R).
⇒ đường cao OH đồng thời là đường phân giác
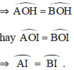
⇒ I là điểm chính giữa của cung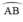 
Vậy đường kính vuông góc với dây căng cung thì đi qua điểm chính giữa của cung.
Kiến thức áp dụng
Đúng 0 Bình luận (0) Gửi Hủy 
- lê thị thu huyền
hãy đưa ra một ví dụ để chứng tỏ rằng đường kính đi qua trung điểm của một dây có thể không vuông góc với dây ấy.
Xem chi tiết Lớp 9 Toán Câu hỏi của OLM 3 0 Gửi Hủy 
ling min laura 24 tháng 10 2017 lúc 20:37 AB vuông góc với CD tại I
suy ra IC = ID
Suy ra " đường kính vuông góc vs dây thì đi qua trung điểm của dây đó "
Cậu cứ the mak làm ngược lại nhà Huyen . Sai thj thông cảm cho tôi nha bà
Đúng 0 Bình luận (0) Gửi Hủy 
Shiba Inu 
24 tháng 10 2017 lúc 20:15 Cậu vào google nhé !
Đúng 0 Bình luận (0) Gửi Hủy 
minhduc 24 tháng 10 2017 lúc 20:24 VD : đường kính đi qua trung điểm của sợi dây có thể ko vuông góc với nó .
A B C D O AB: là đường kính . ; CD: là sợi dây .
Đúng 0 Bình luận (0) Gửi Hủy Từ khóa » Cách Chứng Minh đường Kính Vuông Góc Với Dây Cung
-
Lý Thuyết Về đường Kính Và Dây Của đường Tròn | SGK Toán Lớp 9
-
Cách Chứng Minh Bán Kính Vuông Góc Với Dây Cung
-
Hình Học 9 Bài 2: Đường Kính Và Dây Của đường Tròn
-
Chứng Minh đường Kính Vuông Góc Với Dây Cung
-
Lý Thuyết: Đường Kính Và Dây Của đường Tròn
-
Đường Kính Và Dây Của đường Tròn - Lý Thuyết Toán
-
Lý Thuyết đường Kính Và Dây Của đường Tròn Toán 9
-
Đường Kính Vuông Góc Với Dây Cung
-
Đường Kính Vuông Góc Với Dây Cung
-
Bài 14 A) Chứng Minh Rằng đường Kính đi Qua điểm Chính Giữa Của ...
-
Giải Toán 9 Bài 2. Liên Hệ Giữa Cung Và đây
-
Chứng Minh Rằng đường Kính đi Qua điểm Chính Giữa Của Một Cung ...
-
Quan Hệ Giữa đường Kính Và Dây Của đường Tròn ? Định Lý, Bài Tập