Trực Tâm Là Gì? Định Nghĩa, Tính Chất Và Cách Xác định Trực Tâm Tam ...

Trực tâm trong không gian, trực tâm tam giác là kiến thức mà chúng ta đã được học trong chương trình toán học ở THCS. Tuy nhiên, sau thời gian dài nên nhiều người dùng không còn nhớ rõ trực tâm là gì? Vậy các bạn hãy cùng các chuyên gia tại Trang công nghệ số 1 tại Việt Nam – HPConnect.vn tìm hiểu về định nghĩa, tính chất và cách xác định trực tâm tam giác ngay sau đây nhé!

Nội Dung Chính

• 1 Định nghĩa trực tâm là gì?
• 2 Tính chất trực tâm
• 3 Hướng dẫn cách xác định trực tâm trong tam giác
• 4 Các dạng bài toán về trực tâm của tam giác từ cơ bản đến nâng cao
  • 4.1 Ví dụ 1
  • 4.2 Ví dụ 2
  • 4.3 Ví dụ 3
• 5 Kết luận

Định nghĩa trực tâm là gì?

Trực tâm là gì? Trực tâm tam giác là gì? Trong một tam giác, 3 đường cao cùng giao nhau tại một điểm. Điểm này được gọi là trực tâm của tam giác đó. Hoặc chúng ta có thể phát biểu rằng trực tâm của tam giác là giao điểm của 3 đường cao.

Đường cao của tam giác là gì? Các bạn có thể hiểu đường cao của tam giác là một đoạn thẳng được kẻ từ một đỉnh sao cho vuông góc với cạnh đối diện. Trong mỗi tam giác sẽ có 3 đường cao tương ứng với 3 cạnh đối diện và 3 đỉnh.

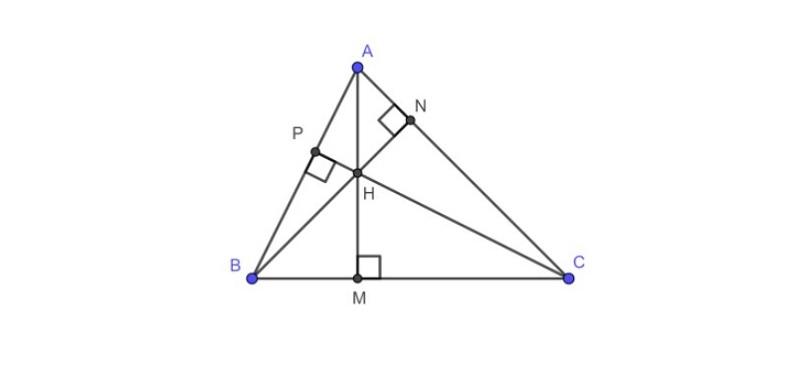
Ví dụ: Cho hình tam giác ABC có 3 đường cao lần lượt là AM, BN, CP. Gọi H là giao điểm của 3 đường cao trong tam giác. Như vậy, H chính là trực tâm của tam giác ABC.

Tính chất trực tâm

Tính chất trực tâm trong tam giác được đánh giá là tài liệu vô cùng hữu ích. Hôm nay, các chuyên gia tại Trang công nghệ số 1 tại Việt Nam – HPConnect.vn xin giới thiệu đến các bạn như sau:

+ Tính chất 1: Trong một tam giác cân, đường trung trực tương ứng với cạnh đáy cũng chính là đường cao, đường phân giác và đường trung tuyến của tam giác đó.

+ Tính chất 2: Trong một tam giác, nếu có một đường trung tuyến cũng là đường trung trực của tam giác. Suy ra, hình tam giác này là tam giác cân.

+ Tính chất 3: Trong một tam giác, nếu có một đường trung tuyến cũng chính là đường trung trực. Suy ra, hình tam giác đó là tam giác cân.

+ Tính chất 4: Trực tâm của tam giác nhọn ABC trùng với tâm đường tròn nội tiếp tam giác trong trường hợp có 3 đỉnh là chân của 3 đường cao được nối từ đỉnh A, B, C đến những cạnh đối diện tương ứng AB, AC, BC.

+ Tính chất 5: Nếu đường cao của tam giác tương ứng với một đỉnh cắt đường tròn ngoại tiếp ở điểm thứ 2. Như vậy, sẽ đối xứng với trực tâm qua cạnh tương ứng.

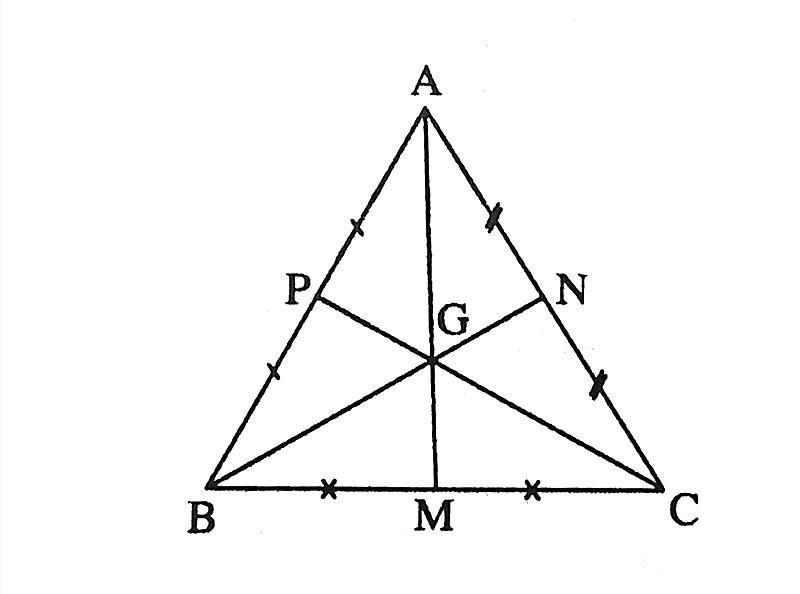
– Từ các tính chất của trực tâm tam giác ở trên, chúng ta có thể rút ra được hệ quả như sau:

Trong một hình tam giác đều, trọng tâm, trực tâm, điểm thuộc tam giác, điểm cách đều 3 cạnh, cách đều 3 đỉnh. 4 điểm này sẽ trùng nhau và nó chính là 1 điểm.

Hướng dẫn cách xác định trực tâm trong tam giác

Đối với mỗi hình tam giác, sẽ có vị trí cũng như cách xác định trực tâm tương ứng. Để biết được cách xác định trực tâm trong tam giác. Mời các bạn tiếp tục theo dõi những thông tin chia sẻ sau đây nhé!

Video giải thích trực tâm là gì? Cách xác định trực tâm tam giác

Trực tâm của tam giác chính là giao điểm của 3 đường cao trong tam giác đó.

Tuy nhiên, các bạn không nhất thiết phải vẽ 3 đường cao khi muốn xác định trực tâm trong tam giác. Vì chỉ cần vẽ 2 đường cao của tam giác thì bạn đã biết được trực tâm của tam giác đó.

Đối với những loại tam giác thông thường như tam giác đều, tam giác cân hoặc tam giác nhọn. Cách xác định trực tâm của những loại này sẽ giống nhau. Từ hai đỉnh bất kỳ của tam giác, bạn kẻ 2 đường cao đến 2 cạnh đối diện. Trực tâm của tam giác chính là điểm giao nhau của 2 đường cao này. Và tất nhiên là đường cao còn lại cũng đi qua trực tâm của hình tam giác.

Đối với tam giác vuông, quá trình xác định đường cao sẽ có sự khác biệt. Khi tam giác vuông sẽ có 2 đường cao chính là 2 cạnh góc vuông của tam giác đó. Vì 2 cạnh này vuông góc với nhau. Do đó, trực tâm của tam giác vuông chính là đỉnh của góc vuông trong tam giác.

>>> Xem thêm:

• Công thức tính chu vi hình Vuông và các dạng bài tập liên quan
• Định nghĩa về tam giác đều, tính chất và diện tích tam giác đều
• Tam giác vuông là gì? Cách tính diện tích tam giác vuông chuẩn xác

Các dạng bài toán về trực tâm của tam giác từ cơ bản đến nâng cao

Sau khi đã tìm hiểu rõ về khái niệm trực tâm là gì, các tính chất, cách xác định trực tâm trong tam giác,… Các bạn hãy cùng các chuyên gia tại HPConnect.vn giải một số bài tập để củng cố lại kiến thức và ghi nhớ lâu hơn nhé!

Ví dụ 1

Cho tam giác ABC cân tại A, tam giác có đường trung tuyến AM cùng với đường cao BK. Gọi H chính là giao điểm của trung tuyến AM và đường cao BK. Hãy chứng minh rằng CH vuông góc với AB?

Hướng dẫn giải:

Theo giả thuyết, tam giác ABC cân tại A. Vì vậy, đường trung tuyến AM cũng chính là đường cao của tam giác cân ABC.

Ta có, H là giao điểm của đường cao BK và đường cao AM. Suy ra, H là trực tâm của tam giác cân ABC.

Từ đó, CH cũng là đường cao của tam giác cân ABC.

Vậy CH sẽ vuông góc với cạnh AB.

Ví dụ 2

Cho hình vẽ như hình bên dưới:

1. a) Hãy chứng minh rằng NS vuông góc với LM?
2. b) Cho góc LNP = 50 độ. Yêu cầu tính góc MSP và góc PSQ?

Hướng dẫn giải:

1. a) Trong tam giác MNL có:

LP vuông góc với MN => LP chính là đường cao của tam giác MNL.

MQ vuông góc với NL => MQ chính là đường cao của tam giác MNL.

Mặc khác, LP và MQ cắt nhau tại điểm S.

Theo tính chất ba đường cao trong một tam giác, ta suy ra S chính là trực tâm của tam giác MNL.

=> Đường thẳng SN cũng là đường cao của tam giác MNL.

Vậy SN vuông góc với LM.

1. b) Tam giác NMQ vuông tại Q có:

^LNP + ^QMN = 90 => ^LNP = 90 – ^QMN

Tam giác MPS vuông tại P có:

^QMN + ^MSP = 90 => ^MSP = 90 – ^QMP

=> ^LNP = ^MSP

Mà ^LNP = 50 (theo giả thuyết).

Từ đó, ta suy ra ^MSP = 50

Với ^MSP + ^PSQ = 180 => ^PSQ = 180 – ^MSP = 180 – 50 = 130

Vậy ^MSP = 50, ^PSQ = 130.

Ví dụ 3

Cho hình tam giác nhọn ABC có trực tâm là H. Hãy chứng minh rằng 9 điểm, gồm có 3 đường cao, trung điểm của các đoạn HA, HB, HC và trung điểm 3 cạnh cùng thuộc trên một đường tròn?

Hướng dẫn giải:

Gọi I, L, K lần lượt là chân 3 đường cao được hạ từ 3 đỉnh A, B, C. H là giao điểm của 3 đường cao tam giác ABC.

D, E, F lần lượt là trung điểm của 3 cạnh AB, BC, AC.

G, I, J lần lượt là trung điểm của AH, BH, CH.

Ta có:

DF là đường trung bình của tam giác ABC => DF song song với BC, DF = 1/2BC (1)

IJ là đường trung bình của tam giác HBC => IJ song song với BC, IJ = 1/2BC (2)

Từ (1) & (2), ta suy ra tứ giác DFJI là hình bình hành (3)

Ta có, DI là đường trung bình của tam giác AHB => DI song song với AH nên DI sẽ song song với AI.

Mặc khác, ta lại có AI vuông góc với BC và IJ song song với BC.

=> DI vuông góc với IJ (4)

Từ (3) & (4), ta có tứ giác DFJI là hình chữ nhật. Với tâm đường tròn ngoại tiếp DFJI là O và O chính là trung điểm DJ (a)

Tương tự, chứng minh tứ giác GDEJ là hình chữ nhật. Với tâm đường tròn ngoại tiếp GDEJ là O và O chính là trung điểm DJ (b)

Tam giác GIE vuông tại I. Suy ra, tâm đường tròn ngoại tiếp tam giác GIE là O và trung điểm là GE. Tương tự, O cũng chính là tâm đường tròn ngoại tiếp tam giac JID và tam giác IKE (c)

Từ (a), (b), (c) ta sẽ kết luận rằng 9 điểm là chân đường cao, trung điểm của các đoạn HA, HB, HC và trung điểm 3 cạnh cùng thuộc trên một đường tròn O. 

Kết luận

Như vậy là HPConnect đã chia sẻ đến các bạn những thông tin chi tiết liên quan đến trực tâm. Hy vọng những kiến thức này đã giúp bạn hiểu được Trực tâm là gì? Định nghĩa, tính chất và cách xác định trực tâm tam giác. Chúc các bạn vận dụng vào quá trình giải bài tập hiệu quả và cho kết quả chính xác nhé!