Trung Bình Mẫu – Phương Sai Mẫu - TaiLieu.VN

Có thể bạn quan tâm

Mạng xã hội chia sẻ tài liệu Upload Đăng nhập Nâng cấp VIP Trang chủ » Tài Liệu Phổ Thông » Bài tập cơ bản và nâng cao13 trang 5319 lượt xem 770 Trung bình mẫu – Phương sai mẫu

Tham khảo tài liệu 'trung bình mẫu – phương sai mẫu', tài liệu phổ thông, toán học phục vụ nhu cầu học tập, nghiên cứu và làm việc hiệu quả

yeuthuongSaveLikeShareReport Download AI tóm tắt /13

CHƯƠNG 1:ÔN TẬP 1.1. Trung bình mẫu – Phương sai mẫu 1.1.1.Trung bình mẫu Trong phân tích dữ liệu, cũng như trong cuộc sống hàng ngày, chúng ta thường nói đến chiều cao trung bình, thu nhập trung bình, vân vân. Đó chính là trung bình mẫu. Hãy xét ví dụ sau: Ví dụ 1.1: Bảng quan sát nhiệt độ ở Đà Lạt Thứ 2 Thứ 3 Thứ 4 Thứ 5 (x ()ox5.191820211941=+++=⇒ Một cách khái quát, trung bình mẫuđược tính bằng công thức sau: ()NxxxxNx++++=......1321Hay: ∑==NnnxNx11 1.1.2.Phương sai mẫu Phương sai mẫu [ký hiệu ] bằng trung bình của tổng bình phương độ lệch giữa giá trị quan sát so với giá trị trung bình: 2Xs ()()()⎥⎦⎤⎢⎣⎡++−−−=xxxxxxNsNX222122......1Hay:()∑=−=NnnXxxNs1221 Chẳng hạn, về trung bình mà nói thì khí hậu ở sa mạc rất nóng. Hơn nữa nhiệt độgiao động rất lớn giữa ngày và đêm. Để thể hiện được sự khắc nghiệt của khí hậu sa mạc, chúng ta không những chỉ sử dụng trung bình (mẫu) về nhiệt độ, mà cả sự giao 1) (x2) (x3) (x4) 19o21o20o18o 1

động của nhiệt độ theo từng thời điểm so với trung bình. Đó chính là khái niệm vềphương sai mẫu nói trên. 1.2. Hàm mật độ xác suất, hàm phân bố xác suất 1.2.1.Tần suất và xác suất Để có sự hình dung về tần suất, hãy xét ví dụ sau: Ví dụ 1.2: Xếp hạng tốc độ gia tăng giá cổ phiếu trên thị trường chứng khoán Việt Nam. Gọi X là tỉ lệ phần trăm mức tăng giá cổ phiếu trung bình trong 3 tháng đầu tiên sau khi “lên sàn”; gọi P là phần trăm các công ty có mức tăng giá cổ phiếu tương ứng với giá trị của X X Y (x1) 50% 10% (x2) 40% 20% (x3) 30% 35% (x4) 20% 25% Con số P= 10%, X= 50% có nghĩa là có 10% trong tổng số các công ty có mức tăng giá trong 3 tháng đầu sau khi phát hành cổ phiếu ra công chúng là 50%. Đó chính là ví dụ về tần suất Ví dụ 1.3: Trò chơi tung đồng xu. Giả sử bạn tham gia cuộc chơi tung đồng xu tại hội chợ. Nếu là mặt sấp, bạn sẽđược $100. Ngược lại, nếu là mặt ngửa, bạn được $0. Với thể lệđó, bạn sẵn sàng trả bao nhiêu đôla để tham gia trò chơi? Để cho tiện, hãy kí hiệu mặt sấp là 1, mặt ngửa là 0. Giả sử kết quả tung xu sau 10 lần là như sau: X P 1 3/10 0 7/10 Con số 3/10 chính là tần suất xuất hiện mặt sấp (X = 1). Nghĩa là, trong 10 lần tung xu, có 3 lần xuất hiện mặt sấp. Và do đó, có 7 lần xuất hiện mặt ngửa. Số tiền bạn bỏ ra cho việc tham dự 10 lần tung xu là: $50 x 10 = $500. Số tiền nhận được trong cuộc chơi: $100 x 3 + $0 x 7 = $300. 2

Æ Do vậy, cuộc chơi không hứng thú đối với bạn ($500 > $300). Tuy nhiên, nếu giả sử rằng bạn tham dự cuộc chơi vô hạn lần. Khi đó, số lần xuất hiện mặt sấp và mặt ngửa là như nhau, và bằng ½. Khi đó, kỳ vọng đượccuộc sẽ là: $100x1/2 + $0x1/2 = $50; và bằng chính số tiền lớn nhất bạn sẵn sàng trả để tham dựcuộc chơi. Điều chúng ta cần phân biệt là con số P = 3/10 trong ví dụ nêu trên là tần suất xuất hiện mặt sấp trong 10 lần thử. Và con số ½ là xác suất xuất hiện mặt sấp (hoặc ngửa). Khái niệm tần suất ứng với từng mẫu thử; còn xác suất tương ứng với tổng thể. 1.2.2.Biến ngẫu nhiên rời rạc và liên tục 2.2.1.Biến ngẫu nhiên rời rạc: Một biến ngẫu nhiên là rời rạc nếu các giá trị có thể có của nó lập nên một tập hợp hữu hạn hoặc đếm được, nghĩa là có thể liệt kê được tất cả các giá trị có thể có của nó. Cuộc chơi tung xu nêu trên là ví dụ về biến ngẫu nhiên rời rạc. Một cách hình thức hóa, ta có thể nói như sau. Giả sửđối tượng quan sát X có thểxuất hiện trong K sự kiện khác nhau [trong ví dụ tung xu, K = 2]. Ta ký hiệu các sựkiện đó là . Kxxx,...,,21 Tần suất xuất hiện một biến cố trong N phép thử, ký hiệu là , là tỉ số giữa sốlần xuất hiện biến cố cụ thể đó so với N phép thửđược thực hiện. kxkp Với mọi chỉ số, , ta có thể viết như sau: Kk,...,3,2,1= X x x x … x123K P p p p … p123K p, p12, p,… p3K > 0, và p1 + p2 + p + …… + p3K = 1, hay cũng vậy, 11=∑=Kkkp Nếu số mẫu N là đủ lớn (tiến đến vô hạn), khái niệm tần suất xuất hiện một biến cốđược thay bằng khái niệm xác suất xuất hiện biến cố, ký hiệu bởi: Trong đó, là hàm mật độ xác suất của .,..,2,1),(Kkxffkk==)(kxf....2,1,Kkxk= 3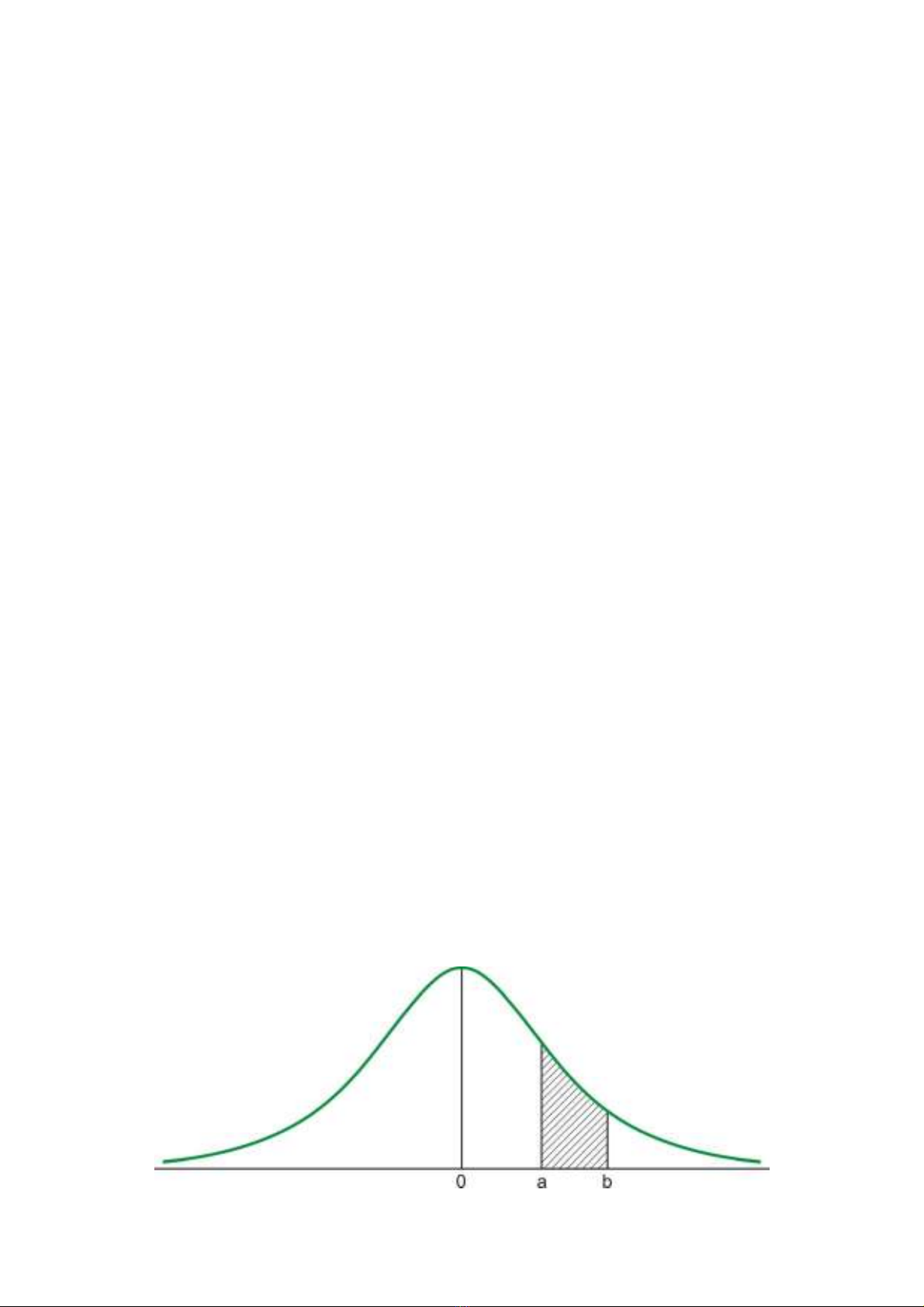

Ta cũng có, f, f, f,… f123K > 0, và 11=∑=Kkkf 2.2.2.Biến ngẫu nhiên liên tục Một biến ngẫu nhiên là liên tục nếu các giá trị có thể có của nó lắp đầy một khỏang trên trục số, nghĩa là không thể liệt kê và đếm được tất cả các giá trị có thể có của nó. Tương tự với trường hợp phân bố xác suất rời rạc, nếu gọi X là một biến ngẫu nhiên liên tục; và f(x) là hàm mật độ xác suất của X. Khi đó: 1)(0)(=≥∫∞+∞−dxxfxf Ta định nghĩa hàm phân bố xác suất của X là: ∫∞−=xdttfxF)()( Điều đó có nghĩa là, xác suất của biến ngẫu nhiên X nhận giá trị trong khoảng sẽ là: ],[ba )()()()(aFbFbXaPbadxxf−==≤≤∫ Ví dụ, trong phân bố chuẩn, về đồ thị ta có thể biểu diễn công thức tính xác suất này như sau: Đồ thị 1.1: Phân bố xác suất 4

Phần tô đậm chính là xác suất)(bXaP≤≤, được tính bởi tích phân: . )()()(aFbFbadxxf−=∫ 1.3. Phân bố xác suất đồng thời Nhiều khi chúng ta muốn đưa ra một đánh giá xác suất đồng thời cho một số biến lượng ngẫu nhiên. Ví dụ, bảng thống kê có ghi lại dữ kiện về thất nghiệp (u) và lạm phát (п). Cả hai biến lượng này đều là biến ngẫu nhiên, rất nhiều khả năng là chính phủ muốn hỏi những nhà kinh tế câu hỏi sau đây: “Liệu khả năng lạm phát thấp hơn 8% và mức độ thất nghiệp nhỏ hơn 6% vào năm saulà bao nhiêu?”. Điều đó có nghĩa là, ta cần phải xác định xác suất đồng thời: P (п < 8, u < 6) = ? Để trả lời được những câu hỏi như vậy, chúng ta cần phải xác định hàm mật độ xác suất đồng thời [joint probability density function]. 1.3.1.Hàm mật độ xác suất đồng thời Định nghĩa: Giả sử X và Y là 2 biến ngẫu nhiên. Hàm mật độ xác suất đồng thời của x và y là: ),(),(yYxXPyxf=== Hàm sốđó cần thỏa mãn điều kiện: 0),(≥yxf, và 1),(=∑∑xyyxf nếu X, Y rời rạc dxdyyxfxy.),(∫∫ nếu X, Y liên tục Khi đó, ∑∑≤≤≤≤=≤≤≤≤bxadycyxfdycbxaP),(),(, nếu X, Y là biến ngẫu nhiên rời rạc, và 5

Tài liêu mới

Phiếu Bài Tập Cuối Tuần 35 - Toán Lớp 2- Cánh Diều

W 8 trang

Tổng hợp bài tập định lý Viète: Tài liệu đầy đủ

Tài liệu Tổng hợp bài tập định lý Viète

W 3 trang

Bài tập ngữ pháp tiếng Anh cơ bản: Ôn luyện hiệu quả

Bài tập ôn luyện ngữ pháp tiếng Anh cơ bản

W 7 trang

Bài tập vận dụng từ vựng, ngữ pháp tiếng Anh (mới nhất)

Bài tập vận dụng về từ vựng, ngữ pháp tiếng Anh

W 11 trang

Bài tập so sánh hơn và so sánh nhất của tính từ [kèm đáp án/mới nhất]

Bài tập So sánh hơn và nhất của tính từ

W 6 trang

Tài liệu tham khảo Tiếng Anh lớp 8

126 trang

Đề ôn tập Vật lý lớp 12: Tổng hợp đề thi, bài tập hay nhất

Đề ôn tập Vật lí lớp 12

W 6 trang

Cực trị hàm số: Tài liệu chuyên đề chi tiết

Tài liệu chuyên đề: Cực trị hàm số

W 12 trang

Câu hỏi trắc nghiệm Toán lớp 11: Ôn tập hiệu quả

Câu hỏi trắc nghiệm ôn tập môn Toán lớp 11

5 trang

Tổng hợp lý thuyết Toán lớp 8: Tài liệu đầy đủ, chi tiết

Tài liệu Tổng hợp lý thuyết Toán lớp 8

W 16 trang

Tài liệu Lý thuyết và bài tập Tiếng Anh lớp 6

W 7 trang

Bài tập Đại số 7 cơ bản và nâng cao (Tài liệu dành cho giáo viên, phụ huynh)

Tài liệu Bài tập cơ bản và nâng cao Đại số 7 (Dành cho giáo viên, phụ huynh)

400 trang

Tài liệu bồi dưỡng học sinh giỏi môn Lịch sử lớp 9 (Sách Kết nối tri thức)

W 34 trang

Tài liệu Hình học 9 chương 5: Đường tròn - Tự luận có lời giải (Sách Kết nối tri thức với cuộc sống)

Tài liệu Hình học 9 - Chương 5: Đường tròn - Tự luận có lời giải (Sách Kết nối trí thức với cuộc sống)

181 trang

Phiếu bài tập cuối tuần Tiếng Việt lớp 1: Tổng hợp tuần 1 đến tuần 5

Phiếu bài tập cuối tuần Tiếng Việt 1 - Tuần 1 đến tuần 5

38 trang

AI tóm tắt

- Giúp bạn nắm bắt nội dung tài liệu nhanh chóng!

Giới thiệu tài liệu

Đối tượng sử dụng

Từ khoá chính

Nội dung tóm tắt

Giới thiệu

Về chúng tôi

Việc làm

Quảng cáo

Liên hệ

Chính sách

Thoả thuận sử dụng

Chính sách bảo mật

Chính sách hoàn tiền

DMCA

Hỗ trợ

Hướng dẫn sử dụng

Đăng ký tài khoản VIP

Zalo/Tel:

093 303 0098

Email:

[email protected]

Phương thức thanh toán

Theo dõi chúng tôi

Facebook

Youtube

TikTok

Chịu trách nhiệm nội dung: Nguyễn Công Hà Doanh nghiệp quản lý: Công ty TNHH Tài Liệu trực tuyến Vi Na - GCN ĐKDN: 0307893603 Địa chỉ: 54A Nơ Trang Long, P. Bình Thạnh, TP.HCM - Điện thoại: 0283 5102 888 - Email: [email protected]ấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015

Từ khóa » Tính Trung Bình Mẫu X Ngang