Từ Thông Và Suất điện động

TỪ THÔNG VÀ SUẤT ĐIỆN ĐỘNG XOAY CHIỀU

1. Cách tạo ra suất điện động xoay chiều:

Cho khung dây dẫn phẳng có N vòng ,diện tích S quay đều với vận tốc w, xung quanh trục vuông góc với với các đường sức từ của một từ trường đều có cảm ứng từ .Theo định luật cảm ứngđiện từ,trong khung dây xuất hiện một suất điện động biến đổi theo định luật dạng cosin với thời gian gọi tắt là suất điện động xoay chiều:

 

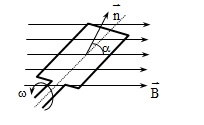
2.Từ thông gởi qua khung dây :

-Từ thông gửi qua khung dây dẫn gồm N vòng dây có diện tích S quay trong từ trường đều \(\vec{B}\).Giả sử tại t=0 thì : \((\vec{n},\vec{B})=\varphi\)

 - Biểu thức từ thông của khung: \(\Phi =NBScos\omega t=\Phi _{0}.cos\omega t\)

 - Từ thông qua khung dây cực đại  \(\Phi _{0}=NBS\); ω là tần số góc bằng tốc độ quay của khung (rad/s)

 Đơn vị : + Φ : Vêbe(Wb);                

               + S: Là diện tích một vòng dây (S:m2);

               + N: Số vòng dây của khung

             + \(\vec{B}\) : Véc tơ cảm ứng từ của từ trường đều .B:Tesla(T) ( \(\vec{B}\) vuông góc với trục quay ∆)

             + ω: Vận tốc góc không đổi của khung dây

            ( Chọn gốc thời gian t=0 lúc ( \((\vec{n},\vec{B})=0^{0}\))

 -Chu kì và tần số của khung :\(T=\frac{2\pi }{\omega };f=\frac{1}{T}\)

3. Suất điện động xoay chiều:

- Biểu thức của suất điện động cảm ứng tức thời:

\(e=\frac{-\Delta \Phi }{\Delta t}=-\Phi '=\omega NBS.sin\omega\)\(t=E_{o}cos(\omega t-\frac{\pi }{2})\)  

 \(e=E_{o}cos(\omega t+ \varphi _{0})\) Đặt  \(E_{0}=NB\omega S\) :Suất điện động cực đại  

 \(\varphi _{0}=\varphi -\frac{\pi }{2}\)

    Đơn vị :e,E0 (V)

VÍ DỤ MẪU:

Ví dụ 1: (CĐ 2009) Một khung dây dẫn phẳng dẹt hình chữ  nhật có 500 vòng dây, diện tích mỗi vòng 54 cm2. Khung dây quay đều quanh một trục đối xứng (thuộc mặt phẳng của khung), trong từ trường đều có vectơ cảm ứng từ vuông góc với trục quay và có độ lớn 0,2 T. Từ thông cực đại qua khung dây là

   A. 0,27 Wb.         B. 1,08 Wb .            C. 0,81 Wb.         D. 0,54 Wb.

Phân tích và hướng dẫn giải

Từ thông cực đại qua khung dây là: \(\Phi _{0}=NBS=500.0,2.54.10^{-4}=0,54Wb\) .

Chọn D

Ví dụ 2: (CĐ 2010) Một khung dây dẫn phẳng dẹt hình chữ nhật có 500 vòng dây, diện tích mỗi vòng là 220 cm2. Khung quay đều với tốc độ 50 vòng/giây quanh một trục đối xứng nằm trong mặt phẳng của khung dây, trong một từ trường đều có véc tơ cảm ứng từ  \(\vec{B}\) vuông góc với trục quay và có độ lớn \(\frac{\sqrt{2}}{5\pi }T\). Suất điện động cực đại trong khung dây bằng

          A. 110\(\sqrt{2}\)V.                B. 220\(\sqrt{2}\)V.              C. 110 V.             D. 220 V.

Phân tích và hướng dẫn giải

Tần số góc: \(\omega =50.2\pi =100\pi (rad/s)\).

Suất điện động cực đại trong khung dây bằng:

\(E_{0}=\omega NBS=100\pi .500.\frac{\sqrt{2}}{5\pi }.220.10^{-4}=220\sqrt{2}V\)

Chọn B

Ví dụ 3: (ĐH 2013)Một khung dây dẫn phẳng, dẹt, hình chữ nhật có diện tích 60 cm2, quay đều quanh một trục đối xứng (thuộc mặt phẳng của khung) trong từ trường đều có vectơ cảm ứng từ vuông góc với trục quay và có độ lớn 0,4 T. Từ thông cực đại qua khung dây là

          A. 2,4.10-3 Wb.           B. 1,2.10-3Wb.             C. 4,8.10-3Wb.          D. 0,6.10-3Wb.

Phân tích và hướng dẫn giải

Ta có:\(\Phi =\Phi _{0}cos(\omega t+\varphi )=BScos(\omega t+\varphi )\) .

Từ thông cực đại qua khung dây là: \(\Phi _{0}=BS=0,4.60.10^{-4}=2,4.10^{-3}Wb\).

Chọn A

Ví dụ 4: (ĐH 2009)

Từ thông qua một vòng dây dẫn là \(\Phi =\frac{2.10^{-2}}{\pi }cos(100\pi t+\frac{\pi }{4})(Wb)\) . Biểu thức của suất điện động cảm ứng xuất hiện trong vòng dây này là

          A.  \(e=-2sin(100\pi t+\frac{\pi }{4})(V)\)              B.\(e=2sin(100\pi t+\frac{\pi }{4})(V)\)

          C.\(e=-2sin100\pi t(V)\)                             D.\(e=2\pi sin100\pi t(V)\)

Phân tích và hướng dẫn giải

Suất điện động cảm ứng xuất hiện trong vòng dây:

\(e=-\frac{d\Phi }{dt}=100\pi .\frac{2.10^{-2}}{\pi }sin(100\pi t+\frac{\pi }{4})=2sin(100\pi t+\frac{\pi }{4})\)

 Chọn B

Ví dụ 5: (ĐH 2011)  Một khung dây dẫn phẳng quay đều với tốc độ góc ω quanh một trục cố định nằm trong mặt phẳng khung dây, trong một từ trường đều có vectơ cảm ứng từ vuông góc với trục quay của khung. Suất điện động cảm ứng trong khung có biểu thức e = E0cos(ωt + π/2 ). Tại thời điểm t = 0, vectơ pháp tuyến của mặt phẳng khung dây hợp với vectơ cảm ứng từ một góc bằng

          A. 1500.                    B. 900.                     C. 450.                  D. 1800.

Phân tích và hướng dẫn giải

Ta có:\(e=E_{0}sin(\omega t+\Phi )=E_{0}cos(\omega t+\Phi -\frac{\pi }{2})\) .

So sánh với biểu thức đề bài: \(e=E_{0}cos(\omega t+\frac{\pi }{2} )\Rightarrow \varphi -\frac{\pi }{2}=\frac{\pi }{2}\Rightarrow \varphi =\pi\)

Chọn D 

Ví dụ 6: Một khung dây dẫn hình chữ nhật, quay đều quanh trục đi qua trung điểm của hai cạnh đối diện của khung, trong một từ trường đều có véctơ cảm ứng từ \(\vec{B}\) vuông góc với trục quay của khung. Suất điện động cảm ứng xuất hiện trong khung dây đạt giá trị cực đại khi mặt khung

              A. vuông góc với \(\vec{B}\).                                    B. tạo với \(\vec{B}\) một góc 450               

              C. song song với \(\vec{B}\).                                     D. tạo với \(\vec{B}\) một góc 600           

Phân tích và hướng dẫn giải

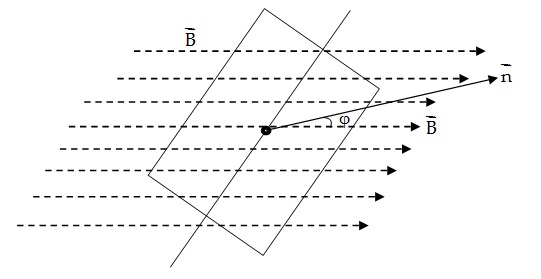
Suất điện động cảm ứng trong khung: \(e=E_{0}sin(\vec{B};\vec{n})\Rightarrow e=E_{0}\Rightarrow \vec{B};\vec{n}=\frac{\pi }{2}\)

Vì thế khi e max thì mặt phẳng khung song song với cảm ứng từ.

chọn C

Ví dụ 7: Một khung dây dẫn quay đều quanh trục xx’ với tốc độ 150 vòng/phút, trong một từ trường đều có véctơ cảm ứng từ vuông góc với trục quay xx’ của khung. Ở thời điểmnào đó từ thông gửi qua khung dây  là 0,4Wb thì suất điện động cảm ứng xuất hiện trong khung dây bằng 47V. Từ thông cực đại gửi qua khung dây bằng

A. 0,4Wb.                 B. 0,4πWb.                  C. 0,5Wb.                        D. 0,5πWb.

Phân tích và hướng dẫn giải

Tần số góc dao động của khung:

 

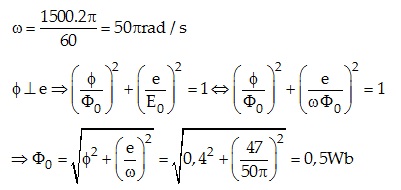
Ví dụ 8: Một vòng dây có diện tích S=100cm2  và điện trở R=0,45Ω , quay đều với tốc độ góc ω=100 rad/s  trong một từ trường đều có cảm ứng từ  B=0,1T xung quanh một trục nằm trong mặt phẳng vòng dây và vuông góc với các đường sức từ. Nhiệt lượng tỏa ra trong vòng dây khi nó quay được 1000 vòng  là:

          A. 1,39J.                      B. 7J.                  C. 0,7J.                   D. 0,35J.

Phân tích và hướng dẫn giải

Suất điện động cực đại: \(E_{0}=\omega NBS=0,1V\) .

Dòng điện chạy trên vòng dây \(I=\frac{E_{0}}{\sqrt{2}R}\)

Nhiệt lượng tỏa ra \(Q=I^{2}Rt=(\frac{{E_{0}}^{2}}{2R}).t\)

Thời gian quay được 1000 vòng: \(t=20\pi s ;Q=0,7J\)

Chọn C

Ví dụ 9: (Trích đề thi thử chuyên Vĩnh Phúc lần 2 năm 2014)

Một cuộn dây dẫn dẹt, quay đều quanh một trục cố định trong từ trường đều có phương vuông góc với trục quay. Suất điện động cảm ứng xuất hiện trong cuộn dây có giá trị cực đại là E0. Tại thời điểm suất điện động tức thời bằng e = E0/2 và đang tăng thì véc tơ pháp tuyến \(\vec{n}\) hợp với véc tơ \(\vec{B}\) một góc bằng

              A. 1500.                  B. 1200.             C. 300                   D. 600.

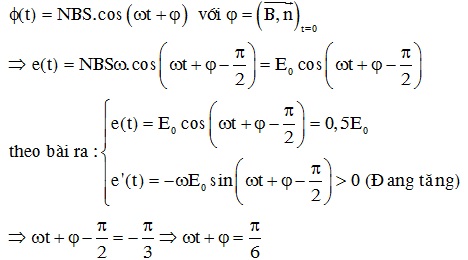
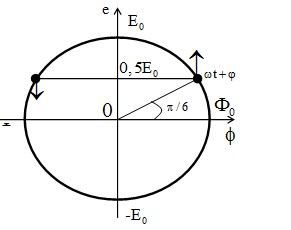
bài toán giải nhanh hơn với

vòng tròn lượng giác.

Suất điện động trễ pha 900 so với từ thông nên hai đại

 lượng này được biểu diễn trong vòng tròn như hình vẽ.

Từ hình vẽ ta thấy: \(\omega t+\varphi =\frac{\pi }{6}\)

Chọn C

BÀI TẬP VẬN DỤNG:

Câu 1:(CĐ 2013) Một vòng dây dẫn phẳng có diện tích 100 cm2, quay đều quanh một trục đối xứng (thuộc mặt phẳng của vòng dây), trong từ trường đều có vectơ cảm ứng từ vuông góc với trục quay. Biết từ thông cực đại qua vòng dây là 0,004Wb . Độ lớn của cảm ứng từ là:

            A. 0,2T                 B. 0,6T                     C. 0,8T                   D. 0,4T

Hướng dẫn giải

Từ thông cực đại qua vòng dây:

\(\Phi _{0}=BS\Rightarrow B=\frac{\Phi _{0}}{S}=\frac{0,004}{100.10^{-4}}=0,4T\)

Chọn D

Câu 2: (trích đề thi thử chuyên Đại Học Vinh lần 3 năm 2014)Một khung dây dẫn kín hình chữ nhật có thể quay đều quanh trục đi qua trung điểm hai cạnh đối diện, trong một từ trường đều có cảm ừng từ \(\vec{B}\) vuông góc với trục quay. Suất điện động xoay chiều xuất hiện trong khung có giá trị cực đại khi mặt khung

             A. song song với \(\vec{B}\)                                    B. vuông góc với  \(\vec{B}\)             

             C. tạo với \(\vec{B}\) một góc 450.                          D. tạo với \(\vec{B}\) một góc 600.

Hướng dẫn giải

 \(e=-\Phi ;=E_{0}sin(\omega t+\varphi )\Rightarrow e=E_{0}\Leftrightarrow \omega t+\varphi =\frac{\pi }{2}\Rightarrow \vec{n}// \vec{B}\)

Chọn A

Câu 3: (CĐ 2011) Một khung dây dẫn phẳng, hình chữ nhật, diện tích 0,025 m2, gồm 200 vòng dây quay đều với tốc độ 20 vòng/s quanh một trục cố định trong một từ trường đều. Biết trục quay là trục đối xứng nằm trong mặt phẳng khung và vuông góc với phương của từ trường. Suất điện động hiệu dụng xuất hiện trong khung có độ lớn bằng 222 V. Cảm ứng từ có độ lớn bằng

         A. 0,45 T.                 B. 0,60 T.                  C. 0,50 T.               D. 0,40 T.

Hướng dẫn giải

Tần số góc:\(\omega =20.2\pi =40\pi (rad/s)\).

Suất điện động cực đại trong khung dây bằng:

\(E_{0}=\omega NBS\Rightarrow B=\frac{E_{0}}{\omega NS}=\frac{E\sqrt{2}}{\omega NS}=\frac{220\sqrt{2}}{40\pi .200.0,025}=0,5T\)

Chọn C

Câu 4: Một khung dây dẫn phẳng dẹt hình chữ nhật có 500 vòng dây, diện tích mỗi vòng là 220 cm2. Khung quay đều với tốc độ 50 vòng/giây quanh một trục đối xứng nằm trong mặt phẳng của khung dây, trong một từ trường đều có véc tơ cảm ứng từ \(\vec{B}\) vuông góc với trục quay và có độ lớn B. Để tạo ra suất điện động hiệu dụng có giá trị là E = 220V thì cảm ứng từ B có độ lớn là

              A. \(\frac{\sqrt{3}}{\pi }\).                        B. \(\frac{\sqrt{2}}{5\pi }\)T.                      C. \(\frac{\sqrt{2}}{\pi }\) T                 D. \(\frac{\sqrt{5}}{5\pi }\).

Hướng dẫn giải

Tần số quay của khung là  \(f=50\frac{vong}{giay}=50Hz\Rightarrow \omega =100\pi (rad/s)\)

Suất điện động của máy phát điện xoay chiều một pha:

 \(E=\frac{NBS\omega }{\sqrt{2}}\Rightarrow B=\frac{E\sqrt{2}}{NS\omega }=\frac{220\sqrt{2}}{500.220.10^{-4}.100\pi }=\frac{\sqrt{2}}{5\pi }(T)\)

Chọn B 

Câu 5: Một khung dây dẫn phẳng quay đều với tốc độ góc w quanh một trục cố định nằm trong mặt phẳng khung dây, trong một từ trường đều có vectơ cảm ứng từ vuông góc với trục quay của khung. Suất điện động cảm ứng trong khung có biểu thức e =\(E_{0}cos(\omega t)\) . Biểu thức của từ thông gửi qua khung dây là

           A. \(\Phi =\frac{E_{0}}{\omega }cos(\omega t-\frac{\pi }{2})\).                             B. \(\Phi =\omega E_{0}cos(\omega t-\frac{\pi }{2})\).

           C.\(\Phi =\omega E_{0}cos(\omega t+\frac{\pi }{2})\) .                            D. \(\Phi =\frac{E_{0}}{\omega }cos(\omega t+\frac{\pi }{2})\).

Hướng dẫn giải

Ta biết rằng, suất điện động cảm ứng trong khung chậm pha hơn từ thông cảm ứng  gửi qua khung là \(\frac{\pi }{2}\) vì thế ta có: \(\varphi _{\Phi }=\varphi _{e}+\frac{\pi }{2}=8+\frac{\pi }{2}=\frac{\pi }{2}\)

 \(\Rightarrow \Phi =\Phi _{0}cos(\omega t+\frac{\pi }{2})(Wb)=\frac{E_{0}}{\omega }cos(\omega t+\frac{\pi }{2})(Wb)\)

Chọn D