Tương Tác Từ - Định Luật Ampère | Vật Lý Đại Cương

Xét dòng điện I chạy trong dây dẫn có tiết diện ngang S rất nhỏ. Trên dây dẫn đó, lấy một độ dời vi phân  \( d\overrightarrow{\ell } \) theo chiều của dòng điện. Ta gọi tích số  \( Id\overrightarrow{\ell } \) là một phần tử dòng điện hau một yếu tố dòng điện. Phần tử dòng điện là đại lượng vectơ có độ lớn bằng \(Id\ell \), có phương tiếp tuyến với dây dẫn tại điểm khảo sát và có chiều của dòng điện (hình 4.1)

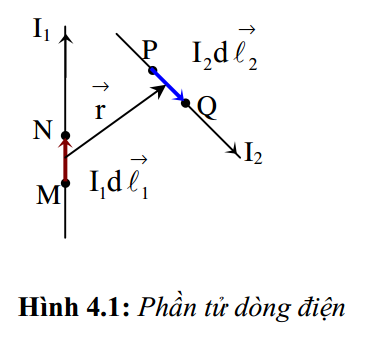
Xét hai phần tử dòng điện \({{I}_{1}}d{{\overrightarrow{\ell }}_{1}}\) và \({{I}_{2}}d{{\overrightarrow{\ell }}_{2}}\) của hai dòng điện I1 và I2 đặt trong chân không. Gọi  \( \vec{r} \) là vectơ khoảng cách hướng từ \({{I}_{1}}d{{\overrightarrow{\ell }}_{1}}\) đến \({{I}_{2}}d{{\overrightarrow{\ell }}_{2}}\). Vẽ mặt phẳng (P) chứa \({{I}_{1}}d{{\overrightarrow{\ell }}_{1}}\) và \(\vec{r}\). Quy ước pháp vectơ đơn vị  \( \vec{n} \) của mặt phẳng (P) có chiều sao cho khi xoay cái đinh ốc từ vectơ \({{I}_{1}}d{{\overrightarrow{\ell }}_{1}}\) đến vectơ  \( \vec{r} \) theo góc nhỏ nhất thì chiều tiến của cái đỉnh ốc là chiều của vectơ \(\vec{n}\) (hình 4.2).

Lực tương tác giữa hai phần tử dòng điện này tuân theo định luật Ampère: lực từ do phần tử dòng điện \({{I}_{1}}d{{\overrightarrow{\ell }}_{1}}\) tác dụng lên phần tử dòng điện \({{I}_{2}}d{{\overrightarrow{\ell }}_{2}}\) là một vectơ  \( d\overrightarrow{F} \) có:

+ Phương: vuông góc với mặt phẳng chứa yếu tố dòng \({{I}_{2}}d{{\overrightarrow{\ell }}_{2}}\) và vectơ  \( \vec{n} \);

+ Chiều: xác định theo quy tắc cái định ốc “xoay cái đinh ốc từ \({{I}_{2}}d{{\overrightarrow{\ell }}_{2}}\) đến vectơ  \( \vec{n} \) theo góc nhỏ nhất thì chiều tiến của cái đinh ốc là chiều của vectơ  \( d\overrightarrow{F} \)”.

+ Độ lớn:  \( dF=\frac{{{\mu }_{0}}{{I}_{1}}{{I}_{2}}d{{\ell }_{1}}d{{\ell }_{2}}\sin {{\theta }_{1}}\sin {{\theta }_{2}}}{4\pi {{r}^{2}}} \)     (4.1)

+ Điểm đặt: tại yếu tố dòng \({{I}_{2}}d{{\overrightarrow{\ell }}_{2}}\).

Trong (4.1),  \( {{\mu }_{0}} \) là hằng số từ, có giá trị:  \( {{\mu }_{0}}=4\pi {{.10}^{-7}}\text{ }H/m  \).

Có thể viết công thức của định luật Ampère dưới dạng vectơ:  \( d\overrightarrow{F}=\frac{{{\mu }_{0}}}{4\pi }\frac{{{I}_{2}}d{{\overrightarrow{\ell }}_{2}}\times \left( {{I}_{1}}d{{\overrightarrow{\ell }}_{1}}\times \vec{r} \right)}{{{r}^{3}}} \)    (4.2)

Thực nghiệm chứng tỏ rằng, nếu hai dòng điện và I2 đặt trong môi trường đồng chất đẳng hướng thì lực từ tăng  \( \mu  \) lần so với khi chúng đặt trong chân không:

 \( d\overrightarrow{F}=\mu .d{{\overrightarrow{F}}_{ck}}=\frac{{{\mu }_{0}}\mu }{4\pi }\frac{{{I}_{2}}d{{\overrightarrow{\ell }}_{2}}\times \left( {{I}_{1}}d{{\overrightarrow{\ell }}_{1}}\times \vec{r} \right)}{{{r}^{3}}} \)      (4.3)

Hệ số  \( \mu  \) được gọi là hệ số từ thẩm hay độ từ thẩm của môi trường. Đối với chân không thì  \( \mu =1 \); các chất sắt từ thì  \( \mu >>1 \); đối với các chất thuận từ hoặc nghịch từ giá trị  \( \mu  \) dao động hơn kém xung quanh đơn vị một lượng nhỏ ( \( \mu \approx 1 \)). Vì thế, trong đa số các trường hợp, ta bỏ qua hệ số \( \mu \).

Về hình thức, điện và từ giống như hai bàn tay của một cơ thể người. Mỗi đại lượng đặc trưng cho điện đều tương ứng với một đại lượng đặc trưng cho từ. Ví dụ: hằng số điện  \( {{\varepsilon }_{0}} \) tương ứng với hằng số từ  \( {{\mu }_{0}} \); hệ số điện môi  \( \varepsilon  \) tương ứng với hệ số từ thẩm  \( \mu  \); định luật Ampère có vai trò như định luật Coulomd; yếu tố dòng điện  \( Id\overrightarrow{\ell } \) có vai trò như điện tích điểm q, … Nắm được tính chất này, ta sẽ tìm hiểu từ trường một cách hiệu quả hơn.