Viết Phương Trình Tiếp Tuyến Của đường Tròn Song Song Với đường ...

KhoiA.Vn sẽ giới thiệu với các em cách viết viết phương trình tiếp tuyến của đường tròn vuông góc với đường thẳng cho trước qua bài này một cách ngắn gọn, chi tiết và đẩy đủ để các em tham khảo.

I. Cách viết phương trình tiếp tuyến của đường tròn song song với đường thẳng

Giả sử đường tròn (C) có tâm I(a; b); bán kính R và và đường thẳng (d) cho trước

Viết phương trình tiếp tuyến của (C) song song với đường thẳng (d):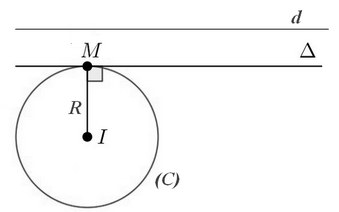

Để viết phương trình tiếp tuyến Δ của đường tròn (C) song song với đường thẳng (d): Ax + By + C = 0 ta thực hiện như sau:

- Bước 1: Xác định tâm I và bán kính R của đường tròn (C).

- Bước 2: Vì Δ // (d): Ax + By + C = 0 nên Δ có vectơ pháp tuyến là vectơ pháp tuyến của (d): 

 Khi đó phương trình tiếp tuyến Δ có dạng: Ax + By + c1 = 0 (c1 ≠ C)

- Bước 3: Vì Δ tiếp xúc với đường tròn (C) nên d(I,Δ) = R. Giải phương trình này ta tìm được c1.

II. Bài tập vận dụng viết phương trình tiếp tuyến của đường tròn song song với đường thẳng

* Bài tập 1: Cho đường tròn (C) có phương trình: (x - 3)2 + (y + 1)2 = 5. Viết phương trình tiếp tuyến của (C) song song với đường thẳng (d): 2x + y + 9 = 0.

> Lời giải:

- Đường tròn (C) có tâm I(3; -1) và bán kính R = √5

- Vì tiếp tuyến Δ cần tìm song song với đường thẳng (d): 2x + y + 9 = 0 nên 

Khi đó phương trình tiếp tuyến của ∆ có dạng: 2x + y + c = 0 với c ≠ 9.

- Vì đường thẳng Δ tiếp xúc với đường tròn (C) nên có: d(I,Δ) = R

Vậy có 2 phương trình tiếp tuyến thỏa điều kiện bài toán là:

2x + y = 0  và 2x + y - 10 = 0.

* Bài tập 2: Viết phương trình tiếp tuyến của đường tròn (C): x2 + y2 - 2x + 6y - 6 = 0. Biết tiếp tuyến song song với đường thẳng (d): 6x - 8y - 3 = 0

> Lời giải:

- Ta có: x2 + y2 - 2x + 6y - 6 = 0

⇔ x2 - 2x + 1 + y2 + 2.3y + 9 = 16

⇔ (x - 1)2 + (y + 3)2 = 16

- Đường tròn (C) có tâm I(1; -3) bán kính R = 4.

- Vì tiếp tuyến Δ cần tìm song song với đường thẳng (d): 6x - 8y - 3 = 0 nên

Khi đó phương trình tiếp tuyến của ∆ có dạng: 3x - 4y + c = 0 với c ≠ 3.

- Vì đường thẳng Δ tiếp xúc với đường tròn (C) nên có: d(I,Δ) = R

 

Vậy có 2 tiếp tuyến thỏa yêu cầu bài toán là:

 3x - 4y + 5 = 0 và 3x - 4y - 35 = 0.

* Bài tập 3: Cho đường tròn (C): x2 + y2 + 2x - 6y + 5 = 0 . Viết phương trình tiếp tuyến của (C) song song với đường thẳng d: x + 2y - 7 = 0.

> Lời giải:

- Ta có: Đường tròn ( C) có tâm I(-1;3) và bán kính

 

- Vì tiếp tuyến cần tìm song song với đường thẳng (d): x + 2y - 7 = 0 nên