Vòng Tròn Lượng Giác

Có thể bạn quan tâm

Vòng tròn lượng giác hay đường tròn lượng giác là một công cụ toán học cơ bản giúp xác định các giá trị của các hàm số lượng giác như sin, cos và tan tại các góc khác nhau.

Vòng tròn lượng giác là một trong những công cụ không thể thiếu trong nhiều bài toán và ứng dụng thực tế, nhất là trong các lĩnh vực toán học và vật lý. Vòng tròn lượng giác giúp chúng ta giải các bài toán đạo động điều hòa, nơi mà vị trí và vận tốc của một hệ vật lý có thể được biểu diễn bằng các phương trình lượng giác. Vậy sau đây là trọn bộ nội dung chi tiết kiến thức về Vòng tròn lượng giác mời các bạn cùng theo dõi tại đây.

Vòng tròn lượng giác chi tiết nhất

1. Vòng tròn lượng giác là gì?
2. Cách sử dụng vòng tròn lượng giác
3. Dấu của các giá trị lượng giác
4. Bảng giá trị lượng giác từ đến
5. Công thức các cung liên kết trên đường tròn lượng giác
6. Ứng dụng của vòng tròn lượng giác
7. Bài tập vận dụng vòng tròn lượng giác

1. Vòng tròn lượng giác là gì?

Theo lý thuyết, một dao động điều hòa có phương trình x = Acos(ωt + φ) có thể biểu diễn bằng 1 vòng tròn lượng giác. Dựa vào hình học biểu diễn trên đường tròn kết hợp với công thức lượng giác ta có thể suy ra những đại lượng vật lý cần tìm như biên độ A, li độ x, thời gian t,… tùy theo dữ kiện cho và câu hỏi đặt ra.

2. Cách sử dụng vòng tròn lượng giác

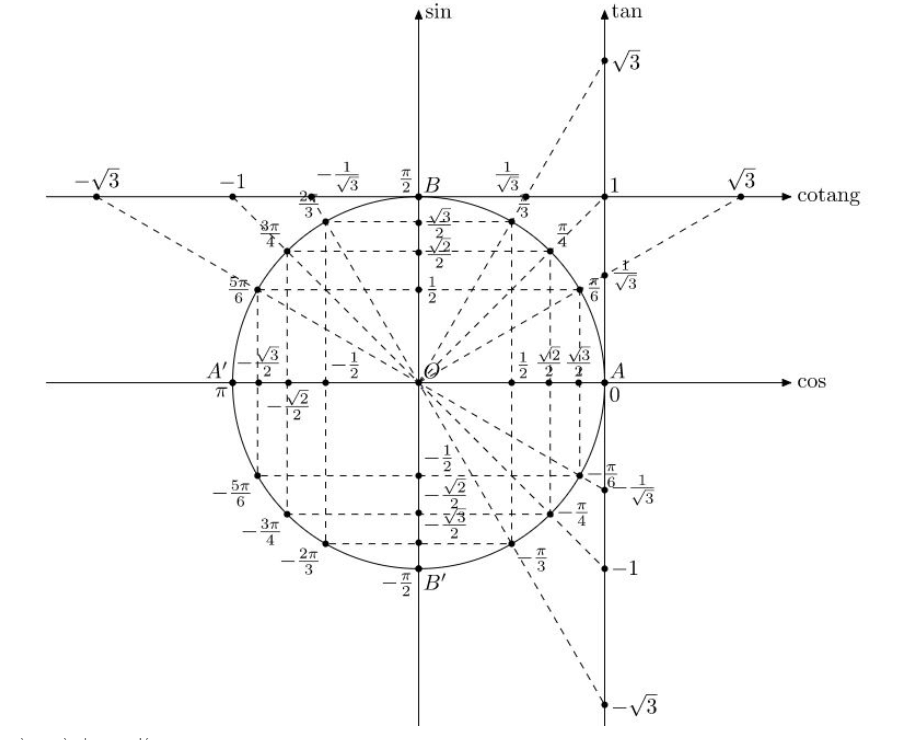
- Vòng tròn lượng giác là đường tròn đơn vị tâm O bán kính 1, định hướng với quy ước chiều dương là chiều ngược chiều kim đồng hồ và trên đó A là điểm gốc.

- Điểm $P\left( x,y \right)$ $P\left( x,y \right)$ trên đường tròn lượng giác sao cho một điểm C bất kì nằm trên đường tròn ta đều có $\left( OA,OC \right)=\alpha$ $\left( OA,OC \right)=\alpha$ được gọi là điểm trên đường tròn lượng giác biểu diễn cung lượng giác có số đo $\alpha$ $\alpha$.

- Trục Ox được gọi là trục giá trị cos.

- Trục Oy được gọi là trục giá trị sin.

- Trục tan có gốc là điểm và vuông góc với trục cos, trục cotan có gốc là điểm vuông góc với trục sin.

3. Dấu của các giá trị lượng giác

Các giá trị của vòng tròn lượng giác sẽ gồm có dấu, bảng giá trị lượng giác từ 0 - 180 độ. Ngoài ra các em cũng cần nắm rõ công thức về các cung liên kết với vòng tròn lượng giác. Cụ thể như sau:

Dấu của giá trị lượng giác

Các giá trị lượng giác trong vòng tròn lượng giác, cũng như các góc ¼ số cụ thể như sau:

Giá trị lượng giác Sinx, góc phần tư thứ nhất và góc phần tư thứ 2 mang dấu (+), góc phần tư thứ 3 và góc phần thứ 4 mang dấu (-).
Giá trị lượng giác Cosx, góc phần tư thứ nhất và góc phần tư thứ 4 mang dấu (+), góc phần tư thứ 2 và góc phần tư thứ 3 mang dấu (-).
Giá trị Tanx, góc phần tư thứ nhất và góc phần tư thứ 3 mang dấu (+), góc phần tư thứ 2 và góc phần tư thứ 4 mang dấu (-).
Giá trị Cotx, góc phần thứ nhất nhất và góc phần thứ thứ 3 mang dấu (+), góc phần tư thứ 2 và góc phần tư thứ 4 mang dấu (-).

Để giúp các em dễ dàng ghi nhớ về dấu giá trị lượng giác, dưới đây là bảng tổng hợp ngắn gọn như sau:

Góc phần tư số	I	II	III	IV
Giá trị lượng giác	I	II	III	IV
sin x	+	+	-	-
cos x	+	-	-	+
tan x	+	-	+	-
cot x	+	-	+	-

4. Bảng giá trị lượng giác từ ${{0}^{0}}$ ${{0}^{0}}$ đến ${{180}^{0}}$ ${{180}^{0}}$

$\alpha$ $\alpha$	$0$ $\left( {{0}^{0}} \right)$ $\left( {{0}^{0}} \right)$	$\frac{\pi }{6}$ $\frac{\pi }{6}$ $\left( {{30}^{0}} \right)$ $\left( {{30}^{0}} \right)$	$\frac{\pi }{4}$ $\frac{\pi }{4}$ $\left( {{45}^{0}} \right)$ $\left( {{45}^{0}} \right)$	$\frac{\pi }{3}$ $\frac{\pi }{3}$ $\left( {{60}^{0}} \right)$ $\left( {{60}^{0}} \right)$	$\frac{\pi }{2}$ $\frac{\pi }{2}$ $\left( {{90}^{0}} \right)$ $\left( {{90}^{0}} \right)$	$\frac{2\pi }{3}$ $\frac{2\pi }{3}$ $\left( {{120}^{0}} \right)$ $\left( {{120}^{0}} \right)$	$\frac{3\pi }{4}$ $\frac{3\pi }{4}$ $\left( {{135}^{0}} \right)$ $\left( {{135}^{0}} \right)$	$\frac{5\pi }{6}$ $\frac{5\pi }{6}$ $\left( {{150}^{0}} \right)$ $\left( {{150}^{0}} \right)$	$\pi$ $\pi$ $\left( {{180}^{0}} \right)$ $\left( {{180}^{0}} \right)$	$\frac{3\pi }{2}$ $\frac{3\pi }{2}$ $\left( {{270}^{0}} \right)$ $\left( {{270}^{0}} \right)$	$2\pi$ $2\pi$ $\left( {{360}^{0}} \right)$ $\left( {{360}^{0}} \right)$
$\sin \alpha$ $\sin \alpha$	0	$\frac{1}{2}$ $\frac{1}{2}$	$\frac{\sqrt{2}}{2}$ $\frac{\sqrt{2}}{2}$	$\frac{\sqrt{3}}{2}$ $\frac{\sqrt{3}}{2}$	$1$	$\frac{\sqrt{3}}{2}$ $\frac{\sqrt{3}}{2}$	$\frac{\sqrt{2}}{2}$ $\frac{\sqrt{2}}{2}$	$\frac{1}{2}$ $\frac{1}{2}$	0	-1	0
$\cos \alpha$ $\cos \alpha$	1	$\frac{\sqrt{3}}{2}$ $\frac{\sqrt{3}}{2}$	$\frac{\sqrt{2}}{2}$ $\frac{\sqrt{2}}{2}$	$\frac{1}{2}$ $\frac{1}{2}$	0	$-\frac{1}{2}$ $-\frac{1}{2}$	$-\frac{\sqrt{2}}{2}$ $-\frac{\sqrt{2}}{2}$	$-\frac{\sqrt{3}}{2}$ $-\frac{\sqrt{3}}{2}$	-1	0	1
$\tan \alpha$ $\tan \alpha$	0	$\frac{1}{\sqrt{3}}$ $\frac{1}{\sqrt{3}}$	1	$\sqrt{3}$ $\sqrt{3}$	\|\|	$-\sqrt{3}$ $-\sqrt{3}$	-1	$-\frac{1}{\sqrt{3}}$ $-\frac{1}{\sqrt{3}}$	0	\|\|	0
$\cot \alpha$ $\cot \alpha$	\|\|	$\sqrt{3}$ $\sqrt{3}$	1	$\frac{1}{\sqrt{3}}$ $\frac{1}{\sqrt{3}}$	0	$-\frac{1}{\sqrt{3}}$ $-\frac{1}{\sqrt{3}}$	-1	$-\sqrt{3}$ $-\sqrt{3}$	\|\|	0	\|\|

5. Công thức các cung liên kết trên đường tròn lượng giác

Góc đối nhau ( cos đối)	Góc bù nhau (sin bù)	Góc phụ nhau (Phụ chéo)	Góc hơn kém (Khác pi tan)
cos (-α) = cos α	sin (π-α) = sin α	sin (π/2-α)= cos α	sin (π+α) = - sin α
sin (-α) = -sin α	cos (π-α) = - cos α	cos (π/2-α) = sinα	cos (π+α) = - cosα
tan (-α) = - tan α	tan (π-α) = - tan α	tan (π/2-α) = cot α	tan (π+α) = tanα
cot (-α) = -cot α	cot (π-α) = – cot α	cot (π/2-α) = tan α	cot (π+α) = cotα

6. Ứng dụng của vòng tròn lượng giác

Toán học: Trong toán học, vòng tròn lượng giác giúp giải các bài toán hình học và phương trình lượng giác. Nó cũng là công cụ cơ bản để xác định các giá trị sin, cos, tan và các hàm lượng giác khác cho bất kỳ góc nào.
Vật lý: Trong vật lý, vòng tròn lượng giác rất quan trọng trong việc phân tích các chuyển động tròn đều và dao động điều hòa. Các hàm lượng giác được sử dụng để mô tả các đại lượng vật lý như vận tốc, gia tốc trong các bài toán về sóng và dao động.

Vòng tròn lượng giác cũng hữu ích trong việc giải các bài toán đạo động điều hòa, nơi mà vị trí và vận tốc của một hệ vật lý có thể được biểu diễn bằng các phương trình lượng giác. Ví dụ, vị trí (x) và vận tốc (v) của một vật dao động điều hòa có thể được mô tả bằng phương trình x = A*cos(ωt + φ) và v = -ωA*sin(ωt + φ).

7. Bài tập vận dụng vòng tròn lượng giác

Câu 1: Trên đường tròn lượng giác cho các cung lượng giác (I), (II), (III) và (IV) có điểm đầu là A và có số đo lần lượt là:

(a) $\frac{\pi }{4}$ $\frac{\pi }{4}$

(b) $- \frac{{7\pi }}{4}$ $- \frac{{7\pi }}{4}$

(d) $- \frac{{71\pi }}{4}$ $- \frac{{71\pi }}{4}$

Hỏi các cung nào có điểm cuối trùng nhau?

A. Chỉ (a) và (b)

B. Chỉ (a), (b), (c)

C. Chỉ (b), (c), (d)

D. Chỉ (a), (b) và (d)

Câu 2: Biết một góc lượng giác (Ou, Ov) có số đo $\frac{{ - 138\pi }}{5}$ $\frac{{ - 138\pi }}{5}$. Góc lượng giác (Ou, Ov) âm lớn nhất là:

A. -1,6π

B. -27,6π

C. -0,6π

D. -0,4π

Câu 3: Trên đường tròn lượng giác, số các điểm ngọn của cung có số đo bằng $\frac{\pi }{6} + \frac{{k2\pi }}{5}$ $\frac{\pi }{6} + \frac{{k2\pi }}{5}$ là:

A. 2

B. 3

C. 5

D. 6

Câu 4: Trên đường tròn lượng giác, điểm ngọn của cung có số đo 30000 nằm ở góc phần tư thứ mấy?

A. I

B. II

C. III

D. IV

Câu 5: Cho góc α biết $\pi < \alpha < \frac{{3\pi }}{2}$ $\pi < \alpha < \frac{{3\pi }}{2}$, chọn đáp án đúng trong các đáp án dưới đây?

A. cos α > 0, sin α > 0	B. cos α > 0, sin α < 0
C. cos α < 0, sin α > 0	D. cos α < 0, sin α < 0

Từ khóa » Cách Vẽ Vòng Tròn Lượng Giác Vật Lý 12

$\alpha$ \(\alpha\)	\(0\) $\left( {{0}^{0}} \right)$ \(\left( {{0}^{0}} \right)\)	$\frac{\pi }{6}$ \(\frac{\pi }{6}\) $\left( {{30}^{0}} \right)$ \(\left( {{30}^{0}} \right)\)	$\frac{\pi }{4}$ \(\frac{\pi }{4}\) $\left( {{45}^{0}} \right)$ \(\left( {{45}^{0}} \right)\)	$\frac{\pi }{3}$ \(\frac{\pi }{3}\) $\left( {{60}^{0}} \right)$ \(\left( {{60}^{0}} \right)\)	$\frac{\pi }{2}$ \(\frac{\pi }{2}\) $\left( {{90}^{0}} \right)$ \(\left( {{90}^{0}} \right)\)	$\frac{2\pi }{3}$ \(\frac{2\pi }{3}\) $\left( {{120}^{0}} \right)$ \(\left( {{120}^{0}} \right)\)	$\frac{3\pi }{4}$ \(\frac{3\pi }{4}\) $\left( {{135}^{0}} \right)$ \(\left( {{135}^{0}} \right)\)	$\frac{5\pi }{6}$ \(\frac{5\pi }{6}\) $\left( {{150}^{0}} \right)$ \(\left( {{150}^{0}} \right)\)	$\pi$ \(\pi\) $\left( {{180}^{0}} \right)$ \(\left( {{180}^{0}} \right)\)	$\frac{3\pi }{2}$ \(\frac{3\pi }{2}\) $\left( {{270}^{0}} \right)$ \(\left( {{270}^{0}} \right)\)	$2\pi$ \(2\pi\) $\left( {{360}^{0}} \right)$ \(\left( {{360}^{0}} \right)\)
$\sin \alpha$ \(\sin \alpha\)	0	$\frac{1}{2}$ \(\frac{1}{2}\)	$\frac{\sqrt{2}}{2}$ \(\frac{\sqrt{2}}{2}\)	$\frac{\sqrt{3}}{2}$ \(\frac{\sqrt{3}}{2}\)	\(1\)	$\frac{\sqrt{3}}{2}$ \(\frac{\sqrt{3}}{2}\)	$\frac{\sqrt{2}}{2}$ \(\frac{\sqrt{2}}{2}\)	$\frac{1}{2}$ \(\frac{1}{2}\)	0	-1	0
$\cos \alpha$ \(\cos \alpha\)	1	$\frac{\sqrt{3}}{2}$ \(\frac{\sqrt{3}}{2}\)	$\frac{\sqrt{2}}{2}$ \(\frac{\sqrt{2}}{2}\)	$\frac{1}{2}$ \(\frac{1}{2}\)	0	$-\frac{1}{2}$ \(-\frac{1}{2}\)	$-\frac{\sqrt{2}}{2}$ \(-\frac{\sqrt{2}}{2}\)	$-\frac{\sqrt{3}}{2}$ \(-\frac{\sqrt{3}}{2}\)	-1	0	1
$\tan \alpha$ \(\tan \alpha\)	0	$\frac{1}{\sqrt{3}}$ \(\frac{1}{\sqrt{3}}\)	1	$\sqrt{3}$ \(\sqrt{3}\)	\|\|	$-\sqrt{3}$ \(-\sqrt{3}\)	-1	$-\frac{1}{\sqrt{3}}$ \(-\frac{1}{\sqrt{3}}\)	0	\|\|	0
$\cot \alpha$ \(\cot \alpha\)	\|\|	$\sqrt{3}$ \(\sqrt{3}\)	1	$\frac{1}{\sqrt{3}}$ \(\frac{1}{\sqrt{3}}\)	0	$-\frac{1}{\sqrt{3}}$ \(-\frac{1}{\sqrt{3}}\)	-1	$-\sqrt{3}$ \(-\sqrt{3}\)	\|\|	0	\|\|

Vòng Tròn Lượng Giác

Vòng tròn lượng giác chi tiết nhất

1. Vòng tròn lượng giác là gì?

2. Cách sử dụng vòng tròn lượng giác

3. Dấu của các giá trị lượng giác

Dấu của giá trị lượng giác

4. Bảng giá trị lượng giác từ ${{0}^{0}}$ \({{0}^{0}}\) đến ${{180}^{0}}$ \({{180}^{0}}\)

5. Công thức các cung liên kết trên đường tròn lượng giác

6. Ứng dụng của vòng tròn lượng giác

7. Bài tập vận dụng vòng tròn lượng giác

Phương Pháp Đường Tròn Lượng Giác Vật Lý 12 - Kiến Guru

Ứng Dụng Vòng Tròn Lượng Giác Vào Bài Toán Về DĐĐH - YouTube

[CHUẨN NHẤT] Ứng Dụng Vòng Tròn Lượng Giác Vật Lý - TopLoigiai

Sử Dụng Vòng Tròn Lượng Giác Trong Vật Lý 12

Vòng Tròn Lượng Giác Trong Vật Lý 12 - Diện Tích

Phương Pháp Sử Dụng Đường Tròn Lượng Giác Trong Dao động điều ...

ỨNG DỤNG CỦA VÒNG TRÒN LƯỢNG GIÁC TRONG DAO ĐỘNG ...

Kiến Thức Cần Nhớ: Đường Tròn Lượng Giác Vật Lý 12 | Lessonopoly

Ứng Dụng Vòng Tròn Lượng Giác Phá đảo Vật Lí 12 - Giáo Viên Việt Nam

Vòng Tròn Lượng Giác Vật Lý 12 - Hàng Hiệu

Sử Dụng đường Tròn Pha Trong Dao động điều Hòa - Vật Lí Phổ Thông

Bài Tập áp Dụng Vòng Tròn Lượng Giác - Tài Liệu - 123doc

Vòng Tròn Lượng Giác Vật Lý 12, Vòng Tròn Lượng Giác

Liên Hệ

Vòng tròn lượng giác chi tiết nhất

1. Vòng tròn lượng giác là gì?

2. Cách sử dụng vòng tròn lượng giác

3. Dấu của các giá trị lượng giác

Dấu của giá trị lượng giác

4. Bảng giá trị lượng giác từ \({{0}^{0}}\) đến \({{180}^{0}}\)

5. Công thức các cung liên kết trên đường tròn lượng giác

6. Ứng dụng của vòng tròn lượng giác

7. Bài tập vận dụng vòng tròn lượng giác

Liên Hệ

4. Bảng giá trị lượng giác từ ${{0}^{0}}$ \({{0}^{0}}\) đến ${{180}^{0}}$ \({{180}^{0}}\)