What Is The PSD? - Power Spectral Density

Getting Started

Introduction to Random Vibration Testing

Power Spectral Density

Random Testing and the Power Spectral Density (PSD)

What is the PSD?

How to Compute the PSD

Calculating PSD from a Time-history File

Converting Recorded Data

The FFT and Digital Sampling

Aliasing

Windowing

Frequency Resolution

Averaging

Statistics & Probabilities

Statistics & Probabilities Introduction

Mean Value

Standard Deviation

Variance

Skewness

Kurtosis

Probability Distributions Introduction

Normal (Gaussian) Distribution

Central Limit Theorem

Confidence Intervals

Chi-Squared Distribution

Regression Analysis and Least Squares

Rayleigh Distribution

Log-Normal Distribution

Test Control

Random Test Control Parameters

Signal Averaging Dangers

Controlling Random Test Kurtosis

Quiz: Random Testing

Back to: Random Testing

In vibration testing, the power spectral density (PSD) is a powerful analytical tool for understanding and characterizing random vibration. It estimates the distribution of a signal’s strength across a frequency spectrum.

Vibration test engineers can leverage the PSD in various ways to gain insight into the dynamic behavior of the device under test (DUT). Use examples include:

• Estimating stress levels and assessing fatigue life of critical components
• Comparing a test run to a test standard or multiple test runs
• Troubleshooting problems like component failure and assessing root causes
• Identify contributors to vibration energy and their frequency ranges

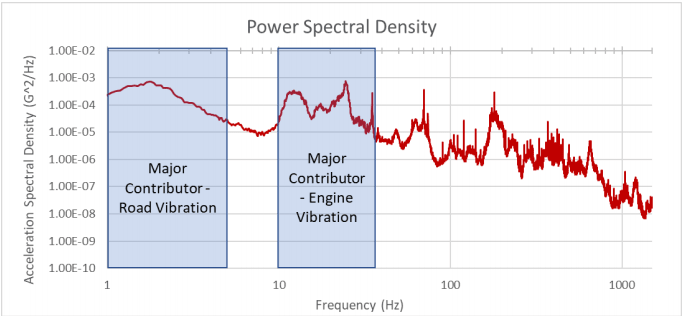
A PSD from transportation data with frequency ranges of known vibration sources.

In this lesson, we will break down the three pivotal elements of the PSD—power, frequency spectra, and density—and discuss the significance of mean-square values, frequency distribution, and normalization to a single hertz bandwidth.

Power, Spectral, & Density

Each word in “power spectral density” represents an essential component of the PSD.

Power: A signal’s mean-square value can represent its magnitude, meaning how far, on average, it strays from zero. The PSD displays a signal’s mean-square amplitude, or “power,” across a frequency spectrum. In this context, “power” refers to the distribution of signal energy over the frequency spectrum rather than a physical quantity, such as watts or horsepower.

Spectral: The PSD is a function of frequency. It represents the distribution of a signal over a accelerometer. The mean-square value is 0.0053G2, and the resonances. Peak amplitudes on a time-domain vibration signal are not as easy to interpret. In Figure 2.4, a cantilever beam was driven at the base by a bandwidths. The squared magnitudes of the spectrum are influenced by the width of the frequency bins. To overcome this variation, the PSD computation divides the squared magnitude by the sample rate to provide a consistent value independent of the frequency bandwidth.

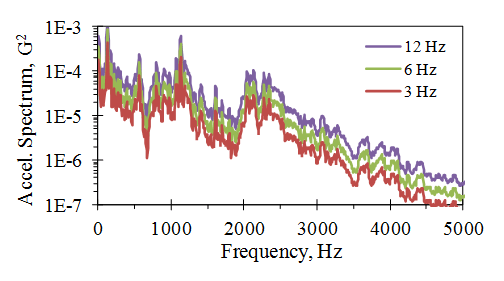
Figure 2.5. Dependence of the frequency spectrum on the frequency bandwidth.

There are cases where individuals confuse the bandwidth-dependent frequency spectrum and the PSD. A bandwidth-normalized magnitude is a feature of the PSD calculation.

Previous Lesson

Random Testing and the Power Spectral Density (PSD)

Next Lesson

How to Compute the PSD