Y=sin^4x+cos^4x - Hàm Số Lượng Giác

Trang chủ » đạo Hàm Sin4x Cos4x » Y=sin^4x+cos^4x - Hàm Số Lượng Giác

Có thể bạn quan tâm

sin^4x+cos^4x

  • A. Tập xác định của hàm số y=sin^4x+cos^4x
  • B. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số y=sin^4x+cos^4x
  • C. Đồ thị hàm số y=sin^4x+cos^4x
  • D. Đạo hàm y=sin^4x+cos^4x
  • E. Giải phương trình lượng giác sin4x; cos4x

Hàm số lượng giác lớp 11 đưa ra phương pháp và các ví dụ cụ thể, giúp các bạn học sinh THPT ôn tập và củng cố kiến thức vềdạng toán lượng giác Toán 11. Tài liệu bao gồm công thức lượng giác, các bài tập ví dụ minh họa có lời giải và bài tập rèn luyện giúp các bạn bao quát nhiều dạng bài chuyên đề lượng giác lớp 11. Chúc các bạn học tập hiệu quả!

A. Tập xác định của hàm số y=sin^4x+cos^4x

Tập xác định của hàm số là: D = \mathbb{R}

B. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số y=sin^4x+cos^4x

Ta có:

y = (sin²x)2 + (cos²x)2

y = sin2x + 2sin²xcos²x + cos2x - 2sin²xcos²x

y = (sin2x + 2sin²xcos²x + cos2x) - 2sin²xcos²x

y = (sin²x + cos²x)² - 2sin²xcos²x

y = 1 - 2sin²xcos²x

y = 1 - \frac{1}{2}{\sin ^2}2x

y = 1 - \frac{1}{4}\left( {1 - \cos 4x} \right)

y = \frac{3}{4} + \frac{1}{4}\cos 4x

Ta có: -1 ≤ cos4x ≤ 1

\begin{matrix} \Rightarrow - \dfrac{1}{4} \leqslant \dfrac{1}{4}\cos 4x \leqslant \dfrac{1}{4} \hfill \\ \Rightarrow \dfrac{3}{4} - \dfrac{1}{4} \leqslant \dfrac{3}{4} + \dfrac{1}{4}\cos 4x \leqslant \dfrac{1}{4} + \dfrac{3}{4} \hfill \\ \Rightarrow \dfrac{1}{2} \leqslant \dfrac{3}{4} + \dfrac{1}{4}\cos 4x \leqslant 1 \hfill \\ \Rightarrow \dfrac{1}{2} \leqslant {\sin ^4}x + {\cos ^4}x \leqslant 1 \hfill \\ \end{matrix}

Giá trị lớn nhất của y = sin^4x+cos^4x là

Giá trị nhỏ nhất của y = sin^4x+cos^4x là 1

C. Đồ thị hàm số y=sin^4x+cos^4x

y=sin^4x+cos^4x

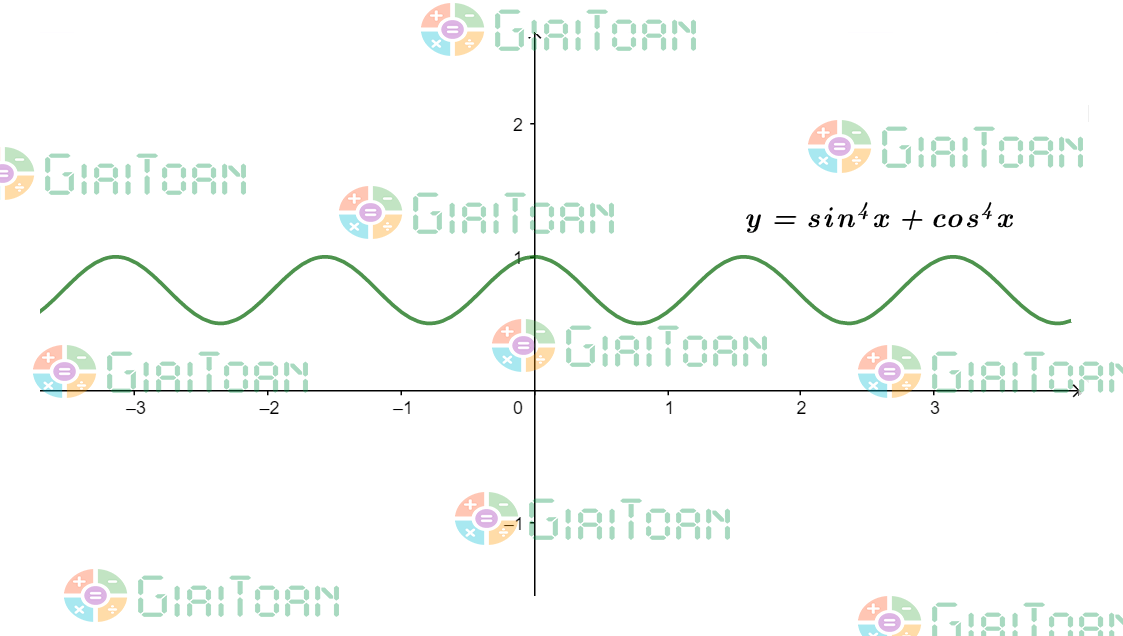
D. Đạo hàm y=sin^4x+cos^4x

y = sin4x+cos4x

=> y’ = (sin4x+cos4x)’

=> y’ = 4sin3x. cosx + 4cos3x . (-sinx)

= 4sin3x. cosx - 4cos3x . sinx

= 4sinx . cosx . (sin3x – cos3x)

= 4sinx . cosx . (sinx – cosx).(sin2x + 3sinx.cosx + cos2x)

= 4sinx . cosx . (sinx – cosx).(1 + 3sinx.cosx)

= 2. sin2x . (sinx – cosx).(1 + 3sinx.cosx)

E. Giải phương trình lượng giác sin4x; cos4x

Ví dụ 1: Giải phương trình:

sinx + sin2x + sin3x + sin4x = cosx + cos2x + cos3x + cos4x

Hướng dẫn giải chi tiết

Ta có:

sin3x – cos3x = (sinx – cosx).(sin2x + cos2x+ sinx.cosx)

sin4x – cos4x = (sin2x – cos2x).(sin2x + cos2x) = - cos2x

Ta biến đổi phương trình như sau:

sinx + sin2x + sin3x + sin4x = cosx + cos2x + cos3x + cos4x

=> sinx – cosx + sin2x – cos2x + sin3x – cos3x + sin4x – cos4x = 0

=> sinx – cosx – cos2x + (sinx – cosx).(sin2x + cos2x+ sinx.cosx) - cos2x = 0

=> sinx – cosx – 2cos2x + (sinx – cosx).(1 + sinx.cosx) = 0

=> (sinx – cosx).[1 + 2(sinx + cosx) + 1 + sinx.cosx] = 0

=> sinx – cosx = 0 hoặc 1 + 2(sinx + cosx) + 1 + sinx.cosx = 0

Trường hợp 1:

sinx – cosx = 0

Giải phương trình ta được x = \frac{\pi }{4} + k\pi ;\left( {k \in \mathbb{Z}} \right)

Trường hợp 2:

1 + 2(sinx + cosx) + 1 + sinx.cosx = 0 (*)

Đặt sinx + cosx = t (điều kiện \left| t \right| \leqslant \sqrt 2)

=> sinx.cosx = \frac{{{t^2} - 1}}{2}

Biến đổi phương trình (*) ta được:

2t + \frac{{{t^2} - 1}}{2} + 2 = 0 \Rightarrow {t^2} + 4t + 3 = 0 \Rightarrow \left[ {\begin{array}{*{20}{c}} {t = - 1} \\ {t = - 3\left( L \right)} \end{array}} \right.

=> sinx + cosx = -1

=> \left[ {\begin{array}{*{20}{c}} {x = \dfrac{{ - \pi }}{2} + k2\pi } \\ {x = \pi + k2\pi } \end{array}\left( {k \in \mathbb{Z}} \right)} \right.

Vậy phương trình có ba họ nghiệm.

Ví dụ 2: Giải phương trình:

sin4x + cos4x + sinx.cosx = 0

Hướng dẫn giải chi tiết

Ta có:

Sinx.cosx = 1/2.sin2x

sin4x + cos4x = 1 - 2sin²xcos²x = 1 – 1/2 .sin22x

Thay vào phương trình ta có:

1 – 1/2 .sin22x+ 1/2.sin2x= 0

=> 2 – sin22x + sin2x = 0

=> sin2x = 2 (loại) hoặc sin2x = -1 (thỏa mãn)

Với sin2x = -1

=> 2x = \frac{{ - \pi }}{2} + k2\pi ;\left( {k \in \mathbb{Z}} \right)

=> x = \frac{{ - \pi }}{4} + k\pi ;\left( {k \in \mathbb{Z}} \right)

Kết luận phương trình có một họ nghiệm

----------------------------------------------------

Hi vọng Các dạng bài tập hàm số lượng giác lớp 11 là tài liệu hữu ích cho các bạn ôn tập kiểm tra năng lực, bổ trợ cho quá trình học tập trong chương trình lớp 11 cũng như ôn luyện cho kì thi THPT Quốc gia. Chúc các bạn học tốt!

Một số tài liệu liên quan:

  • Xét tính chẵn lẻ của hàm số lượng giác
  • Phương trình lượng giác cơ bản
  • Bài toán tính tổng dãy số có quy luật Toán 11
  • Đề khảo sát chất lượng đầu năm lớp 11 môn Toán năm học 2021 - 2022
  • Phương trình lượng giác cơ bản
  • Một người có 7 chiếc áo sơ mi, trong đó có 3 chiếc áo sơ mi trắng; có 5 cà vạt trong đó có 2 cà vạt màu vàng
  • Từ các chữ số 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số tự nhiên lẻ có 6 chữ số đôi một khác nhau
  • Một nhóm học sinh gồm 15 nam và 5 nữ. Người ta muốn chọn từ nhóm ra 5 người để lập thành một đội cờ đỏ
  • Phương trình sinx=-1/2 có bao nhiêu nghiệm thuộc khoảng (-pi; pi)?
  • Phương trình căn 3 sin x cos x = 1 tương đương với phương trình nào sau đây?
  • Tìm tập xác định của hàm số lượng giác
  • Xác định x để ba số 1–x; x^2; 1+x theo thứ tự lập thành một cấp số cộng?
  • Xếp ngẫu nhiên 6 học sinh nam và 2 học sinh nữ thành một hàng ngang
  • Từ các chữ số 1, 2, 3, 4 có thể lập được bao nhiêu số tự nhiên gồm hai chữ số khác nhau?
  • Có bao nhiêu số tự nhiên gồm 6 chữ số khác nhau trong đó có đúng 3 chữ số lẻ và 3 chữ số chẵn?
  • Từ các chữ số 1, 2, 3, 4 có thể lập được bao nhiêu số tự nhiên gồm hai chữ số khác nhau?
  • Một hộp chứa 5 quả cầu đỏ khác nhau và 3 quả cầu xanh khác nhau có bao nhiêu cách chọn ra 2 quả cùng màu?
  • Một nhóm học sinh gồm 15 nam và 5 nữ. Người ta muốn chọn từ nhóm ra 5 người để lập thành một đội cờ đỏ sao cho phải có 1 đội trưởng nam, 1 đội phó nam và có ít nhất 1 nữ. Hỏi có bao nhiêu cách lập đội cờ đỏ.
  • Đội văn nghệ của một trường có 12 học sinh, gồm 5 em học lớp A, 4 em học lớp B và 3 em học lớp C. Cần chọn ra 4 em đi biểu diễn sao cho 4 bạn này thuộc không quá 2 trong 3 lớp trên. Hỏi có bao nhiêu cách chọn như trên?

  • Trong một buổi lao động tình nguyện gồm có 4 học sinh lớp 11A, 5 học sinh lớp 11B và 6 học sinh lớp 11C. Thầy giáo chọn ngẫu nhiên 3 học sinh làm công việc quét dọn.

    a) Có bao nhiêu cách để chọn đủ 3 bạn đến từ 3 lớp khác nhau.

    b) Có bao nhiêu cách chọn để được ít nhất một bạn đến từ lớp 11A.

  • Một lớp học có 33 học sinh, trong đó có 10 học sinh giỏi, 11 học sinh khá và 12 học sinh trung bình. Chọn ngẫu nhiên trong lớp học 4 học sinh đi tham dự trại hè. Tính xác suất để nhóm học sinh được chọn có đủ học sinh giỏi, học sinh khá và học sinh trung bình.

Từ khóa » đạo Hàm Sin4x Cos4x