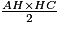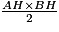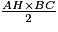Calculer L'aire D'un Triangle - Mathématiques - 5e
Maybe your like
Toggle navigation 5e
L'aire du triangle ABC, en cm2, est égale à :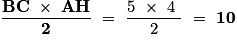 Remarque : on obtient la même aire en calculant :
Remarque : on obtient la même aire en calculant : 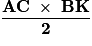 .
.
(AB) est la hauteur relative à [AC] et inversement ;l'aire du triangle ABC est donc égale à :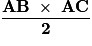 .Remarque : la troisième hauteur (AH) est celle relative à l'hypoténuse [BC] :l'aire du triangle ABC rectangle en A est aussi égale à
.Remarque : la troisième hauteur (AH) est celle relative à l'hypoténuse [BC] :l'aire du triangle ABC rectangle en A est aussi égale à 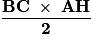 . Exercice n°1
. Exercice n°1
Coche la réponse exacte. L'aire de ce triangle est : Cochez la bonne réponse.
Refaire l'exercice Enlever la correction Montrer la correction Revoir mes derniers choix Toggle Dropdown Pour calculer l'aire de ce triangle, on écrit :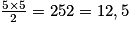 Exercice n°2
Exercice n°2
Coche la réponse exacte. L'aire du triangle ABC est : Cochez la bonne réponse.
Refaire l'exercice Enlever la correction Montrer la correction Revoir mes derniers choix Toggle Dropdown (AH) est la hauteur relative à [BC]. Exercice n°3 Le triangle RST est rectangle en R.RH est la hauteur relative au côté [TS].Les mesures en cm de ses côtés sont ST = 5 ; RS = 3 ; RT = 4. Complète. Écrivez les réponses dans les zones colorées. a. L'aire de RST est de cm2. b. La hauteur RH mesure cm. Refaire l'exercice Enlever la correction Montrer la correction Revoir mes derniers choix Toggle Dropdown a. RST est rectangle en R donc :![]() un partenariat
un partenariat 
 Nos sites / appli Mon espace éducation Cap Concours Il était une histoire Objectif Brevet Apprendre à porter secours La quinte juste Les solutions éducatives MAIF Le fonds MAIF pour l'éducation L'espace enseignant MAIF Informations légales Contact © 2000-2025, Miscellane
Nos sites / appli Mon espace éducation Cap Concours Il était une histoire Objectif Brevet Apprendre à porter secours La quinte juste Les solutions éducatives MAIF Le fonds MAIF pour l'éducation L'espace enseignant MAIF Informations légales Contact © 2000-2025, Miscellane
- Petite section
- Moyenne section
- Grande section
- CP
- CE1
- CE2
- CM1
- CM2
- 6e
- 5e
- 4e
- 3e
- Seconde
- Première
- Première STMG
- Première ST2S
- Terminale
- Terminale STMG
- Terminale STI2D
- Terminale ST2S
- Français
- Mathématiques
- Histoire
- Géographie
- Enseignement moral et civique
- SVT
- Physique-chimie
- Technologie
- Développement durable
- Anglais
- Allemand
- Espagnol
- Révisions Réviser une notion
- Lexique Trouver la définition d'un mot
- Accueil
- Se connecter
- Créer un compte
Aire du triangle quelconque ABC :
(AH) est la hauteur relative à [BC].BC = 5 cm ; AH = 4 cm.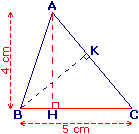 |
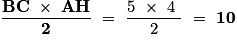 Remarque : on obtient la même aire en calculant :
Remarque : on obtient la même aire en calculant : 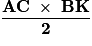 .
.Aire du triangle ABC rectangle en A :
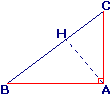 |
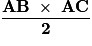 .Remarque : la troisième hauteur (AH) est celle relative à l'hypoténuse [BC] :l'aire du triangle ABC rectangle en A est aussi égale à
.Remarque : la troisième hauteur (AH) est celle relative à l'hypoténuse [BC] :l'aire du triangle ABC rectangle en A est aussi égale à 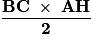 . Exercice n°1
. Exercice n°1 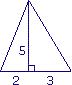 |
| ||
| ||
|
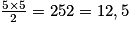 Exercice n°2
Exercice n°2  |
| ||
| ||
|
- aire (RST) = (RS × RT) × 2
- aire (RST) = (4 × 3) × 2 = 6
- aire (RST) = (ST × RH) ÷ 2
- 6 = (5 × RH) ÷ 2

 Nos sites / appli Mon espace éducation Cap Concours Il était une histoire Objectif Brevet Apprendre à porter secours La quinte juste Les solutions éducatives MAIF Le fonds MAIF pour l'éducation L'espace enseignant MAIF Informations légales Contact © 2000-2025, Miscellane
Nos sites / appli Mon espace éducation Cap Concours Il était une histoire Objectif Brevet Apprendre à porter secours La quinte juste Les solutions éducatives MAIF Le fonds MAIF pour l'éducation L'espace enseignant MAIF Informations légales Contact © 2000-2025, Miscellane Tag » Quelle Est L Aire D Un Triangle
-
-
Calculer L'aire D'un Triangle
-
Comment Calculer L'aire D'un Triangle ?
-
L'aire Du Triangle - Maxicours
-
Aire D'un Triangle
-
Démonstration - Formule De L'aire D'un Triangle (vidéo) | Khan Academy
-
Alloprof Aide Aux Devoirs | Alloprof
-
Comment Calculer L’aire D’un Triangle ?
-
Aire D'un Triangle
-
Aire D'un Triangle Rectangle
-
Calcul De L'aire D'un Triangle
-
Comment Calculer L’aire D’un Triangle ?
-
Math - Géométrie : Périmètre & Aire De Triangles
-
Aire Et Surface D'un Triangle Rectangle