Diagonal Matrix - Definition, Inverse - Cuemath

Diagonal Matrix

Before going to learn what is a diagonal matrix, let us recall a few other types of matrices. There are two types of triangular matrices called "lower triangular matrices" and "upper triangular matrices".

• A lower triangular matrix is a square matrix in which all the elements above the principal diagonal are zeros. Example: \(\left[\begin{array}{rr}3 & 0 & 0\\ 2 & 1 & 0\\ 4 & 5 & -3\end{array}\right]\)
• An upper triangular matrix is a square matrix in which all the elements below the principal diagonal are zeros. Example: \(\left[\begin{array}{rr}6 & 1 & 2\\ 0 & 4 & -5\\ 0 & 0 & 7\end{array}\right]\)

A diagonal matrix is a matrix that is both lower triangular and upper triangular? Can you now imagine how a diagonal matrix look like? Let us see.

1.	What is Diagonal Matrix?
2.	Properties of Diagonal Matrix
3.	Determinant of Diagonal Matrix
4.	Inverse of Diagonal Matrix
5.	Diagonalization of a Matrix
6.	FAQs on Diagonal Matrix

What is Diagonal Matrix?

A diagonal matrix is a matrix that is both upper triangular and lower triangular. i.e., all the elements above and below the principal diagonal are zeros and hence the name "diagonal matrix". Its mathematical definition is, a matrix A = [aij] is said to be diagonal if

• A is a square matrix
• aij = 0 when i ≠ j.

Some examples of diagonal matrices are \(\left[\begin{array}{rr}2 & 0 \\ \\ \\ 0 & -3 \end{array}\right]\), \(\left[\begin{array}{rr}3 & 0 & 0\\ 0 & 1 & 0\\ 0 &0 & -6\end{array}\right]\), \(\left[\begin{array}{rr}4 & 0 & 0&0\\ 0 & -2 & 0&0\\ 0 & 0 & 1&0\\0&0&0&7\end{array}\right] \), etc. But can a diagonal matrix have some (or all) of its diagonal elements to be zeros? Yes, it can have as the only condition for it to be a diagonal matrix is concerned with its non-principal diagonal elements (which have to be zeros). In other words, the diagonal elements of a diagonal matrix can be either zeros or non-zeros.

Anti Diagonal Matrix

An anti diagonal matrix is just the mirror image of a diagonal matrix with respect to the placement of the elements. i.e., in an anti-diagonal matrix, all the elements above and below the diagonal (which is NOT the principal diagonal) are zeros. Note that any anti diagonal matrix is a non diagonal matrix.

Examples: \(\left[\begin{array}{rr}0 & 1 \\ \\ \\ 2 & 0 \end{array}\right]\), \(\left[\begin{array}{rr} 0 & 0 & 1\\ 0 & 2 & 0\\ -7 &0 & 0\end{array}\right]\), etc.

Properties of a Diagonal Matrix

Here are the properties of a diagonal matrix based upon its definition.

• Every diagonal matrix is a square matrix.
• Identity matrix, null matrix, and scalar matrix are examples of a diagonal matrix as each of them has its non-principal diagonal elements to be zeros.
• The sum of two diagonal matrices is a diagonal matrix.
• The product of two diagonal matrices (of the same order) is a diagonal matrix where the elements of its principal diagonal are the products of the corresponding elements of the original matrices. Example: For two matrices A = \(\left[\begin{array}{rr}5 & 0 \\ \\ \\ 0 & -2 \end{array}\right]\) and B = \(\left[\begin{array}{rr}7 & 0 \\ \\ \\ 0 & 10 \end{array}\right]\), AB = \(\left[\begin{array}{rr}35 & 0 \\ \\ \\ 0 & -20 \end{array}\right]\)
• Diagonal matrices are commutative under both addition and multiplication. Example: For two matrices A = \(\left[\begin{array}{rr}1 & 0 \\ \\ \\ 0 & -4 \end{array}\right]\) and B = \(\left[\begin{array}{rr}5 & 0 \\ \\ \\ 0 & 8 \end{array}\right]\), A + B = B + A = \(\left[\begin{array}{rr}6 & 0 \\ \\ \\ 0 & 4 \end{array}\right]\) and AB = BA = \(\left[\begin{array}{rr}5 & 0 \\ \\ \\ 0 & -32 \end{array}\right]\)
• Diagonal matrices are symmetric matrices as for any diagonal matrix A, AT = A.

Determinant of Diagonal Matrix

The determinant of a diagonal matrix is the product of its diagonal elements. Let us verify this by taking a 3 x 3 diagonal matrix. Let A = \(\left[\begin{array}{rr}2 & 0 & 0\\ 0 & -3 & 0\\ 0 &0 & 5\end{array}\right]\). We will find its determinant.

det A = 2(-15 - 0) - 0 (0 - 0) + 0 (0 - 0) = -30, which is the product of principal diagonal's elements 2, -3 and 5. Thus,

Thus, a diagonal matrix is a non-singular matrix (whose determinant is not zero) only if all of its principal diagonal elements are non-zeros.

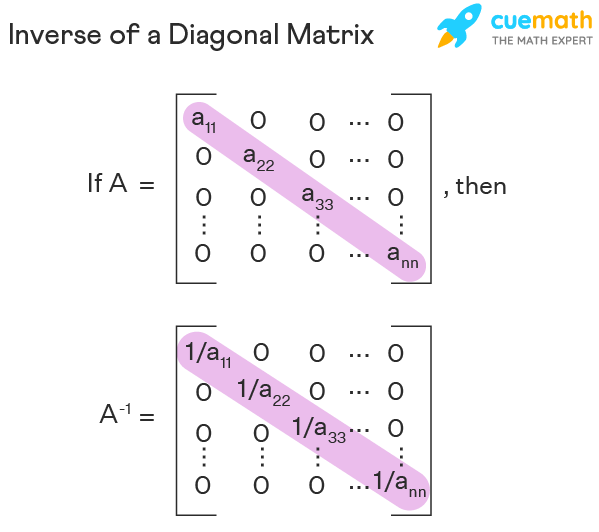
Inverse of Diagonal Matrix

The inverse of a diagonal matrix is a diagonal matrix where the elements of the principal diagonal are the reciprocals of the corresponding elements of the original matrix. Let us verify this by taking a 3 x 3 diagonal matrix. Let A = \(\left[\begin{array}{rr}2 & 0 & 0\\ 0 & -3 & 0\\ 0 &0 & 5\end{array}\right]\). We found (in the previous section) its determinant to be -30. Now we will find its adjoint matrix.

adj A = \(\left[\begin{array}{rr}-15 & 0 & 0\\ 0 & 10 & 0\\ 0 &0 & -6\end{array}\right]\)

We know that the inverse of a matrix A is, A-1 = (adj A) / (det A)

= 1/(-30) \(\left[\begin{array}{rr}-15 & 0 & 0\\ 0 & 10 & 0\\ 0 &0 & -6\end{array}\right]\)

= \(\left[\begin{array}{rr}1/2 & 0 & 0\\ 0 & -1/3 & 0\\ 0 &0 & 1/5\end{array}\right]\)

Here, we can see that A-1 is also a diagonal matrix and its elements in the principal diagonal are the reciprocals of the corresponding elements of A. Thus,

Diagonalization of a Matrix

We study the diagonalization of matrices in linear algebra. Any square matrix A can be written as the product A = XDX-1, where D is a diagonal matrix that is formed by the eigenvalues of A and X is formed by the corresponding eigenvectors of A. i.e., if \(\lambda_1, \lambda_2, ..., \lambda_n\) are the eigenvalues of the matrix A, then

• D = \(\left[\begin{array}{ccccc}\lambda_{1} & 0 & 0 & \ldots & 0 \\ 0 &\lambda_{2} & 0 & \ldots & 0 \\ 0 & 0 & \lambda_{3} & \ldots & 0 \\ \vdots & \vdots & \vdots & & \vdots \\ 0 & 0 & 0 & \ldots & \lambda_{n}\end{array}\right]\)
• X = \(\left[\begin{array}{llll}\overrightarrow{ {x_1}} & {\overrightarrow{ {x}}}_{ {2}} & \ldots & {\overrightarrow{ {x}}}_{ {n}}\end{array}\right]\), where \(\overrightarrow{ {x_1}}, \overrightarrow{ {x_2}}, ..., \overrightarrow{ {x_n}}\) are the eigenvectors correspoding to the eigenvalues \(\lambda_1, \lambda_2, ..., \lambda_n\) in order and are written as column vectors.

We can see an example of diagonalizing a matrix in the "Solved Examples" section below.

Important Notes on Diagonal Matrix:

• In a diagonal matrix, all the elements except the elements in the principal diagonal are zeros.
• Hence, the determinant of a diagonal matrix is the product of the elements of the principal diagonal.
• The inverse of a diagonal matrix is also a diagonal matrix in which the elements of the principal diagonal are the reciprocals of the elements of the principal diagonal matrix of the original matrix.
• Any diagonal matrix is symmetric.

☛ Related Topics:

• Diagonal Matrix Calculator
• Matrix Addition Calculator
• Matrix Multiplication Calculator
• Matrix Formula