How To Diagonalize A Matrix. Step By Step Explanation.

Maybe your like

Problem 211

In this post, we explain how to diagonalize a matrix if it is diagonalizable.

As an example, we solve the following problem.

Diagonalize the matrix \[A=\begin{bmatrix} 4 & -3 & -3 \\ 3 &-2 &-3 \\ -1 & 1 & 2 \end{bmatrix}\] by finding a nonsingular matrix $S$ and a diagonal matrix $D$ such that $S^{-1}AS=D$.

(Update 10/15/2017. A new example problem was added.) Add to solve later

Diagonalization Procedure

Let $A$ be the $n\times n$ matrix that you want to diagonalize (if possible).

Find the characteristic polynomial $p(t)$ of $A$.
Find eigenvalues $\lambda$ of the matrix $A$ and their algebraic multiplicities from the characteristic polynomial $p(t)$.
For each eigenvalue $\lambda$ of $A$, find a basis of the eigenspace $E_{\lambda}$. If there is an eigenvalue $\lambda$ such that the geometric multiplicity of $\lambda$, $\dim(E_{\lambda})$, is less than the algebraic multiplicity of $\lambda$, then the matrix $A$ is not diagonalizable. If not, $A$ is diagonalizable, and proceed to the next step.
If we combine all basis vectors for all eigenspaces, we obtained $n$ linearly independent eigenvectors $\mathbf{v}_1, \mathbf{v}_2, \dots, \mathbf{v}_n$.
Define the nonsingular matrix \[S=[\mathbf{v}_1 \mathbf{v}_2 \dots \mathbf{v}_n] .\]
Define the diagonal matrix $D$, whose $(i,i)$-entry is the eigenvalue $\lambda$ such that the $i$-th column vector $\mathbf{v}_i$ is in the eigenspace $E_{\lambda}$.
Then the matrix $A$ is diagonalized as \[ S^{-1}AS=D.\]

Example of a matrix diagonalization

Now let us examine these steps with an example. Let us consider the following $3\times 3$ matrix. \[A=\begin{bmatrix} 4 & -3 & -3 \\ 3 &-2 &-3 \\ -1 & 1 & 2 \end{bmatrix}.\] We want to diagonalize the matrix if possible.

Step 1: Find the characteristic polynomial

The characteristic polynomial $p(t)$ of $A$ is \[p(t)=\det(A-tI)=\begin{vmatrix} 4-t & -3 & -3 \\ 3 &-2-t &-3 \\ -1 & 1 & 2-t \end{vmatrix}.\] Using the cofactor expansion, we get \[p(t)=-(t-1)^2(t-2).\]

Step 2: Find the eigenvalues

From the characteristic polynomial obtained in Step 1, we see that eigenvalues are \[\lambda=1 \text{ with algebraic multiplicity } 2\] and \[\lambda=2 \text{ with algebraic multiplicity } 1.\]

Step 3: Find the eigenspaces

Let us first find the eigenspace $E_1$ corresponding to the eigenvalue $\lambda=1$. By definition, $E_1$ is the null space of the matrix \[A-I=\begin{bmatrix} 3 & -3 & -3 \\ 3 &-3 &-3 \\ -1 & 1 & 1 \end{bmatrix} \rightarrow \begin{bmatrix} 1 & -1 & -1 \\ 0 &0 &0 \\ 0 & 0 & 0 \end{bmatrix}\] by elementary row operations. Hence if $(A-I)\mathbf{x}=\mathbf{0}$ for $\mathbf{x}\in \R^3$, we have \[x_1=x_2+x_3.\] Therefore, we have \begin{align*} E_1=\calN(A-I)=\left \{\quad \mathbf{x}\in \R^3 \quad \middle| \quad \mathbf{x}=x_2\begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix}+x_3\begin{bmatrix} 1 \\ 0 \\ 1 \end{bmatrix} \quad \right \}. \end{align*} From this, we see that the set \[\left\{\quad\begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix},\quad \begin{bmatrix} 1 \\ 0 \\ 1 \end{bmatrix}\quad \right\}\] is a basis for the eigenspace $E_1$. Thus, the dimension of $E_1$, which is the geometric multiplicity of $\lambda=1$, is $2$.

Similarly, we find a basis of the eigenspace $E_2=\calN(A-2I)$ for the eigenvalue $\lambda=2$. We have \begin{align*} A-2I=\begin{bmatrix} 2 & -3 & -3 \\ 3 &-4 &-3 \\ -1 & 1 & 0 \end{bmatrix} \rightarrow \cdots \rightarrow \begin{bmatrix} 1 & 0 & 3 \\ 0 &1 &3 \\ 0 & 0 & 0 \end{bmatrix} \end{align*} by elementary row operations. Then if $(A-2I)\mathbf{x}=\mathbf{0}$ for $\mathbf{x}\in \R^3$, then we have \[x_1=-3x_3 \text{ and } x_2=-3x_3.\] Therefore we obtain \begin{align*} E_2=\calN(A-2I)=\left \{\quad \mathbf{x}\in \R^3 \quad \middle| \quad \mathbf{x}=x_3\begin{bmatrix} -3 \\ -3 \\ 1 \end{bmatrix} \quad \right \}. \end{align*} From this we see that the set \[\left \{ \quad \begin{bmatrix} -3 \\ -3 \\ 1 \end{bmatrix} \quad \right \}\] is a basis for the eigenspace $E_2$ and the geometric multiplicity is $1$.

Since for both eigenvalues, the geometric multiplicity is equal to the algebraic multiplicity, the matrix $A$ is not defective, and hence diagonalizable.

Step 4: Determine linearly independent eigenvectors

From Step 3, the vectors \[\mathbf{v}_1=\begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix}, \mathbf{v}_2=\begin{bmatrix} 1 \\ 0 \\ 1 \end{bmatrix}, \mathbf{v}_3=\begin{bmatrix} -3 \\ -3 \\ 1 \end{bmatrix} \] are linearly independent eigenvectors.

Step 5: Define the invertible matrix $S$

Define the matrix $S=[\mathbf{v}_1 \mathbf{v}_2 \mathbf{v}_3]$. Thus we have \[S=\begin{bmatrix} 1 & 1 & -3 \\ 1 &0 &-3 \\ 0 & 1 & 1 \end{bmatrix}\] and the matrix $S$ is nonsingular (since the column vectors are linearly independent).

Step 6: Define the diagonal matrix $D$

Define the diagonal matrix \[D=\begin{bmatrix} 1 & 0 & 0 \\ 0 &1 &0 \\ 0 & 0 & 2 \end{bmatrix}.\] Note that $(1,1)$-entry of $D$ is $1$ because the first column vector $\mathbf{v}_1=\begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix}$ of $S$ is in the eigenspace $E_1$, that is, $\mathbf{v}_1$ is an eigenvector corresponding to eigenvalue $\lambda=1$. Similarly, the $(2,2)$-entry of $D$ is $1$ because the second column $\mathbf{v}_2=\begin{bmatrix} 1 \\ 0 \\ 1 \end{bmatrix}$ of $S$ is in $E_1$. The $(3,3)$-entry of $D$ is $2$ because the third column vector $\mathbf{v}_3=\begin{bmatrix} -3 \\ -3 \\ 1 \end{bmatrix}$ of $S$ is in $E_2$.

(The order you arrange the vectors $\mathbf{v}_1, \mathbf{v_2}, \mathbf{v}_3$ to form $S$ does not matter but once you made $S$, then the order of the diagonal entries is determined by $S$, that is, the order of eigenvectors in $S$.)

Step 7: Finish the diagonalization

Finally, we can diagonalize the matrix $A$ as \[S^{-1}AS=D,\] where \[S=\begin{bmatrix} 1 & 1 & -3 \\ 1 &0 &-3 \\ 0 & 1 & 1 \end{bmatrix} \text{ and } D=\begin{bmatrix} 1 & 0 & 0 \\ 0 &1 &0 \\ 0 & 0 & 2 \end{bmatrix}.\] (Here you don’t have to find the inverse matrix $S^{-1}$ unless you are asked to do so.)

Diagonalization Problems and Examples

Check out the following problems about the diagonalization of a matrix to see if you understand the procedure.

Problem. Diagonalize \[A=\begin{bmatrix} 1 & 2\\ 4& 3 \end{bmatrix}\] and compute $A^{100}$.

For a solution of this problem and related questions, see the post “Diagonalize a 2 by 2 Matrix $A$ and Calculate the Power $A^{100}$“.

Problem. Determine whether the matrix \[A=\begin{bmatrix} 0 & 1 & 0 \\ -1 &0 &0 \\ 0 & 0 & 2 \end{bmatrix}\] is diagonalizable. If it is diagonalizable, then find the invertible matrix $S$ and a diagonal matrix $D$ such that $S^{-1}AS=D$.

For a solution, check out the post “Diagonalize the 3 by 3 Matrix if it is Diagonalizable“.

Problem. Let \[A=\begin{bmatrix} 2 & -1 & -1 \\ -1 &2 &-1 \\ -1 & -1 & 2 \end{bmatrix}.\] Determine whether the matrix $A$ is diagonalizable. If it is diagonalizable, then diagonalize $A$.

For a solution, see the post “Quiz 13 (Part 1) Diagonalize a matrix.“.

Problem. Diagonalize the matrix \[A=\begin{bmatrix} 1 & 1 & 1 \\ 1 &1 &1 \\ 1 & 1 & 1 \end{bmatrix}.\]

In the solution given in the post “Diagonalize the 3 by 3 Matrix Whose Entries are All One“, we use an indirect method to find eigenvalues and eigenvectors.

The next problem is a diagonalization problem of a matrix with variables.

Problem. Diagonalize the complex matrix \[A=\begin{bmatrix} a & b-a\\ 0& b \end{bmatrix}.\] Using the result of the diagonalization, compute $A^k$ for each $k\in \N$.

The solution is given in the post↴ Diagonalize the Upper Triangular Matrix and Find the Power of the Matrix

A Hermitian Matrix can be diagonalized by a unitary matrix

Theorem. If $A$ is a Hermitian matrix, then $A$ can be diagonalized by a unitary matrix $U$.

This means that there exists a unitary matrix $U$ such that $U^{-1}AU$ is a diagonal matrix.

Problem. Diagonalize the Hermitian matrix \[A=\begin{bmatrix} 1 & i\\ -i& 1 \end{bmatrix}\] by a unitary matrix.

The solution is given in the post ↴ Diagonalize the $2\times 2$ Hermitian Matrix by a Unitary Matrix

More from my site

Quiz 13 (Part 1) Diagonalize a Matrix Let \[A=\begin{bmatrix} 2 & -1 & -1 \\ -1 &2 &-1 \\ -1 & -1 & 2 \end{bmatrix}.\] Determine whether the matrix $A$ is diagonalizable. If it is diagonalizable, then diagonalize $A$. That is, find a nonsingular matrix $S$ and a diagonal matrix $D$ such that […]
Two Matrices with the Same Characteristic Polynomial. Diagonalize if Possible. Let \[A=\begin{bmatrix} 1 & 3 & 3 \\ -3 &-5 &-3 \\ 3 & 3 & 1 \end{bmatrix} \text{ and } B=\begin{bmatrix} 2 & 4 & 3 \\ -4 &-6 &-3 \\ 3 & 3 & 1 \end{bmatrix}.\] For this problem, you may use the fact that both matrices have the same characteristic […]
True or False. Every Diagonalizable Matrix is Invertible Is every diagonalizable matrix invertible? Solution. The answer is No. Counterexample We give a counterexample. Consider the $2\times 2$ zero matrix. The zero matrix is a diagonal matrix, and thus it is diagonalizable. However, the zero matrix is not […]
Maximize the Dimension of the Null Space of $A-aI$ Let \[ A=\begin{bmatrix} 5 & 2 & -1 \\ 2 &2 &2 \\ -1 & 2 & 5 \end{bmatrix}.\] Pick your favorite number $a$. Find the dimension of the null space of the matrix $A-aI$, where $I$ is the $3\times 3$ identity matrix. Your score of this problem is equal to that […]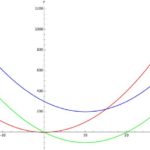
Given Graphs of Characteristic Polynomial of Diagonalizable Matrices, Determine the Rank of Matrices Let $A, B, C$ are $2\times 2$ diagonalizable matrices. The graphs of characteristic polynomials of $A, B, C$ are shown below. The red graph is for $A$, the blue one for $B$, and the green one for $C$. From this information, determine the rank of the matrices $A, B,$ and […]
Determine Dimensions of Eigenspaces From Characteristic Polynomial of Diagonalizable Matrix Let $A$ be an $n\times n$ matrix with the characteristic polynomial \[p(t)=t^3(t-1)^2(t-2)^5(t+2)^4.\] Assume that the matrix $A$ is diagonalizable. (a) Find the size of the matrix $A$. (b) Find the dimension of the eigenspace $E_2$ corresponding to the eigenvalue […]
Determine Eigenvalues, Eigenvectors, Diagonalizable From a Partial Information of a Matrix Suppose the following information is known about a $3\times 3$ matrix $A$. \[A\begin{bmatrix} 1 \\ 2 \\ 1 \end{bmatrix}=6\begin{bmatrix} 1 \\ 2 \\ 1 \end{bmatrix}, \quad A\begin{bmatrix} 1 \\ -1 \\ 1 […]
Quiz 12. Find Eigenvalues and their Algebraic and Geometric Multiplicities (a) Let \[A=\begin{bmatrix} 0 & 0 & 0 & 0 \\ 1 &1 & 1 & 1 \\ 0 & 0 & 0 & 0 \\ 1 & 1 & 1 & 1 \end{bmatrix}.\] Find the eigenvalues of the matrix $A$. Also give the algebraic multiplicity of each eigenvalue. (b) Let \[A=\begin{bmatrix} 0 & 0 & 0 & 0 […]