Inverse Function - Definition, Formula, Graph, Examples - Cuemath

Inverse Function

Inverse function is represented by f-1 with regards to the original function f and the domain of the original function becomes the range of inverse function and the range of the given function becomes the domain of the inverse function. The graph of the inverse function is obtained by swapping (x, y) with (y, x) with reference to the line y = x.

Let us learn more about the inverse function, the steps to find the inverse function, and the graph of inverse function.

1.	What Is Inverse Function?
2.	Steps to Find An Inverse Function
3.	Graph of An Inverse Function
4.	Examples of Inverse Function
5.	Practice Questions on Inverse Function
6.	FAQs on Inverse Function

What Is Inverse Function?

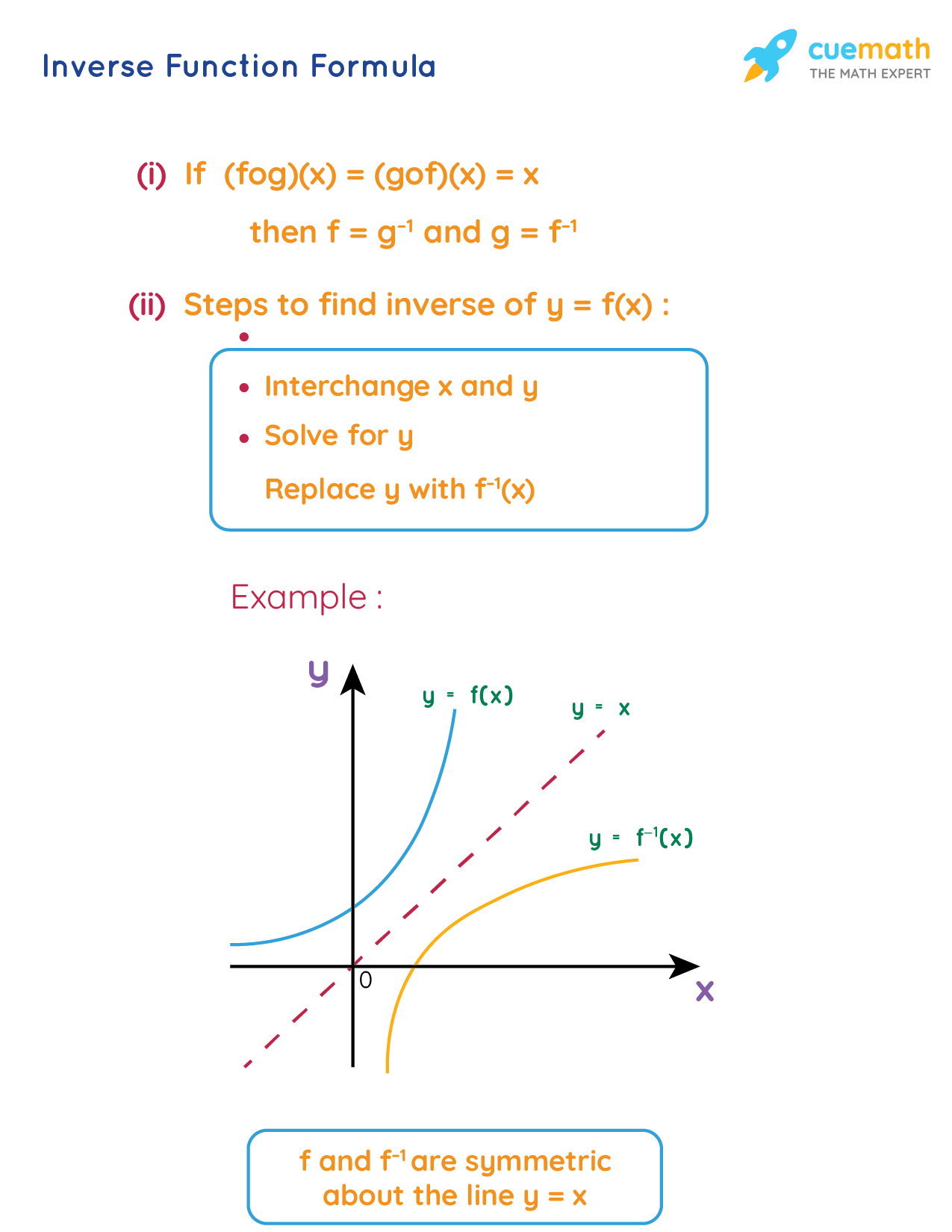
The inverse of a function f is denoted by f-1 and it exists only when f is both one-one and onto function. Note that f-1 is NOT the reciprocal of f. The composition of the function f and the reciprocal function f-1 gives the domain value of x.

(f o f-1) (x) = (f-1 o f) (x) = x

For a function 'f' to be considered an inverse function, each element in the range y ∈ Y has been mapped from some element x ∈ X in the domain set, and such a relation is called a one-one relation or an injunction relation. Also the inverse f-1 of the given function has a domain y ∈ Y is related to a distinct element x ∈ X in the codomain set, and this kind of relationship with reference to the given function 'f' is an onto function or a surjection function. Thus the inverse function being an injunctive and a surjection function, is called a bijective function.

Let us consider a function f whose domain is the set X and the codomain is the set Y. The function f is invertible if there exists another function g whose domain is Y and its codomain is X. These two functions can be represented as f(x) = Y, and g(y) = X. For this situation, if the function f(x) is inverse, then its inverse function g(x) is unique.

If the composition of two functions f(x), and g(x), results in an identity function f(g(x))= x, then the two functions are said to be inverses of each other. If the application of a function to x as input gives n output of y, then the application of another function g to y should give back the value of x. Hence the inverse of a function reverses the function. The domain of the given function becomes the range of the inverse function, and the range of the given function becomes the domain of the inverse function.

Steps To Find An Inverse Function

The following sequence of steps would help in conveniently finding the inverse of a function. Here we consider a function f(x) = ax + b, and aim at finding the inverse of this function through the following steps.

• For the given function f(x) = ax + b, replace f(x) = y, to obtain y = ax + b.
• Interchange the x with y and the y with x in the function y = ax + b to obtain x = ay + b.
• Here solve the expression x = ay + b for y. And we obtain y = (x - b/a
• Finlly replace y = f-1(x), and we have f-1(x) = (x - b)/a.

Graph of An Inverse Function

The injective function is the reflection of the origin function with reference to the line y = x, and is obtained by swapping (x, y) with the (y, x).

If the graphs of two functions are given, we can identify whether they are inverses of each other. If the graphs of both functions are symmetric with respect to the line y = x, then we say that the two functions are inverses of each other. This is because of the fact that if (x, y) lies on the function, then (y, x) lies on its inverse function.

Related Topics

The following topics help in a better understanding of inverse function.

• Bijective Function
• Injective Function
• Periodic Function
• Continuous Function
• Signum Function
• Relations and Functions