Inverse Function: Rule, Domain, Range, Graph

• Tuition
  • Tuition Centre
  • Testimonials & Results
• A Maths
  • O Level Solutions
  • Textbook Solutions
  • Formulas
  • Revision Notes
  • Unsubscribe (For Members)
• E Maths
  • O Level Solutions
  • Sec 3 Textbook Solutions
  • Sec 4 Textbook Solutions
  • Formulas
  • Unsubscribe (For Members)
• Contact

Menu

H2 Maths Formulas, Techniques & Graphs >> Functions and Graphs >> Functions >>

Inverse function: Rule, Domain, Rule & Graph

The inverse of a function exist only if the function is a 1-1 function.

Example

$$ g : x \mapsto x^2 - 2x - 2, \phantom{000} x \in \mathbb{R}, 1 \le x \le 4 $$

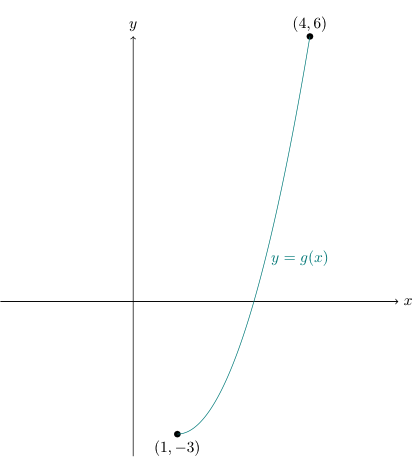
$g$ is a 1-1 function and $$ D_g = [1, 4], R_g = [-3, 6] $$

Domain & Range

The domain and range of $f$ and its inverse $f^{-1}$ are related by: $$ \boxed{ D_f = R_{f^{-1}} } $$ $$ \boxed{ R_f = D_{f^{-1}} } $$

Example

$$ g : x \mapsto x^2 - 2x - 2, \phantom{000} x \in \mathbb{R}, 1 \le x \le 4 $$

and $$ D_g = [1, 4] \text{ and } R_g = [-3, 6] $$

Since the inverse function ‘reverses’ the original function, $$ D_{g^{-1}} = R_g = [-3, 6] $$ $$ R_{g^{-1}} = D_g = [1, 4] $$

Rule of inverse function

Steps:

1. Let y equals to rule of function, i.e y = f(x)

2. Make x the subject of the equation (and if applicable, reject any inappropriate expression)

3. Form f⁻¹ by replacing y with x

Example

$$ g : x \mapsto x^2 - 2x - 2, \phantom{000} x \in \mathbb{R}, 1 \le x \le 4 $$

Step 1: Let y = g(x): $$ y = x^2 - 2x - 2 $$

Step 2: Make x the subject and reject the inappropriate expression given $D_g = [1 , 4]$ \begin{align} y + 2 & = x^2 - 2x \\ y + 2 & = \left(x - {2 \over 2}\right)^2 - \left(2 \over 2\right)^2 \\ y + 2 & = (x - 1)^2 - (1)^2 \\ y + 2 & = (x - 1)^2 - 1 \\ y + 3 & = (x - 1)^2 \\ \pm \sqrt{y + 3} & = x - 1 \\ 1 \pm \sqrt{y + 3} & = x \\ \\ \text{Since } & D_f = [1, 4], \\ x & = 1 + \sqrt{y + 3} \end{align}

Step 3: Form g-1 by replacing y with x $$ g^{-1} : x \mapsto 1 + \sqrt{x + 3}, \phantom{000} x \in \mathbb{R}, -3 \le x \le 6 $$

Graph of inverse function

The graph of a function and its inverse function are reflections about the line y = x.

Example

Given $$ g : x \mapsto x^2 - 2x - 2, \phantom{000} x \in \mathbb{R}, 1 \le x \le 4 $$

and $$ D_g = [1, 4] \text{ and } R_g = [-3, 6] $$

To obtain the graph of the inverse function by ‘DrawInv’ function in GC:

More on Functions:

• Functions

  • Test for function - Vertical line test

  • Find range of function by GC

• Inverse function

  • Rule, domain, range & graph of inverse functions

• Composite functions

  • Conditions for composite function to exist

  • Find the range of composite function

• Other concepts (on Functions)

  • Composite functions f⁻¹f and ff⁻¹

  • Self-inverse functions

Other formulas, techniques & graphs