3.5 Graphing Functions Using Stretches And Compressions

" Skip to content

Adding a constant to the inputs or outputs of a function changed the position of a graph with respect to the axes, but it did not affect the shape of a graph. We now explore the effects of multiplying the inputs or outputs by some quantity.

We can transform the inside (input values) of a function or we can transform the outside (output values) of a function. Each change has a specific effect that can be seen graphically.

Vertical Stretches and Compressions

When we multiply a function by a positive constant, we get a function whose graph is stretched or compressed vertically in relation to the graph of the original function. If the constant is greater than 1, we get a vertical stretch; if the constant is between 0 and 1, we get a vertical compression. Figure 3-13 shows a function multiplied by constant factors 2 and 0.5 and the resulting vertical stretch and compression.

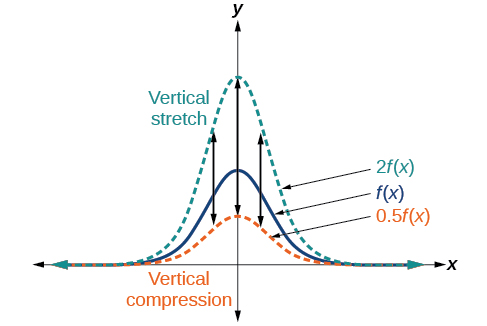
Vertical Stretches and Compressions

Given a function [latex]\text{}f\left(x\right),\text{}[/latex] a new function [latex]\text{}g\left(x\right)=af\left(x\right),\text{}[/latex] where [latex]\text{}a\text{}[/latex] is a constant, is a vertical stretch or vertical compression of the function [latex]\text{}f\left(x\right)[/latex].

• If [latex]\text{}a>1\text{}[/latex], then the graph will be stretched.
• If [latex]\text{}0 < a1\text{}[/latex], then the graph will be compressed by [latex]\text{}\frac{1}{b}[/latex].
• If [latex]\text{}0 < b < 1\text{}[/latex], then the graph will be stretched by [latex]\text{}\frac{1}{b}[/latex].
• If [latex]\text{}b1\text{}[/latex] for a compression or [latex]\text{}0 < b < 1\text{}[/latex] for a stretch.

Suppose a scientist is comparing a population of fruit flies to a population that progresses through its lifespan twice as fast as the original population. In other words, this new population, [latex]\text{}R\text{}[/latex], will progress in 1 hour the same amount as the original population does in 2 hours, and in 2 hours, it will progress as much as the original population does in 4 hours. Sketch a graph of this population.

Analysis

Note that the effect on the graph is a horizontal compression where all input values are half of their original distance from the vertical axis.

Solution

A function [latex]\text{}f\left(x\right)\text{}[/latex] is given as Table 7. Create a table for the function [latex]\text{}g\left(x\right)=f\left(\frac{1}{2}x\right)[/latex].

Table 7

[latex]x[/latex]	2	4	6	8
[latex]f\left(x\right)[/latex]	1	3	7	11

Analysis

Because each input value has been doubled, the result is that the function [latex]\text{}g\left(x\right)\text{}[/latex] has been stretched horizontally by a factor of 2.

Solution

Relate the function [latex]\text{}g\left(x\right)\text{}[/latex] to [latex]\text{}f\left(x\right)\text{}[/latex] in Figure 3-17.



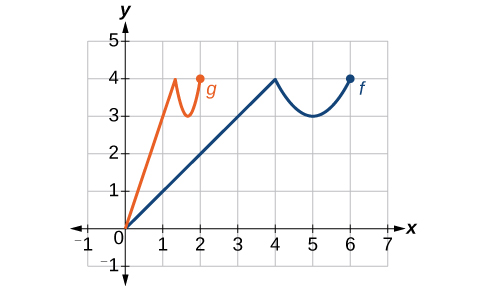
Analysis

Notice that the coefficient needed for a horizontal stretch or compression is the reciprocal of the stretch or compression. So to stretch the graph horizontally by a scale factor of 4, we need a coefficient of [latex]\text{}\frac{1}{4}\text{}[/latex] in our function: [latex]\text{}f\left(\frac{1}{4}x\right)\text{}[/latex]. This means that the input values must be four times larger to produce the same result, requiring the input to be larger, causing the horizontal stretching.

Solution

Write a formula for the toolkit square root function horizontally stretched by a factor of 3.

Solution

Performing a Sequence of Transformations

When combining transformations, it is very important to consider the order of the transformations. For example, vertically shifting by 3 and then vertically stretching by 2 does not create the same graph as vertically stretching by 2 and then vertically shifting by 3, because when we shift first, both the original function and the shift get stretched, while only the original function gets stretched when we stretch first.

When we see an expression such as [latex]\text{}\text{}2f\left(x\right)+3\text{}[/latex], which transformation should we start with? The answer here follows nicely from the order of operations. Given the output value of [latex]\text{}f\left(x\right)\text{}[/latex], we first multiply by 2, causing the vertical stretch, and then add 3, causing the vertical shift. In other words, multiplication before addition.

Horizontal transformations are a little trickier to think about. When we write [latex]\text{}g\left(x\right)=f\left(2x+3\right)\text{}[/latex], for example, we have to think about how the inputs to the function [latex]\text{}g\text{}[/latex] relate to the inputs to the function [latex]\text{}\text{}f\text{}[/latex]. Suppose we know [latex]\text{}f\left(7\right)=12\text{}[/latex]. What input to [latex]\text{}g\text{}[/latex] would produce that output? In other words, what value of [latex]\text{}x\text{}[/latex] will allow [latex]\text{}g\left(x\right)=f\left(2x+3\right)=12\text{}[/latex]? We would need [latex]\text{}2x+3=7\text{}[/latex]. To solve for [latex]\text{}x\text{}[/latex], we would first subtract 3, resulting in a horizontal shift, and then divide by 2, causing a horizontal compression.

This format ends up being very difficult to work with, because it is usually much easier to horizontally stretch a graph before shifting. We can work around this by factoring inside the function.

[latex]f\left(bx+p\right)=f\left(b\left(x+\frac{p}{b}\right)\right)[/latex]

Let’s work through an example.

[latex]f\left(x\right)={\left(2x+4\right)}^{2}[/latex]

We can factor out a 2.

[latex]f\left(x\right)={\left(2\left(x+2\right)\right)}^{2}[/latex]

Now we can more clearly observe a horizontal shift to the left 2 units and a horizontal compression. Factoring in this way allows us to horizontally stretch first and then shift horizontally.

Combining Transformations

When combining vertical transformations written in the form [latex]\text{}af\left(x\right)+k,\text{}[/latex] first vertically stretch by [latex]\text{}a\text{}[/latex] and then vertically shift by [latex]\text{}k[/latex].

When combining horizontal transformations written in the form [latex]\text{}f\left(bx-h\right)\text{}[/latex], first horizontally shift by [latex]\text{}h\text{}[/latex] and then horizontally stretch by [latex]\text{}\frac{1}{b}[/latex].

When combining horizontal transformations written in the form [latex]\text{}f\left(b\left(x-h\right)\right)\text{}[/latex], first horizontally stretch by [latex]\text{}\frac{1}{b}\text{}[/latex] and then horizontally shift by [latex]\text{}h[/latex].

Horizontal and vertical transformations are independent. It does not matter whether horizontal or vertical transformations are performed first.

Given Table 8 for the function [latex]\text{}f\left(x\right)\text{}[/latex], create a table of values for the function [latex]\text{}g\left(x\right)=2f\left(3x\right)+1[/latex].

Table 8

[latex]x[/latex]	6	12	18	24
[latex]f\left(x\right)[/latex]	10	14	15	17

Solution

Use the graph of [latex]\text{}f\left(x\right)\text{}[/latex] in Figure 3-18 to sketch a graph of [latex]\text{}k\left(x\right)=f\left(\frac{1}{2}x+1\right)-3[/latex].



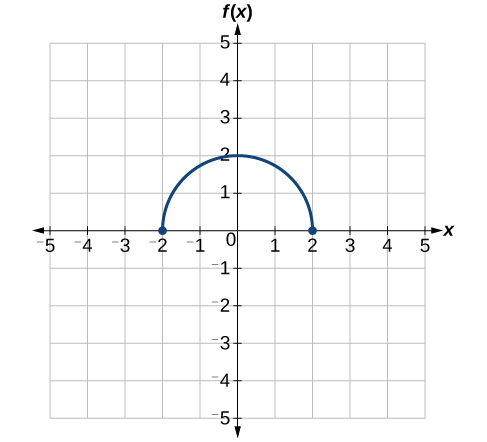
Solution

Access for free at https://openstax.org/books/precalculus/pages/1-introduction-to-functions

Previous/next navigation

Previous: 3.4 Determining Even and Odd Functions Next: 3.6 Review and Summary Back to top

License



Math 3080 Preparation Copyright © 2022 by Erin Kox is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book

Share on X Share on LinkedIn Share via Email