How To Vertically Transform Parent Graphs Article

X-Men For Dummies is here and we're hosting the ultimate holiday giveaway to celebrate! Enter now for your chance to win. Dummies AI Browse Book & Article Categories

Book & Article Categories

closeTechnologyAcademics & The ArtsHome, Auto, & HobbiesBody, Mind, & SpiritBusiness, Careers, & MoneyCollections

Collections

Explore all collectionscloseBYOB (Be Your Own Boss)Be a Rad DadCareer ShiftingContemplating the CosmosFor Those Seeking Peace of MindFor the Aspiring AficionadoFor the Budding Cannabis EnthusiastFor the College BoundFor the Exam-Season CrammerFor the Game Day PrepperCustom Solutions

• Book & Article Categories
• Collections
• Custom Solutions
• Dummies AI

• Main Menu

• Book & Article Categories

• Technology
• Academics & The Arts
• Home, Auto, & Hobbies
• Body, Mind, & Spirit
• Business, Careers, & Money
• Dummies AI

• Main Menu

• Book & Article Categories

• Technology
• Academics & The Arts
• Home, Auto, & Hobbies
• Body, Mind, & Spirit
• Business, Careers, & Money
• Dummies AI

• Main Menu

• Collections

  Explore all collections

• BYOB (Be Your Own Boss)
• Be a Rad Dad
• Career Shifting
• Contemplating the Cosmos
• For Those Seeking Peace of Mind
• For the Aspiring Aficionado
• For the Budding Cannabis Enthusiast
• For the College Bound
• For the Exam-Season Crammer
• For the Game Day Prepper
• Dummies AI

HomeAcademics & The Arts ArticlesMath ArticlesPre-Calculus ArticlesHow to Vertically Transform Parent GraphsByYang Kuang Elleyne Kase Updated2016-03-26 15:24:16From the bookNo items found.Share

• 
• 
• 
• 
• 

Download E-BookPersonal Finance For DummiesExplore BookPre-Calculus All-in-One For Dummies Explore BookBuy NowBuy on AmazonBuy on WileySubscribe on PerlegoDownload E-BookPersonal Finance For DummiesExplore BookPre-Calculus All-in-One For DummiesExplore BookBuy NowBuy on AmazonBuy on WileySubscribe on Perlego

When you apply a vertical transformation to a parent graph, you are stretching or shrinking the graph along the y-axis, which changes its height. A number (or coefficient) multiplying in front of a function causes the vertical transformation. The coefficient always affects the height of each and every point in the graph of the function. We call the vertical transformation a stretch if the coefficient is greater than 1 and a shrink if the coefficient is between 0 and 1.

For example, the graph of f(x) = 2x2 takes the graph of f(x) = x2 and stretches it by a vertical factor of two. That means that each time you plot a point vertically on the graph, the value gets multiplied by two (making the graph twice as tall at each point). For example, in f(x)=x2, 1 gets mapped to 2×12=2, 2 gets mapped to 2×22=8, 3 gets mapped to 2×32=18, etc.

The vertical transformation of f(x) = 2x2 and

are shown in this figure.

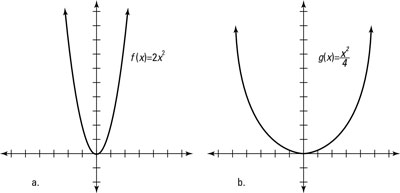
The transformationrules apply to any function, so the vertical transformation of

is shown here.

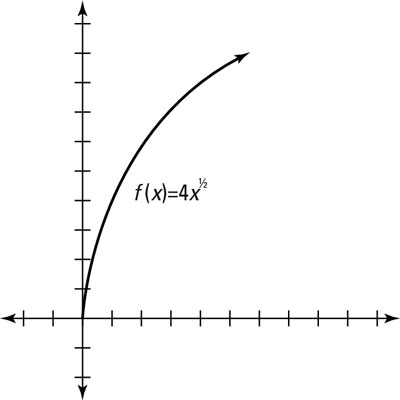
The 4 is a vertical stretch; it makes the graph four times as tall at every point. For example, 1 gets mapped to 4×sqrt(1)=4, 4 gets mapped to 4×sqrt(4)=8, 9 gets mapped to 4×sqrt(9)=12, etc. (notice that this example uses numbers that you can easily take the square root of to make graphing a simple task); and so on.

About This Article

This article is from the book: 

No items found.

About the book author:

This article can be found in the category: 

Pre-CalculusNo items found.Get a Subscription