30 Bài Tập Phương Trình đường Tròn Mức độ Thông Hiểu
Có thể bạn quan tâm

- Lớp 12
-
 Ngữ văn 12
Ngữ văn 12 - Soạn văn - Kết nối tri thức
- Soạn văn - Cánh diều
- Soạn văn - Chân trời sáng tạo
- Tác giả tác phẩm
- Tóm tắt, bố cục Văn - Kết nối tri thức
- Tóm tắt, bố cục Văn - Cánh diều
- Tóm tắt, bố cục Văn - Chân trời sáng tạo
- SBT Văn - Kết nối tri thức
- >> Xem thêm
-
 Toán học 12
Toán học 12 - SGK Toán - Kết nối tri thức
- SGK Toán - Cánh diều
- SGK Toán - Chân trời sáng tạo
- SGK Toán - Cùng khám phá
- SBT Toán - Kết nối tri thức
- SBT Toán - Cánh diều
- SBT Toán - Chân trời sáng tạo
- Chuyên đề học tập Toán - Kết nối tri thức
- >> Xem thêm
-
 Tiếng Anh 12
Tiếng Anh 12 - Tiếng Anh - Global Success
- Tiếng Anh - Friends Global
- Tiếng Anh - iLearn Smart World
- Tiếng Anh - Bright
- Tiếng Anh - English Discovery
- SBT Global Success
- SBT Friends Global
- SBT iLearn Smart World
- >> Xem thêm
-
 Vật lí 12
Vật lí 12 - SGK Vật Lí - Kết nối tri thức
- SGK Vật Lí - Cánh diều
- SGK Vật Lí - Chân trời sáng tạo
- SBT Vật lí - Kết nối tri thức
- SBT Vật lí - Cánh diều
- SBT Vật lí - Chân trời sáng tạo
- Chuyên đề học tập Lí - Kết nối tri thức
- Chuyên đề học tập Lí - Cánh diều
- >> Xem thêm
-
 Hóa học 12
Hóa học 12 - SGK Hóa - Kết nối tri thức
- SGK Hóa - Cánh diều
- SGK Hóa - Chân trời sáng tạo
- SBT Hóa - Kết nối tri thức
- SBT Hóa - Cánh diều
- SBT Hóa - Chân trời sáng tạo
- Chuyên đề học tập Hóa - Kết nối tri thức
- Chuyên đề học tập Hóa - Cánh diều
- >> Xem thêm
-
 Sinh học 12
Sinh học 12 - SGK Sinh - Kết nối tri thức
- SGK Sinh - Cánh diều
- SGK Sinh - Chân trời sáng tạo
- Trắc nghiệm Sinh - Kết nối tri thức
- Trắc nghiệm Sinh - Cánh diều
- Trắc nghiệm Sinh - Chân trời sáng tạo
- Chuyên đề học tập Sinh - Kết nối tri thức
- Chuyên đề học tập Sinh - Cánh diều
- >> Xem thêm
-
 Lịch sử 12
Lịch sử 12 - SGK Lịch sử - Kết nối tri thức
- SGK Lịch sử - Chân trời sáng tạo
- SGK Lịch sử - Cánh diều
- SBT Lịch sử - Cánh diều
- Đề thi, đề kiểm tra Lịch sử - Kết nối tri thức
- Đề thi, đề kiểm tra Lịch sử - Chân trời sáng tạo
- Đề thi, đề kiểm tra Lịch sử - Cánh diều
- Chuyên đề học tập Lịch sử - Kết nối tri thức
- >> Xem thêm
-
 Địa lí 12
Địa lí 12 - SGK Địa lí - Kết nối tri thức
- SGK Địa lí - Chân trời sáng tạo
- SGK Địa lí - Cánh diều
- SBT Địa lí - Cánh diều
- Đề thi, đề kiểm tra Địa lí - Kết nối tri thức
- Đề thi, đề kiểm tra Địa lí - Chân trời sáng tạo
- Đề thi, đề kiểm tra Địa lí - Cánh diều
- SBT Địa lí - Chân trời sáng tạo
- >> Xem thêm
- GD kinh tế và pháp luật 12
- SGK Giáo dục kinh tế và pháp luật - Kết nối tri thức
- SGK Giáo dục kinh tế và pháp luật - Chân trời sáng tạo
- SGK Giáo dục kinh tế và pháp luật - Cánh diều
- SBT Giáo dục kinh tế và pháp luật - Cánh diều
- SBT Giáo dục kinh tế và pháp luật - Chân trời sáng tạo
- Chuyên đề học tập Giáo dục kinh tế pháp luật - Kết nối tri thức
- Chuyên đề học tập Giáo dục kinh tế pháp luật - Cánh diều
- Chuyên đề học tập Giáo dục kinh tế pháp luật - Chân trời sáng tạo
-
 Công nghệ 12
Công nghệ 12 - SGK Công nghệ - Kết nối tri thức
- SGK Công nghệ - Cánh diều
- Chuyên đề học tập Công nghệ - Kết nối tri thức
- Chuyên đề học tập Công nghệ - Cánh diều
-
 Tin học 12
Tin học 12 - SGK Tin học - Cánh diều
- SGK Tin học - Chân trời sáng tạo
- SGK Tin học - Kết nối tri thức
- SBT Tin học - Kết nối tri thức
- SBT Tin học - Cánh diều
- SBT Tin học - Chân trời sáng tạo
- Chuyên đề học tập Tin - Kết nối tri thức
- Chuyên đề học tập Tin - Chân trời sáng tạo
- >> Xem thêm
-
 HĐ trải nghiệm, hướng nghiệp 12
HĐ trải nghiệm, hướng nghiệp 12 - SGK Hoạt động trải nghiệm, hướng nghiệp - Kết nối tri thức
- SGK Hoạt động trải nghiệm, hướng nghiệp - Cánh diều
- SGK Hoạt động trải nghiệm, hướng nghiệp - Chân trời sáng tạo Bản 1
- SGK Hoạt động trải nghiệm, hướng nghiệp - Chân trời sáng tạo Bản 2
- GD Quốc phòng và An ninh 12
- SGK Giáo dục quốc phòng và an ninh - Kết nối tri thức
- SGK Giáo dục quốc phòng và an ninh - Cánh diều
- Giáo dục thể chất 12
- SGK Giáo dục thể chất - Kết nối tri thức
- SGK Giáo dục thể chất - Cánh diều
- Giáo dục địa phương 12
- Tài liệu Giáo dục địa phương
- Đề thi, đề kiểm tra 12
- Tổng hợp đề thi, đề kiểm tra
-
- Lớp 11
-
 Ngữ văn 11
Ngữ văn 11 - Soạn văn - Kết nối tri thức - chi tiết
- Soạn văn - Kết nối tri thức - siêu ngắn
- Soạn văn - Cánh Diều - chi tiết
- Soạn văn - Cánh Diều - siêu ngắn
- Soạn văn - Chân trời sáng tạo - chi tiết
- Soạn văn - Chân trời sáng tạo - siêu ngắn
- Tác giả tác phẩm
- Tóm tắt, bố cục Văn - Kết nối tri thức
- >> Xem thêm
-
 Toán học 11
Toán học 11 - SGK Toán - Kết nối tri thức
- SGK Toán - Cánh diều
- SGK Toán - Chân trời sáng tạo
- SGK Toán - Cùng khám phá
- Chuyên đề học tập Toán - Kết nối tri thức
- Chuyên đề học tập Toán - Cánh diều
- Chuyên đề học tập Toán - Chân trời sáng tạo
- SBT Toán - Kết nối tri thức
- >> Xem thêm
-
 Tiếng Anh 11
Tiếng Anh 11 - Tiếng Anh - Global Success
- Tiếng Anh - Friends Global
- Tiếng Anh - iLearn Smart Wolrd
- Tiếng Anh - Bright
- Tiếng Anh - English Discovery
- SBT Global Success
- SBT Friends Global
- SBT iLearn Smart World
- >> Xem thêm
-
 Vật lí 11
Vật lí 11 - SGK Vật Lí - Kết nối tri thức
- SGK Vật Lí - Cánh diều
- SGK Vật Lí - Chân trời sáng tạo
- Chuyên đề học tập Lí - Kết nối tri thức
- Chuyên đề học tập Lí - Cánh diều
- Chuyên đề học tập Lí - Chân trời sáng tạo
- SBT Vật lí - Kết nối tri thức
- SBT Vật lí - Cánh diều
- >> Xem thêm
-
 Hóa học 11
Hóa học 11 - SGK Hóa học - Kết nối tri thức
- SGK Hóa học - Cánh diều
- SGK Hóa học - Chân trời sáng tạo
- Chuyên đề học tập Hóa - Kết nối tri thức
- Chuyên đề học tập Hóa - Cánh diều
- Chuyên đề học tập Hóa - Chân trời sáng tạo
- SBT Hóa - Kết nối tri thức
- SBT Hóa - Cánh diều
- >> Xem thêm
-
 Sinh học 11
Sinh học 11 - SGK Sinh - Kết nối tri thức
- SGK Sinh - Cánh diều
- SGK Sinh - Chân trời sáng tạo
- Chuyên đề học tập Sinh - Kết nối tri thức
- Chuyên đề học tập Sinh - Cánh diều
- Chuyên đề học tập Sinh - Chân trời sáng tạo
- SBT Sinh - Kết nối tri thức
- SBT Sinh - Cánh diều
- >> Xem thêm
-
 HĐ trải nghiệm, hướng nghiệp 11
HĐ trải nghiệm, hướng nghiệp 11 - SBT Hoạt động trải nghiệm - Kết nối tri thức
- SGK Hoạt động trải nghiệm, hướng nghiệp - Kết nối tri thức
- SGK Hoạt động trải nghiệm, hướng nghiệp - Cánh diều
- SGK Hoạt động trải nghiệm, hướng nghiệp - Chân trời sáng tạo Bản 1
- SGK Hoạt động trải nghiệm, hướng nghiệp - Chân trời sáng tạo Bản 2
- SBT Hoạt động trải nghiệm - Cánh diều
- SBT Hoạt động trải nghiệm - Chân trời sáng tạo (Bản 1)
- SBT Hoạt động trải nghiệm - Chân trời sáng tạo (Bản 2)
-
 Lịch sử 11
Lịch sử 11 - SGK Lịch sử - Kết nối tri thức
- SGK Lịch sử - Chân trời sáng tạo
- SGK Lịch sử - Cánh diều
- SBT Lịch sử - Kết nối tri thức
- SBT Lịch sử - Chân trời sáng tạo
- SBT Lịch sử - Cánh diều
- Đề thi, đề kiểm tra Lịch sử - Kết nối tri thức
- Đề thi, đề kiểm tra Lịch sử - Chân trời sáng tạo
- >> Xem thêm
-
 Địa lí 11
Địa lí 11 - SGK Địa lí - Kết nối tri thức
- SGK Địa lí - Chân trời sáng tạo
- SGK Địa lí - Cánh diều
- SBT Địa lí - Kết nối tri thức
- SBT Địa lí - Chân trời sáng tạo
- SBT Địa lí - Cánh diều
- Đề thi, đề kiểm tra Địa lí - Kết nối tri thức
- Đề thi, đề kiểm tra Địa lí - Chân trời sáng tạo
- >> Xem thêm
- GD kinh tế và pháp luật 11
- SGK Giáo dục kinh tế và pháp luật - Kết nối tri thức
- SGK Giáo dục kinh tế và pháp luật - Chân trời sáng tạo
- SGK Giáo dục kinh tế và pháp luật - Cánh diều
- SBT Giáo dục kinh tế và pháp luật - Kết nối tri thức
- SBT Giáo dục kinh tế và pháp luật - Chân trời sáng tạo
- SBT Giáo dục kinh tế và pháp luật - Cánh diều
- Chuyên đề học tập Giáo dục kinh tế pháp luật - Kết nối tri thức
- Chuyên đề học tập Giáo dục kinh tế pháp luật - Chân trời sáng tạo
- >> Xem thêm
-
 Công nghệ 11
Công nghệ 11 - SGK Công nghệ - Kết nối tri thức
- SGK Công nghệ - Cánh diều
-
 Tin học 11
Tin học 11 - SGK Tin học - Kết nối tri thức
- SGK Tin học - Cánh diều
- SBT Tin học - Kết nối tri thức
- SBT Tin học - Cánh diều
- Chuyên đề học tập Tin - Kết nối tri thức
- Chuyên đề học tập Tin - Cánh diều
- Giáo dục thể chất 11
- SGK Giáo dục thể chất - Kết nối tri thức
- SGK Giáo dục thể chất - Cánh diều
- GD Quốc phòng và An ninh 11
- SGK Giáo dục quốc phòng và an ninh - Kết nối tri thức
- SGK Giáo dục quốc phòng và an ninh - Cánh diều
- Giáo dục địa phương 11
- Tài liệu Giáo dục địa phương
- Đề thi, đề kiểm tra 11
- Tổng hợp đề thi, đề kiểm tra
-
- Lớp 10
-
 Ngữ văn 10
Ngữ văn 10 - Soạn văn - Kết nối tri thức - siêu ngắn
- Soạn văn - Kết nối tri thức - chi tiết
- Soạn văn - Chân trời sáng tạo - siêu ngắn
- Soạn văn - Chân trời sáng tạo - chi tiết
- Soạn văn - Cánh Diều - siêu ngắn
- Soạn văn - Cánh Diều - chi tiết
- Tác giả tác phẩm
- Tóm tắt, bố cục Văn - Kết nối tri thức
- >> Xem thêm
-
 Toán học 10
Toán học 10 - SGK Toán - Kết nối tri thức
- SGK Toán - Chân trời sáng tạo
- SGK Toán - Cánh diều
- SBT Toán - Kết nối tri thức
- SBT Toán - Chân trời sáng tạo
- SBT Toán - Cánh diều
- Chuyên đề học tập Toán - Kết nối tri thức
- Chuyên đề học tập Toán - Chân trời sáng tạo
- >> Xem thêm
-
 Tiếng Anh 10
Tiếng Anh 10 - Tiếng Anh - Global Success
- Tiếng Anh - Friends Global
- Tiếng Anh - iLearn Smart World
- Tiếng Anh - English Discovery
- Tiếng Anh - Bright
- Tiếng Anh - Explore New Worlds
- SBT Global Success
- SBT Friends Global
- >> Xem thêm
-
 Vật lí 10
Vật lí 10 - SGK Vật Lí - Kết nối tri thức
- SGK Vật Lí - Chân trời sáng tạo
- SGK Vật Lí - Cánh diều
- SBT Vật lí - Kết nối tri thức
- SBT Vật lí - Chân trời sáng tạo
- SBT Vật lí - Cánh diều
- Trắc nghiệm Lí - Kết nối tri thức
- Bài tập trắc nghiệm Lí - Kết nối tri thức
- >> Xem thêm
-
 Hóa học 10
Hóa học 10 - SGK Hóa - Kết nối tri thức
- SGK Hóa - Chân trời sáng tạo
- SGK Hóa - Cánh diều
- SBT Hóa - Kết nối tri thức
- SBT Hóa - Chân trời sáng tạo
- SBT Hóa 10 - Cánh diều
- Chuyên đề học tập Hóa - Kết nối tri thức
- Chuyên đề học tập Hóa 10 – Chân trời sáng tạo
- >> Xem thêm
-
 Sinh học 10
Sinh học 10 - SGK Sinh - Kết nối tri thức
- SGK Sinh - Chân trời sáng tạo
- SGK Sinh - Cánh diều
- SBT Sinh - Kết nối tri thức
- SBT Sinh - Chân trời sáng tạo
- SBT Sinh - Cánh diều
- Chuyên đề học tập Sinh - Kết nối tri thức
- Chuyên đề học tập Sinh - Chân trời sáng tạo
- >> Xem thêm
-
 Lịch sử 10
Lịch sử 10 - SGK Lịch sử - Kết nối tri thức
- SGK Lịch sử - Chân trời sáng tạo
- SGK Lịch sử - Cánh Diều
- SBT Lịch sử - Kết nối tri thức
- SBT Lịch sử - Chân trời sáng tạo
- SBT Lịch sử - Cánh Diều
- Chuyên đề học tập Lịch sử - Kết nối tri thức
- Trắc nghiệm Sử - kết nối tri thức
- >> Xem thêm
-
 Địa lí 10
Địa lí 10 - SGK Địa lí - Kết nối tri thức
- SGK Địa lí - Cánh Diều
- SGK Địa lí - Chân trời sáng tạo
- SBT Địa lí - Kết nối tri thức
- SBT Địa lí - Chân trời sáng tạo
- Trắc nghiệm Địa lí - Kết nối tri thức
- Trắc nghiệm Địa lí - Chân trời sáng tạo
- Trắc nghiệm Địa lí - Cánh Diều
- >> Xem thêm
-
 Tin học 10
Tin học 10 - SGK Tin học - Kết nối tri thức
- SGK Tin học - Cánh Diều
- SBT Tin học - Kết nối tri thức
- SBT Tin học 10 - Cánh diều
-
 Công nghệ 10
Công nghệ 10 - SGK Công nghệ - Kết nối tri thức
- SGK Công nghệ - Cánh diều
- Chuyên đề học tập Công nghệ - Kết nối tri thức
- Chuyên đề học tập Công nghệ - Cánh diều
- GD kinh tế và pháp luật 10
- SGK Giáo dục kinh tế và pháp luật - KNTT
- SGK Giáo dục kinh tế và pháp luật - CTST
- SGK Giáo dục kinh tế và pháp luật - Cánh diều
- SBT Giáo dục kinh tế và pháp luật - Kết nối tri thức
- SBT Giáo dục kinh tế và pháp luật - Chân trời sáng tạo
- SBT Giáo dục kinh tế và pháp luật - Cánh diều
- Chuyên đề học tập Giáo dục kinh tế pháp luật - Kết nối tri thức
- Chuyên đề học tập Giáo dục kinh tế pháp luật - Chân trời sáng tạo
- >> Xem thêm
-
 HĐ trải nghiệm, hướng nghiệp 10
HĐ trải nghiệm, hướng nghiệp 10 - SGK Hoạt động trải nghiệm, hướng nghiệp - Kết nối tri thức
- SGK Hoạt động trải nghiệm, hướng nghiệp - Chân trời sáng tạo
- SGK Hoạt động trải nghiệm, hướng nghiệp - Cánh Diều
- SBT Hoạt động trải nghiệm - Kết nối tri thức
- SBT Hoạt động trải nghiệm - Cánh diều
- SBT Hoạt động trải nghiệm - Chân trời sáng tạo (Bản 1)
- SBT Hoạt động trải nghiệm - Chân trời sáng tạo (Bản 2)
- Giáo dục thể chất 10
- SGK Giáo dục thể chất - Kết nối tri thức
- SGK Giáo dục thể chất - Cánh diều
- GD Quốc phòng và An ninh 10
- SGK Giáo dục quốc phòng và an ninh - Kết nối tri thức
- SGK Giáo dục quốc phòng và an ninh - Cánh diều
- Giáo dục địa phương 10
- Tài liệu Giáo dục địa phương
- Đề thi, đề kiểm tra 10
- Tổng hợp đề thi, đề kiểm tra
-
- Lớp 9
-
 Toán học 9
Toán học 9 - SGK Toán - Kết nối tri thức
- SGK Toán - Chân trời sáng tạo
- SGK Toán - Cánh diều
- SGK Toán - Cùng khám phá
- SBT Toán - Kết nối tri thức
- SBT Toán - Chân trời sáng tạo
- SBT Toán - Cánh diều
- Vở thực hành Toán
- >> Xem thêm
-
 Ngữ văn 9
Ngữ văn 9 - Soạn văn - Kết nối tri thức
- Soạn văn - Chân trời sáng tạo
- Soạn văn - Cánh diều
- Tác giả - Tác phẩm văn
- Tóm tắt, bố cục Văn - Kết nối tri thức
- Tóm tắt, bố cục Văn - Chân trời sáng tạo
- Tóm tắt, bố cục Văn - Cánh diều
- SBT Văn - Kết nối tri thức
- >> Xem thêm
-
 Tiếng Anh 9
Tiếng Anh 9 - Tiếng Anh - Global Success
- Tiếng Anh - Friends Plus
- Tiếng Anh - iLearn Smart World
- Tiếng Anh - Right on!
- Tiếng Anh - English Discovery
- SBT Global Success
- SBT Friends Plus
- SBT iLearn Smart World
- >> Xem thêm
-
 Khoa học tự nhiên 9
Khoa học tự nhiên 9 - SGK Khoa học tự nhiên - Kết nối tri thức
- SGK Khoa học tự nhiên - Cánh diều
- SGK Khoa học tự nhiên 9 Chân trời sáng tạo
- SBT KHTN - Kết nối tri thức
- SBT KHTN - Cánh diều
- SBT KHTN - Chân trời sáng tạo
- Trắc nghiệm KHTN - Kết nối tri thức
- Trắc nghiệm KHTN - Cánh diều
- >> Xem thêm
-
 Lịch sử và Địa lí 9
Lịch sử và Địa lí 9 - SGK Lịch sử và Địa lí - Kết nối tri thức
- SGK Lịch sử và Địa lí - Cánh diều
- SGK Lịch sử và Địa lí - Chân trời sáng tạo
- SBT Lịch sử - Cánh diều
- SBT Địa lí - Kết nối tri thức
- SBT Địa lí - Chân trời sáng tạo
- SBT Đia lí - Cánh diều
- Đề thi, kiểm tra Lịch Sử và Địa lí - Kết nối tri thức
- >> Xem thêm
-
 GDCD 9
GDCD 9 - Giáo dục công dân - Kết nối tri thức
- Giáo dục công dân - Chân trời sáng tạo
- Giáo dục công dân - Cánh diều
- SBT GDCD - Chân trời sáng tạo
- SBT GDCD - Cánh diều
-
 Tin học 9
Tin học 9 - SGK Tin học - Kết nối tri thức
- SGK Tin học - Cánh diều
- SGK Tin học - Chân trời sáng tạo
- SBT Tin học - Kết nối tri thức
- SBT Tin học - Chân trời sáng tạo
- SBT Tin học - Cánh diều
-
 Công nghệ 9
Công nghệ 9 - SGK Công nghệ - Kết nối tri thức
- SGK Công nghệ - Chân trời sáng tạo
- SGK Công nghệ - Cánh diều
- SBT Công nghệ - Cánh diều
-
 HĐ trải nghiệm, hướng nghiệp 9
HĐ trải nghiệm, hướng nghiệp 9 - SGK Hoạt động trải nghiệm, hướng nghiệp - Kết nối tri thức
- SGK Hoạt động trải nghiệm, hướng nghiệp - Cánh diều
- SGK Hoạt động trải nghiệm, hướng nghiệp - Chân trời sáng tạo Bản 1
- SGK Hoạt động trải nghiệm, hướng nghiệp - Chân trời sáng tạo Bản 2
- Giáo dục địa phương 9
- Tài liệu Giáo dục địa phương
- Đề thi, đề kiểm tra 9
- Tổng hợp đề thi, đề kiểm tra
- Tổng hợp đề thi vào 10
-
- Lớp 8
-
 Ngữ văn 8
Ngữ văn 8 - Soạn văn chi tiết - KNTT
- Soạn văn siêu ngắn - KNTT
- Soạn văn chi tiết - CTST
- Soạn văn siêu ngắn - CTST
- Soạn văn chi tiết - Cánh diều
- Soạn văn siêu ngắn - Cánh diều
- Tác giả - Tác phẩm văn
- Tóm tắt, bố cục Văn - Kết nối tri thức
- >> Xem thêm
-
 Toán học 8
Toán học 8 - SGK Toán - Kết nối tri thức
- SGK Toán - Chân trời sáng tạo
- SGK Toán - Cánh diều
- SGK Toán - Cùng khám phá
- SBT Toán - Kết nối tri thức
- SBT Toán - Chân trời sáng tạo
- SBT Toán - Cánh diều
- Vở thực hành Toán
- >> Xem thêm
-
 Tiếng Anh 8
Tiếng Anh 8 - Tiếng Anh - Global Success
- Tiếng Anh - Friends Plus
- Tiếng Anh - iLearn Smart World
- Tiếng Anh - Right on!
- Tiếng Anh - English Discovery
- SBT Global Success
- SBT Friends Plus
- SBT iLearn Smart World
- >> Xem thêm
-
 Khoa học tự nhiên 8
Khoa học tự nhiên 8 - SGK Khoa học tự nhiên - Kết nối tri thức
- SGK Khoa học tự nhiên - Chân trời sáng tạo
- SGK Khoa học tự nhiên - Cánh diều
- SBT KHTN - Kết nối tri thức
- SBT KHTN - Cánh diều
- Vở thực hành Khoa học tự nhiên
- Đề thi, đề kiểm tra KHTN - Kết nối tri thức
- Đề thi, đề kiểm tra KHTN - Cánh diều
- >> Xem thêm
-
 Lịch sử và Địa lí 8
Lịch sử và Địa lí 8 - SGK Lịch sử và Địa lí - Kết nối tri thức
- SGK Lịch sử và Địa lí - Cánh diều
- SGK Lịch sử và Địa lí - Chân trời sáng tạo
- SBT Lịch sử - Kết nối tri thức
- SBT Địa lí - Kết nối tri thức
- SBT Lịch sử - Chân trời sáng tạo
- SBT Địa lí - Chân trời sáng tạo
- SBT Lịch sử - Cánh diều
- >> Xem thêm
-
 GDCD 8
GDCD 8 - Giáo dục công dân - Kết nối tri thức
- Giáo dục công dân - Chân trời sáng tạo
- Giáo dục công dân - Cánh diều
- SBT GDCD - Kết nối tri thức
- SBT GDCD - Chân trời sáng tạo
- SBT GDCD - Cánh diều
-
 Công nghệ 8
Công nghệ 8 - SGK Công nghệ - Kết nối tri thức
- SGK Công nghệ - Chân trời sáng tạo
- SGK Công nghệ - Cánh diều
- SBT Công nghệ - Kết nối tri thức
- SBT Công nghệ - Chân trời sáng tạo
- SBT Công nghệ - Cánh diều
-
 Tin học 8
Tin học 8 - SGK Tin học - Kết nối tri thức
- SGK Tin học - Chân trời sáng tạo
- SGK Tin học - Cánh diều
- SBT Tin học - Kết nối tri thức
- SBT Tin học - Chân trời sáng tạo
- SBT Tin học - Cánh diều
-
 HĐ trải nghiệm, hướng nghiệp 8
HĐ trải nghiệm, hướng nghiệp 8 - SGK Hoạt động trải nghiệm, hướng nghiệp - Kết nối tri thức
- SGK Hoạt động trải nghiệm, hướng nghiệp - Cánh diều
- SGK Hoạt động trải nghiệm, hướng nghiệp - Chân trời sáng tạo Bản 1
- SGK Hoạt động trải nghiệm, hướng nghiệp - Chân trời sáng tạo Bản 2
- SBT Hoạt động trải nghiệm - Kết nối tri thức
- SBT Hoạt động trải nghiệm - Cánh diều
- SBT Hoạt động trải nghiệm - Chân trời sáng tạo (Bản 1)
- SBT Hoạt động trải nghiệm - Chân trời sáng tạo (Bản 2)
-
 Âm nhạc 8
Âm nhạc 8 - SGK Âm nhạc - Kết nối tri thức
- SGK Âm nhạc - Chân trời sáng tạo
- SGK Âm nhạc - Cánh diều
-
 Mỹ thuật 8
Mỹ thuật 8 - SGK Mĩ thuật - Kết nối tri thức
- SGK Mĩ thuật - Chân trời sáng tạo bản 1
- SGK Mĩ thuật - Cánh diều
- SGK Mĩ thuật - Chân trời sáng tạo bản 2
- Giáo dục thể chất 8
- SGK Giáo dục thể chất - Kết nối tri thức
- SGK Giáo dục thể chất - Cánh diều
- SGK Giáo dục thể chất - Chân trời sáng tạo
- Giáo dục địa phương 8
- Đề thi, đề kiểm tra Giáo dục địa phương
- Tài liệu Giáo dục địa phương
- Đề thi, đề kiểm tra 8
- Tổng hợp đề thi, đề kiểm tra
-
- Lớp 7
-
 Ngữ văn 7
Ngữ văn 7 - Soạn văn siêu ngắn - KNTT
- Soạn văn chi tiết - KNTT
- Soạn văn siêu ngắn - CTST
- Soạn văn chi tiết - CTST
- Soạn văn siêu ngắn - Cánh diều
- Soạn văn chi tiết - Cánh diều
- Tác giả - Tác phẩm văn
- Tóm tắt, bố cục Văn - Kết nối tri thức
- >> Xem thêm
-
 Toán học 7
Toán học 7 - SGK Toán - Kết nối tri thức
- SGK Toán - Chân trời sáng tạo
- SGK Toán - Cánh diều
- SBT Toán - Kết nối tri thức
- SBT Toán - Chân trời sáng tạo
- SBT Toán - Cánh diều
- Trắc nghiệm Toán - Kết nối tri thức
- Trắc nghiệm Toán- Chân trời sáng tạo
- >> Xem thêm
-
 Tiếng Anh 7
Tiếng Anh 7 - Tiếng Anh - Global Success
- Tiếng Anh - Friends Plus
- Tiếng Anh - iLearn Smart World
- Tiếng Anh - English Discovery
- Tiếng Anh - Right on!
- SBT Global Success
- SBT Friends Plus
- SBT iLearn Smart World
- >> Xem thêm
-
 Khoa học tự nhiên 7
Khoa học tự nhiên 7 - SGK Khoa học tự nhiên - Kết nối tri thức
- SGK Khoa học tự nhiên - Chân trời sáng tạo
- SGK Khoa học tự nhiên - Cánh diều
- SBT KHTN - Kết nối tri thức
- SBT KHTN - Chân trời sáng tạo
- SBT KHTN - Cánh diều
- Trắc nghiệm KHTN - Kết nối tri thức
- Bài tập trắc nghiệm Khoa học tự nhiên - Kết nối tri thức
- >> Xem thêm
-
 Lịch sử và Địa lí 7
Lịch sử và Địa lí 7 - SGK Lịch sử và Địa lí - Kết nối tri thức
- SGK Lịch sử và Địa lí - Chân trời sáng tạo
- SGK Lịch sử và Địa lí - Cánh Diều
- SBT Lịch sử và Địa lí - Kết nối tri thức
- SBT Lịch sử và Địa lí - Chân trời sáng tạo
- SBT Lịch sử và Địa lí - Cánh diều
- Trắc nghiệm Lịch sử và Địa lí - Kết nối tri thức
- Trắc nghiệm Lịch sử và Địa lí - Chân trời sáng tạo
- >> Xem thêm
-
 Tin học 7
Tin học 7 - SGK Tin học - Kết nối tri thức
- SGK Tin học - Cánh Diều
- SGK Tin học - Chân trời sáng tạo
- SBT Tin học - Kết nối tri thức
- SBT Tin học - Chân trời sáng tạo
- SBT Tin học - Cánh diều
-
 Công nghệ 7
Công nghệ 7 - SGK Công nghệ - Kết nối tri thức
- SGK Công nghệ - Chân trời sáng tạo
- SGK Công nghệ - Cánh diều
- SBT Công nghệ - Kết nối tri thức
- SBT Công nghệ - Chân trời sáng tạo
- SBT Công nghệ - Cánh diều
-
 GDCD 7
GDCD 7 - SGK GDCD - KNTT
- SGK GDCD - CTST
- SGK GDCD - Cánh diều
- Bài tập tình huống GDCD
- SBT GDCD - Kết nối tri thức
- SBT GDCD - Chân trời sáng tạo
- SBT GDCD - Cánh diều
-
 HĐ trải nghiệm, hướng nghiệp 7
HĐ trải nghiệm, hướng nghiệp 7 - SBT Hoạt động trải nghiệm - Chân trời sáng tạo (Bản 1)
- SGK Hoạt động trải nghiệm, hướng nghiệp - Kết nối tri thức
- SGK Hoạt động trải nghiệm, hướng nghiệp - Cánh Diều
- SGK Hoạt động trải nghiệm, hướng nghiệp - Chân trời sáng tạo
- SBT Hoạt động trải nghiệm - Cánh diều
- SBT Hoạt động trải nghiệm - Kết nối tri thức
- SBT Hoạt động trải nghiệm - Chân trời sáng tạo (Bản 2)
-
 Âm nhạc 7
Âm nhạc 7 - Âm nhạc - Kết nối tri thức
- Âm nhạc - Chân trời sáng tạo
- Âm nhạc - Cánh diều
- Giáo dục địa phương 7
- Đề thi, đề kiểm tra Giáo dục địa phương 7
- Tài liệu Giáo dục địa phương
- Đề thi, đề kiểm tra 7
- Tổng hợp đề thi, đề kiểm tra
-
- Lớp 6
-
 Ngữ văn 6
Ngữ văn 6 - Soạn văn siêu ngắn - KNTT
- Soạn văn chi tiết - KNTT
- Soạn văn siêu ngắn - CTST
- Soạn văn chi tiết - CTST
- Soạn văn siêu ngắn - Cánh diều
- Soạn văn chi tiết - Cánh diều
- Tác giả - Tác phẩm văn
- Tóm tắt, bố cục Văn - Kết nối tri thức
- >> Xem thêm
-
 Toán học 6
Toán học 6 - SGK Toán - Kết nối tri thức
- SGK Toán - Chân trời sáng tạo
- SGK Toán - Cánh diều
- SBT Toán - Kết nối tri thức
- SBT Toán - Chân trời sáng tạo
- SBT Toán - Cánh diều
- Trắc nghiệm Toán - Kết nối tri thức
- Trắc nghiệm Toán - Chân trời sáng tạo
- >> Xem thêm
-
 Tiếng Anh 6
Tiếng Anh 6 - Global Success (Pearson)
- Tiếng Anh - Friends plus
- Tiếng Anh - iLearn Smart World
- Tiếng Anh - Right on
- Tiếng Anh - English Discovery
- Tiếng Anh - Explore English
- SBT Global Success
- SBT Friends Plus
- >> Xem thêm
-
 Khoa học tự nhiên 6
Khoa học tự nhiên 6 - SGK KHTN - Kết nối tri thức
- SGK KHTN - Chân trời sáng tạo
- SGK KHTN - Cánh Diều
- SBT KHTN - Kết nối tri thức
- SBT KHTN - Chân trời sáng tạo
- SBT KHTN - Cánh Diều
- Trắc nghiệm KHTN - Kết nối tri thức
- Trắc nghiệm KHTN - Chân trời sáng tạo
- >> Xem thêm
-
 Lịch sử và Địa lí 6
Lịch sử và Địa lí 6 - SGK Lịch sử và Địa lí - KNTT
- SGK Lịch sử và Địa lí - CTST
- SGK Lịch sử và Địa lí - Cánh Diều
- SBT Lịch sử và Địa lí - KNTT
- SBT Lịch sử và Địa lí - CTST
- SBT Lịch sử và Địa lí - Cánh diều
- Trắc nghiệm Lịch sử và Địa Lí - KNTT
- Trắc nghiệm Lịch Sử và Địa Lí - CTST
- >> Xem thêm
-
 GDCD 6
GDCD 6 - SGK GDCD - KNTT
- SGK GDCD - CTST
- SGK GDCD - Cánh Diều
- SBT GDCD - Kết nối tri thức
- SBT GDCD - Chân trời sáng tạo
- SBT GDCD - Cánh diều
-
 Công nghệ 6
Công nghệ 6 - Công nghệ - Kết nối tri thức
- Công nghệ - Cánh Diều
- Công nghệ - Chân trời sáng tạo
- SBT Công nghệ - Kết nối tri thức
- SBT Công nghệ - Cánh diều
- SBT Công nghệ - Chân trời sáng tạo
-
 Tin học 6
Tin học 6 - Tin học - Kết nối tri thức + chân trời sáng tạo
- Tin học - Cánh Diều
- SBT Tin học - Kết nối tri thức
- SBT Tin học - Cánh Diều
-
 HĐ trải nghiệm, hướng nghiệp 6
HĐ trải nghiệm, hướng nghiệp 6 - SGK Trải nghiệm, hướng nghiệp - Kết nối tri thức
- SGK Trải nghiệm, hướng nghiệp - Chân trời sáng tạo
- SGK Trải nghiệm, hướng nghiệp - Cánh diều
- SBT Trải nghiệm, hướng nghiệp - Kết nối tri thức
- SBT Trải nghiệm, hướng nghiệp - Chân trời sáng tạo
- Thực hành Trải nghiệm, hướng nghiệp - Cánh diều
-
 Âm nhạc 6
Âm nhạc 6 - Âm nhạc - Kết nối tri thức
- Âm nhạc - Cánh Diều
- Âm nhạc: Chân trời sáng tạo
-
 Mỹ thuật 6
Mỹ thuật 6 - Mĩ thuật - Kết nối tri thức
- Mĩ thuật - Chân trời sáng tạo
- Mĩ thuật - Cánh diều
- Giáo dục địa phương 6
- Đề thi, đề kiểm tra Giáo dục địa phương
- Tài liệu Giáo dục địa phương
- Đề thi, đề kiểm tra 6
- Tổng hợp đề thi, đề kiểm tra
-
- Lớp 5
-
 Toán học 5
Toán học 5 - SGK Toán - Kết nối tri thức
- SGK Toán - Chân trời sáng tạo
- SGK Toán - Cánh diều
- SGK Toán - Bình Minh
- VBT Toán - Kết nối tri thức
- VBT Toán - Cánh diều
- Trắc nghiệm Toán - Kết nối tri thức
- Trắc nghiệm Toán - Chân trời sáng tạo
- >> Xem thêm
-
 Tiếng việt 5
Tiếng việt 5 - Tiếng Việt - Kết nối tri thức
- Tiếng Việt - Chân trời sáng tạo
- Tiếng Việt - Cánh diều
- VBT Tiếng Việt - Kết nối tri thức
- VBT Tiếng Việt - Chân trời sáng tạo
- VBT Tiếng Việt - Cánh diều
- Văn mẫu lớp 5
- Đề thi, đề kiểm tra Tiếng Việt - Kết nối tri thức
- >> Xem thêm
-
 Tiếng Anh 5
Tiếng Anh 5 - Tiếng Anh - Global Success
- Tiếng Anh - Family and Friends
- Tiếng Anh - iLearn Smart Start
- Tiếng Anh - Explore Our World
- Tiếng Anh - Phonics Smart
- SBT Tiếng Anh - Global Success
- SBT Tiếng Anh - Family and Friends
- SBT Tiếng Anh - iLearn Smart Start
- >> Xem thêm
-
 Lịch sử và Địa lí 5
Lịch sử và Địa lí 5 - SGK Lịch sử và Địa lí - Kết nối tri thức
- SGK Lịch sử và Địa lí - Cánh diều
- SGK Lịch sử và Địa lí - Chân trời sáng tạo
- VBT Lịch sử và Địa lí - Kết nối tri thức
- VBT Lịch sử và Địa lí - Cánh diều
- Đề thi, đề kiểm tra Lịch sử và Địa lí - Kết nối tri thức
- Đề thi, đề kiểm tra Lịch sử và Địa lí - Chân trời sáng tạo
- Đề thi, đề kiểm tra Lịch sử và Địa lí - Cánh diều
-
 Khoa học 5
Khoa học 5 - SGK Khoa học - Kết nối tri thức
- SGK Khoa học - Chân trời sáng tạo
- SGK Khoa học - Cánh diều
- VBT Khoa học - Kết nối tri thức
- VBT Khoa học - Chân trời sáng tạo
- VBT Khoa học - Cánh diều
-
 Đạo đức 5
Đạo đức 5 - SGK Đạo đức - Kết nối tri thức
- SGK Đạo đức - Chân trời sáng tạo
- SGK Đạo đức - Cánh diều
- VBT Đạo đức - Kết nối tri thức
- VBT Đạo đức - Chân trời sáng tạo
- VBT Đạo đức - Cánh diều
-
 Tin học 5
Tin học 5 - SGK Tin học - Cánh diều
- SGK Tin học - Kết nối tri thức
- SGK Tin học - Chân trời sáng tạo
- VBT Tin học - Kết nối tri thức
- VBT Tin học - Chân trời sáng tạo
- VBT Tin học - Cánh diều
-
 HĐ trải nghiệm, hướng nghiệp 5
HĐ trải nghiệm, hướng nghiệp 5 - SGK Hoạt động trải nghiệm - Kết nối tri thức
- SGK Hoạt động trải nghiệm - Cánh diều
- SGK Hoạt động trải nghiệm - Chân trời sáng tạo Bản 1
- SGK Hoạt động trải nghiệm - Chân trời sáng tạo Bản 2
- VBT Hoạt động trải nghiệm - Kết nối tri thức
- VBT Hoạt động trải nghiệm - Cánh diều
- VBT Hoạt động trải nghiệm - Chân trời sáng tạo (Bản 1)
- VBT Hoạt động trải nghiệm - Chân trời sáng tạo (Bản 2)
-
 Công nghệ 5
Công nghệ 5 - SGK Công nghệ - Kết nối tri thức
- SGK Công nghệ - Chân trời sáng tạo
- SGK Công nghệ - Cánh diều
- VBT Công nghệ - Kết nối tri thức
- Đề thi, đề kiểm tra 5
- Đề thi vào lớp 6
- Tổng hợp đề thi, đề kiểm tra
-
- Lớp 4
-
 Toán học 4
Toán học 4 - SGK Toán - Kết nối tri thức
- SGK Toán - Chân trời sáng tạo
- SGK Toán - Cánh diều
- SGK Toán - Bình Minh
- VBT Toán - Kết nối tri thức
- Vở thực hành Toán
- Trắc nghiệm Toán - Kết nối tri thức
- Trắc nghiệm Toán - Cánh diều
- >> Xem thêm
-
 Tiếng việt 4
Tiếng việt 4 - Tiếng Việt - Kết nối tri thức
- Tiếng Việt - Chân trời sáng tạo
- Tiếng Việt - Cánh diều
- VBT Tiếng Việt - Kết nối tri thức
- Đề thi, đề kiểm tra Tiếng Việt - Kết nối tri thức
- Đề thi, đề kiểm tra Tiếng Việt - Chân trời sáng tạo
- Đề thi, đề kiểm tra Tiếng Việt - Cánh diều
- Ôn hè Tiếng Việt
- >> Xem thêm
-
 Tiếng Anh 4
Tiếng Anh 4 - Tiếng Anh - Global Sucess
- Tiếng Anh - Family and Friends
- Tiếng Anh - iLearn Smart Start
- Tiếng Anh - Phonics Smart
- Tiếng Anh - Explore Our World
- SBT Tiếng Anh - Global Success
- SBT Tiếng Anh - Family and Friends
- SBT Tiếng Anh - iLearn Smart Start
- >> Xem thêm
-
 Lịch sử và Địa lí 4
Lịch sử và Địa lí 4 - SGK Lịch sử và Địa lí - Kết nối tri thức
- SGK Lịch sử và Địa lí - Chân trời sáng tạo
- SGK Lịch sử và Địa lí - Cánh diều
- VBT Lịch sử và Địa lí - Kết nối tri thức
- VBT Lịch sử và Địa lí - Chân trời sáng tạo
- VBT Lịch sử và Địa lí - Cánh diều
- Đề thi, đề kiểm tra Lịch sử và Địa lí - Kết nối tri thức
- Đề thi, đề kiểm tra Lịch sử và Địa lí - Chân trời sáng tạo
- >> Xem thêm
-
 Khoa học 4
Khoa học 4 - SGK Khoa học - Kết nối tri thức
- SGK Khoa học - Chân trời sáng tạo
- SGK Khoa học - Cánh diều
- VBT Khoa học - Kết nối tri thức
- VBT Khoa học - Chân trời sáng tạo
- VBT Khoa học - Cánh diều
-
 Đạo đức 4
Đạo đức 4 - SGK Đạo đức - Kết nối tri thức
- SGK Đạo đức - Chân trời sáng tạo
- SGK Đạo đức - Cánh diều
- VBT Đạo đức - Kết nối tri thức
- VBT Đạo đức 4 - Chân trời sáng tạo
- VBT Đạo đức - Cánh diều
-
 Tin học 4
Tin học 4 - SGK Tin học - Kết nối tri thức
- SGK Tin học - Chân trời sáng tạo
- SGK Tin học - Cánh diều
- VBT Tin học - Kết nối tri thức
- VBT Tin học - Chân trời sáng tạo
- VBT Tin học - Cánh diều
-
 Công nghệ 4
Công nghệ 4 - SGK Công nghệ - Kết nối tri thức
- SGK Công nghệ - Chân trời sáng tạo
- SGK Công nghệ - Cánh diều
- VBT Công nghệ - Kết nối tri thức
- VBT Công nghệ - Chân trời sáng tạo
- VBT Công nghệ - Cánh diều
-
 HĐ trải nghiệm, hướng nghiệp 4
HĐ trải nghiệm, hướng nghiệp 4 - SGK Hoạt động trải nghiệm - Kết nối tri thức
- SGK Hoạt động trải nghiệm - Cánh diều
- SGK Hoạt động trải nghiệm - Chân trời sáng tạo Bản 1
- SGK Hoạt động trải nghiệm - Chân trời sáng tạo Bản 2
- VBT Hoạt động trải nghiệm - Kết nối tri thức
- VBT Hoạt động trải nghiệm - Cánh diều
- VBT Hoạt động trải nghiệm - Chân trời sáng tạo (Bản 1)
- VBT Hoạt động trải nghiệm - Chân trời sáng tạo (Bản 2)
-
 Âm nhạc 4
Âm nhạc 4 - SGK Âm nhạc - Kết nối tri thức
- SGK Âm nhạc - Chân trời sáng tạo
- SGK Âm nhạc - Cánh diều
-
 Mỹ thuật 4
Mỹ thuật 4 - SGK Mĩ thuật - Kết nối tri thức
- SGK Mĩ thuật - Cánh diều
- SGK Mĩ thuật - Chân trời sáng tạo bản 1
- SGK Mĩ thuật - Chân trời sáng tạo bản 2
- Giáo dục thể chất 4
- SGK Giáo dục thể chất - Kết nối tri thức
- SGK Giáo dục thể chất - Cánh diều
- SGK Giáo dục thể chất - Chân trời sáng tạo
- Giáo dục địa phương 4
- Tài liệu Giáo dục địa phương
- Đề thi, đề kiểm tra 4
- Tổng hợp đề thi, đề kiểm tra
-
- Lớp 3
-
 Toán học 3
Toán học 3 - SGK Toán - Kết nối tri thức
- SGK Toán - Chân trời sáng tạo
- SGK Toán - Cánh diều
- VBT Toán - Kết nối tri thức
- Trắc nghiệm Toán - Kết nối tri thức
- Trắc nghiệm Toán - Cánh diều
- Trắc nghiệm Toán - Chân trời sáng tạo
- Đề thi, đề kiểm tra Toán - Kết nối tri thức
- >> Xem thêm
-
 Tiếng việt 3
Tiếng việt 3 - Tiếng Việt - Kết nối tri thức
- Tiếng Việt - Chân trời sáng tạo
- Tiếng Việt - Cánh diều
- VBT Tiếng Việt - Kết nối tri thức
- VBT Tiếng Việt - Chân trời sáng tạo
- VBT Tiếng Việt - Cánh diều
- Đề thi, đề kiểm tra Tiếng Việt - Kết nối tri thức
- Đề thi, đề kiểm tra Tiếng Việt - Chân trời sáng tạo
- >> Xem thêm
-
 Tiếng Anh 3
Tiếng Anh 3 - Tiếng Anh - Global Success
- Tiếng Anh - Family and Friends
- Tiếng Anh - iLearn Smart Start
- Tiếng Anh - Explore Our World
- Tiếng Anh - Phonics Smart
- SBT Tiếng Anh - Global Success
- SBT Tiếng Anh - Family and Friends
- SBT Tiếng Anh - iLearn Smart Start
- >> Xem thêm
-
 Tự nhiên và xã hội 3
Tự nhiên và xã hội 3 - VBT Tự nhiên và xã hội - Cánh diều
- Tự nhiên và xã hội - Kết nối tri thức
- Tự nhiên và xã hội - Chân trời sáng tạo
- Tự nhiên và xã hội - Cánh diều
- VBT Tự nhiên và xã hội - Kết nối tri thức
- VBT Tự nhiên và xã hội - Chân trời sáng tạo
-
 Đạo đức 3
Đạo đức 3 - SGK Đạo đức - Kết nối tri thức
- SGK Đạo đức - Chân trời sáng tạo
- SGK Đạo đức - Cánh diều
- VBT Đạo đức - Kết nối tri thức
- VBT Đạo đức - Cánh diều
- VBT Đạo đức - Chân trời sáng tạo
-
 Tin học 3
Tin học 3 - SGK Tin học - Kết nối tri thức
- SGK Tin học - Chân trời sáng tạo
- SGK Tin học - Cánh diều
- VBT Tin học - Kết nối tri thức
- VBT Tin học - Chân trời sáng tạo
-
 HĐ trải nghiệm, hướng nghiệp 3
HĐ trải nghiệm, hướng nghiệp 3 - SGK Hoạt động trải nghiệm- Kết nối tri thức
- SGK Hoạt động trải nghiệm- Chân trời sáng tạo
- SGK Hoạt động trải nghiệm - Cánh diều
- VBT Hoạt động trải nghệm - Kết nối tri thức
- VBT Hoạt động trải nghiệm - Chân trời sáng tạo
- VBT Hoạt động trải nghiệm - Cánh diều
-
 Công nghệ 3
Công nghệ 3 - SGK Công nghệ - Kết nối tri thức
- SGK Công nghệ - Chân trời sáng tạo
- SGK Công nghệ - Cánh diều
- VBT Công nghệ - Kết nối tri thức
- VBT Công nghệ - Chân trời sáng tạo
- VBT Công nghệ - Cánh diều
-
 Âm nhạc 3
Âm nhạc 3 - Âm nhạc - Kết nối tri thức
- Âm nhạc - Chân trời sáng tạo
- Âm nhạc - Cánh diều
- Giáo dục thể chất 3
- SGK Giáo dục thể chất - Kết nối tri thức
- SGK Giáo dục thể chất - Chân trời sáng tạo
- SGK Giáo dục thể chất - Cánh diều
- Giáo dục địa phương 3
- Tài liệu Giáo dục địa phương
-
- Lớp 2
-
 Toán học 2
Toán học 2 - SGK Toán - Kết nối tri thức
- SGK Toán - Chân trời sáng tạo
- SGK Toán - Cánh Diều
- VBT Toán - KNTT
- VBT Toán - CTST
- Trắc nghiệm Toán - Kết nối tri thức
- Trắc nghiệm Toán - Chân trời sáng tạo
- Trắc nghiệm Toán - Cánh Diều
- >> Xem thêm
-
 Tiếng việt 2
Tiếng việt 2 - Tiếng Việt - Kết nối tri thức
- Tiếng Việt - Chân trời sáng tạo
- Tiếng Việt - Cánh Diều
- Văn mẫu - Kết nối tri thức
- Văn mẫu - Chân trời sáng tạo
- Văn mẫu - Cánh diều
- VBT Tiếng Việt - Kết nối tri thức
- VBT Tiếng Việt - Chân trời sáng tạo
- >> Xem thêm
-
 Tiếng Anh 2
Tiếng Anh 2 - Tiếng Anh - Kết nối tri thức
- Tiếng Anh - Family and Friends
- Tiếng Anh - iLearn Smart Start
- Tiếng Anh - Phonics Smart
- Tiếng Anh - English Discovery
- Tiếng Anh - Explore Our World
- Family & Friends Special
- SBT Kết nối tri thức
- >> Xem thêm
-
 Tự nhiên và xã hội 2
Tự nhiên và xã hội 2 - Tự nhiên và xã hội - Kết nối tri thức
- Tự nhiên và xã hội - Chân trời sáng tạo
- Tự nhiên và xã hội - Cánh diều
- VBT Tự nhiên và xã hội - Kết nối tri thức
- VBT Tự nhiên và xã hội - Cánh diều
- VBT Tự nhiên và xã hội - Chân trời sáng tạo
-
 Đạo đức 2
Đạo đức 2 - SGK Đạo đức - Kết nối tri thức
- SGK Đạo đức - Chân trời sáng tạo
- SGK Đạo đức - Cánh Diều
- VBT Đạo đức - Kết nối tri thức
- VBT Đạo đức - Chân trời sáng tạo
- VBT Đạo đức - Cánh Diều
-
 Âm nhạc 2
Âm nhạc 2 - Âm nhạc 2 - Kết nối tri thức
- Âm nhạc 2 - Chân trời sáng tạo
- Âm nhạc 2 - Cánh diều
- VBT Âm nhạc - Kết nối tri thức
- VBT Âm nhạc - Chân trời sáng tạo
- VBT Âm nhạc - Cánh diều
-
 Mỹ thuật 2
Mỹ thuật 2 - Mĩ thuật- Kết nối tri thức
- Mĩ thuật- Chân trời sáng tạo
- Mĩ thuật - Cánh Diều
-
 HĐ trải nghiệm, hướng nghiệp 2
HĐ trải nghiệm, hướng nghiệp 2 - VBT Hoạt động trải nghiệm - Chân trời sáng tạo
- VTH Hoạt động trải nghiệm - Cánh Diều
- VBT Hoạt động trải nghiệm - Kết nối tri thức
- Giáo dục địa phương 2
- Tài liệu Giáo dục địa phương
-
- Lớp 1
-
 Tiếng việt 1
Tiếng việt 1 - Đề thi, kiểm tra Tiếng Việt
- SGK Tiếng Việt - Kết nối tri thức
- SGK Tiếng Việt - Chân trời sáng tạo
- SGK Tiếng Việt - Cánh diều
-
 Toán học 1
Toán học 1 - SGK Toán - Kết nối tri thức
- SGK Toán - Cánh diều
- SGK Toán - Chân trời sáng tạo
- Trắc nghiệm Toán
-
 Tiếng Anh 1
Tiếng Anh 1 - Chứng chỉ Cambridge Pre A1 Starters
-
 Truyện cổ tích 1
Truyện cổ tích 1 - Truyện cổ tích
-
 Tự nhiên và xã hội 1
Tự nhiên và xã hội 1 - Tự nhiên & xã hội
- VBT Tự nhiên & xã hội
-
 Đạo đức 1
Đạo đức 1 - VBT Đạo Đức
- Giáo dục địa phương 1
- Tài liệu Giáo dục địa phương
-
- Công cụ
-
 Ngữ văn
Ngữ văn - Từ điển tiếng Việt
- Từ đồng nghĩa, trái nghĩa
- Thành ngữ Việt Nam
- Dẫn chứng nghị luận xã hội
- Ca dao, tục ngữ
- Chính tả tiếng Việt
- Từ láy
- Kho truyện
- >> Xem thêm
-
 Tiếng Anh
Tiếng Anh - Động từ bất quy tắc
- Cụm động từ (Phrasal verbs)
-

- PHẦN ĐẠI SỐ

-

 Chương 1: Mệnh đề - Tập hợp
Chương 1: Mệnh đề - Tập hợp - 100 bài tập mệnh đề
- 100 bài tập tập hợp
- 100 bài tập các phép toán trên tập hợp
- 100 bài tập các tập hợp số
-

 Chương 2: Hàm số bậc nhất và bậc hai
Chương 2: Hàm số bậc nhất và bậc hai - 100 bài tập hàm số
- 100 bài tập hàm số y=ax+b
- 100 bài tập hàm số bậc hai
-

 Chương 3: Phương trình - Hệ phương trình
Chương 3: Phương trình - Hệ phương trình - 200 bài tập phương trình
- 100 bài tập hệ phương trình
-

 Chương 4: Bất đẳng thức. Bất phương trình
Chương 4: Bất đẳng thức. Bất phương trình - 100 bài tập bất đẳng thức
- 100 bài tập bất phương trình
- 100 bài tập hệ bất phương trình
-

 Chương 6: Cung và góc lượng giác. Công thức lượng giác
Chương 6: Cung và góc lượng giác. Công thức lượng giác - 100 bài tập cung lượng giác và góc lượng giác
- 100 bài tập giá trị lượng giác của một cung
- 100 bài tập công thức lượng giác
-
- PHẦN HÌNH HỌC

-

 Chương 1: Vecto
Chương 1: Vecto - 100 bài tập các định nghĩa về vecto
- 100 bài tập tổng và hiệu của hai vecto
- 100 bài tập tích của một vecto với một số
- 100 bài tập hệ trục tọa độ
-

 Chương 2: Tích vô hướng và ứng dụng
Chương 2: Tích vô hướng và ứng dụng - 30 bài tập về Giá trị lượng giác của một góc bất kỳ từ 0 độ đến 180 độ
- 100 bài tập Tích vô hướng của hai vectơ
- 100 bài tập hệ thức lượng trong tam giác và giải tam giác
-

 Chương 3: Phương pháp tọa độ trong mặt phẳng
Chương 3: Phương pháp tọa độ trong mặt phẳng - 200 bài tập phương trình đường thẳng
- 100 bài tập phương trình đường tròn
- 80 bài tập phương trình đường elip
-

30 bài tập phương trình đường tròn mức độ thông hiểu
Làm đề thiCâu hỏi 1 :
Tâm I và bán kính R của đtròn (C): \(2{x^2} + 2{y^2} - 3x + 4y - 1 = 0\).
- A
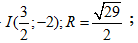
- B
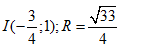
- C
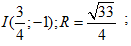
- D

Đáp án: C
Lời giải chi tiết:
\(\eqalign{ & 2{x^2} + 2{y^2} - 3x + 4y-1 = 0 \cr & \Rightarrow {x^2} + {y^2} - {3 \over 2}x + 2y-{1 \over 2} = 0 \cr & \Rightarrow {\left( {x - {3 \over 4}} \right)^2} + {\left( {y + 1} \right)^2} = {1 \over 2} + {9 \over {16}} + 1 = {{33} \over {16}} \cr & \Rightarrow I\left( {{3 \over 4}; - 1} \right);R = {{\sqrt {33} } \over 4} \cr} \)
Chọn C.
Đáp án - Lời giảiCâu hỏi 2 :
Trong các phương trình sau, phương trình nào biểu diễn đường tròn
- A x2+y2+2x-4y+9=0
- B x2+y2-6x+4y+13=0
- C 2x2+2y2-8x-4y-6=0
- D 5x2+4y2+x-4y+1=0
Đáp án: C
Lời giải chi tiết:

Câu hỏi 3 :
Có mấy phương trình đường tròn đi qua A(2;-1) tiếp xúc với hai trục tọa độ:
- A 0
- B 1
- C 2
- D 3
Đáp án: C
Lời giải chi tiết:
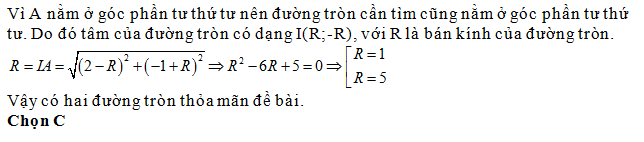
Câu hỏi 4 :
Với điều kiện nào thì \({{x}^{2}}+{{y}^{2}}+2ax+2by+c=0,\) biểu diễn phương trình đường tròn.
- A \({{a}^{2}}+{{b}^{2}}-c<0\)
- B \({{a}^{2}}+{{b}^{2}}\le c\)
- C \({{a}^{2}}+{{b}^{2}}\ge c\)
- D \({{a}^{2}}+{{b}^{2}}>c\)
Đáp án: D
Phương pháp giải:
Biến đổi tương đương\({{x}^{2}}+{{y}^{2}}+2ax+2by+c=0\Leftrightarrow {{\left( x+a \right)}^{2}}+{{\left( y+b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-c\)
Lời giải chi tiết:
\({{x}^{2}}+{{y}^{2}}+2ax+2by+c=0,\)là phương trình đường tròn khi \({{R}^{2}}={{a}^{2}}+{{b}^{2}}-c\). Điều này có nghĩa là \({{a}^{2}}+{{b}^{2}}-c>0\) hay \({{a}^{2}}+{{b}^{2}}>c\).
Chọn D.
Đáp án - Lời giảiCâu hỏi 5 :
Với điều kiện nào của \(m\) thì phương trình sau đây là phương trình đường tròn \({{x}^{2}}+{{y}^{2}}-2(m+2)x+4my+19m-6=0\) ?
- A \(1<m<2\)
- B \(-2\le m\le 1\)
- C \(m<1\) hoặc \(m>2\)
- D \(m<-2\) hoặc \(m>1\)
Đáp án: C
Phương pháp giải:
Biến đổi phương trình về dạng \({{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{R}^{2}}\), sử dụng điều kiện \({{R}^{2}}>0\)
Lời giải chi tiết:
\({{x}^{2}}+{{y}^{2}}-2\left( m+2 \right)x+4my+19m-6=0\,\,\,\,\left( * \right)\)
(*) là phương trình đường tròn khi \({{\left( m+2 \right)}^{2}}+{{\left( 2m \right)}^{2}}-19m+6>0\Leftrightarrow 5{{m}^{2}}-15m+10>0\)\(\Leftrightarrow \) \(m<1\) hoặc \(m>2\)
Chọn C.
Đáp án - Lời giảiCâu hỏi 6 :
Cho đường tròn\((C):{{x}^{2}}+{{y}^{2}}+2x+4y-20=0\). Tìm mệnh đề sai trong các mệnh đề sau:
- A \((C)\) có tâm \(I(1,2)\)
- B \((C)\) có bán kính \(R=5\)
- C \((C)\) đi qua điểm \(M(2,2)\)
- D \((C)\) không đi qua điểm \(A(1,1)\)
Đáp án: A
Phương pháp giải:
+) Phương trình đường tròn có dạng \({{x}^{2}}+{{y}^{2}}+2ax+2by+c=0\) với các hệ số \(a,b,c\) thỏa mãn điều kiện \({{a}^{2}}+{{b}^{2}}>c\)có tâm \(I(-a;-b)\)và bán kính \(R=\sqrt{{{a}^{2}}+{{b}^{2}}-c}\)
+) \((C)\) đi qua điểm \(M({{x}_{0}};{{y}_{0}})\) khi và chỉ khi \({{x}_{0}}^{2}+{{y}_{0}}^{2}+2a{{x}_{0}}+2b{{y}_{0}}+c=0\)
+) \((C)\) không đi qua điểm \(N({{x}_{0}};{{y}_{0}})\) khi và chỉ khi \({{x}_{0}}^{2}+{{y}_{0}}^{2}+2a{{x}_{0}}+2b{{y}_{0}}+c\ne 0\)
Lời giải chi tiết:
\((C):{{x}^{2}}+{{y}^{2}}+2x+4y-20=0\) có \(a=-1,\,\,b=-2,c=-20\) sẽ có tâm \(I\left( -1;-2 \right)\) và bán kính \(R=\sqrt{{{1}^{2}}+{{2}^{2}}+20}=5\). Suy ra mệnh đề sai là mệnh đề ở đáp án A.
Chọn A.
Đáp án - Lời giảiCâu hỏi 7 :
Cho hai điểm \(A(6;2)\) và \(B(-2;0)\) . Phương trình đường tròn (C) có đường kính AB là:
- A \({{(x-2)}^{2}}+{{(y-1)}^{2}}=17\)
- B \( {{(x-2)}^{2}}+{{(y-1)}^{2}}=2\sqrt{5}\)
- C \( {{(x-4)}^{2}}+{{(y-2)}^{2}}=17\)
- D \( {{(x+2)}^{2}}+{{(y+1)}^{2}}=17\)
Đáp án: A
Phương pháp giải:
Phương trình đường tròn (C) có đường kính AB có tâm I là trung điểm của AB và bán kính \(R=\frac{AB}{2}\). Sau đó áp dụng cách viết phương trình đường tròn có tâm tâm \(I(a;b)\) và bán kính \(R\) là: \({{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{R}^{2}}\)
Lời giải chi tiết:
Gọi I là trung điểm của AB.
Khi đó \(\left\{ \begin{array}{l}{x_I} = \frac{{{x_A} + {x_B}}}{2} = \frac{{6 - 2}}{2} = 2\\{y_I} = \frac{{{y_A} + {y_B}}}{2} = \frac{{2 + 0}}{2} = 1\end{array} \right. \Rightarrow I\left( {2;1} \right)\)
Mặt khác \(R=\frac{AB}{2}=\frac{\sqrt{{{\left( 6+2 \right)}^{2}}+{{\left( 2-0 \right)}^{2}}}}{2}=\frac{2\sqrt{17}}{2}=\sqrt{17}\)
Khi đó, (C) có dạng là: \({{\left( x-2 \right)}^{2}}+{{\left( y-1 \right)}^{2}}=17\).
Chọn A.
Đáp án - Lời giảiCâu hỏi 8 :
Phương trình đường tròn (C) đi qua hai điểm \(A(0;1),B(1;0)\) và có tâm nằm trên đường thẳng: \(x+y+2=0\) là:
- A \({{(x-1)}^{2}}+{{(y-1)}^{2}}=\sqrt{5}\)
- B \({{(x+1)}^{2}}+{{(y+1)}^{2}}=\sqrt{5}\)
- C \({{(x-1)}^{2}}+{{(y-1)}^{2}}=5\)
- D \({{(x+1)}^{2}}+{{(y+1)}^{2}}=5\)
Đáp án: D
Phương pháp giải:
Tìm điểm \(I({{x}_{I}};{{y}_{I}})\) nằm trên đường thẳng \(x+y+2=0\) và thỏa mãn điều kiện \(IA=IB\). Phương trình đường tròn (C) có tâm \(I({{x}_{I}};{{y}_{I}})\) và bán kính \(R=IA=IB\).
Lời giải chi tiết:
Giả sử điểm \(I({{x}_{I}};{{y}_{I}})\) là tâm của đường tròn (C). Vì I nằm trên đường thẳng \(x+y+2=0\) nên ta có \({{x}_{I}}+{{y}_{I}}+2=0\) (1)
Vì đường tròn (C) đi qua hai điểm \(A\left( 0;1 \right),\,\,B\left( 1;0 \right)\) nên ta có \(IA=IB\). Điều này tương đương với
\(I{{A}^{2}}=I{{B}^{2}}\) hay
\(\begin{array}{l}{\left( {{x_I}} \right)^2} + {\left( {1 - {y_I}} \right)^2} = {\left( {1 - {x_I}} \right)^2} + {\left( {{y_I}} \right)^2}\\ \Leftrightarrow x_I^2 + y_I^2 - 2{y_I} + 1 = x_I^2 - 2{x_I} + 1 + y_I^2\\ \Leftrightarrow {x_I} = {y_I}\,\,\,\,\left( 2 \right)\end{array}\)
Từ (1) và (2) suy ra \({{x}_{I}}={{y}_{I}}=-2\). Suy ra \(I\left( -1;-1 \right)\).
Mặt khác ta có \(R=IA=\sqrt{{{\left( -1 \right)}^{2}}+{{\left( -1-1 \right)}^{2}}}=\sqrt{5}\)
Vậy (C) có dạng \({{\left( x+1 \right)}^{2}}+{{\left( y+1 \right)}^{2}}=5\)
Chọn D
Đáp án - Lời giảiCâu hỏi 9 :
Phương trình đường tròn (C) đi qua 3 điểm \(A(0;2),\,\,\,B(-2;0)\) và \(C(2;0)\) là:
- A \( {{x}^{2}}+{{y}^{2}}=8\)
- B \( {{x}^{2}}+{{y}^{2}}+2x+4=0\)
- C \( {{x}^{2}}+{{y}^{2}}-2x-8=0\)
- D \( {{x}^{2}}+{{y}^{2}}-4=0\)
Đáp án: D
Phương pháp giải:
Thay trực tiếp tọa độ của 3 điểm vào phương trình trong mỗi đáp án.
Nếu xuất hiện một mệnh đề sai ở bước nào thì dừng lại và kết luận phương trình đó không qua 3 điểm A,B,C. Nếu có đủ 3 mệnh đề đúng thì kết luận phương trình đó qua 3 điểm A,B,C.
Lời giải chi tiết:
Cách làm:
A. \({{x}^{2}}+{{y}^{2}}=8\). Ta thay \(A(0;2)\) vào phương trình có \({{0}^{2}}+{{2}^{2}}=8\) là mệnh đề sai. Loại A
B. \({{x}^{2}}+{{y}^{2}}+2x+4=0\). Ta thay \(A(0;2)\) vào phương trình có \({{0}^{2}}+{{2}^{2}}+2.0+4=0\) là mệnh đề sai. Loại B
C. \({{x}^{2}}+{{y}^{2}}-2x-8=0\) Ta thay \(A(0;2)\) vào phương trình có \({{0}^{2}}+{{2}^{2}}-2.0-8=0\) là mệnh đề sai. Loại C.
Chọn D.
Đáp án - Lời giảiCâu hỏi 10 :
Phương trình đường tròn (C) có tâm \(I(6;-7)\) và tiếp xúc với đường thẳng Ox là:
- A \({{x}^{2}}+{{y}^{2}}-12x+14y+49=0\)
- B \({{x}^{2}}+{{y}^{2}}-12x+14y+36=0\)
- C \({{x}^{2}}+{{y}^{2}}-6x+7y-49=0\)
- D \({{x}^{2}}+{{y}^{2}}+6x-7y-36=0\)
Đáp án: B
Phương pháp giải:
\(\left( C \right)\) tiếp xúc \(\text{Ox}\Rightarrow R=d\left( I,\text{Ox} \right)\)
Lời giải chi tiết:
\(\left( C \right)\) tiếp xúc \(\text{Ox}\Rightarrow R=d\left( I,\text{Ox} \right)\). Mặt khác \(I\left( 6;-7 \right)\Rightarrow R=|-7|=7\)
\(\left( C \right)\) tâm \(I(6;-7),\,R=7\Rightarrow \left( C \right):{{\left( x-6 \right)}^{2}}+{{\left( y+7 \right)}^{2}}={{7}^{2}}\)
\(\begin{array}{l} \Leftrightarrow {x^2} - 12x + 36 + {y^2} + 14y + 49 = 49\\ \Leftrightarrow {x^2} + {y^2} - 12x + 14y + 36 = 0\end{array}\)
Chọn B.
Đáp án - Lời giảiCâu hỏi 11 :
Phương trình đường tròn (C) có tâm \(I(5;-2)\) và tiếp xúc với đường thẳng Oy là:
- A \({{x}^{2}}+{{y}^{2}}-10x+4y+4=0\)
- B \({{x}^{2}}+{{y}^{2}}-10x+4y+25=0\)
- C \({{x}^{2}}+{{y}^{2}}+10x-4y+4=0\)
- D \({{x}^{2}}+{{y}^{2}}+10x-4y+25=0\)
Đáp án: A
Phương pháp giải:
\(\left( C \right)\) tiếp xúc \(\text{Oy}\Rightarrow R=d\left( I,\text{Oy} \right)\)
Lời giải chi tiết:
\(\left( C \right)\) tiếp xúc \(\text{Oy}\Rightarrow R=d\left( I,\text{Oy} \right)\). Mặt khác \(I\left( 5;-2 \right)\Rightarrow R=\left| 5 \right|=5\)
\(\left( C \right)\) tâm \(I(5;-2),\,R=5\Rightarrow \left( C \right):{{\left( x-5 \right)}^{2}}+{{\left( y+2 \right)}^{2}}={{5}^{2}}\)
\(\begin{array}{l} \Leftrightarrow {x^2} - 10x + 25 + {y^2} + 4y + 4 = 25\\ \Leftrightarrow {x^2} + {y^2} - 10x + 4y + 4 = 0\end{array}\)
Chọn A.
Đáp án - Lời giảiCâu hỏi 12 :
Phương trình đường tròn (C) có tâm \(I(-2;2)\) và tiếp xúc với đường thẳng (d): \(x+2y+1=0\) là:
- A \({{x}^{2}}+{{y}^{2}}-4x+4y+\frac{49}{5}=0\)
- B \({{x}^{2}}+{{y}^{2}}+4x-4y+\frac{31}{5}=0\)
- C \({{x}^{2}}+{{y}^{2}}-4x+4y-\frac{31}{5}=0\)
- D \({{x}^{2}}+{{y}^{2}}+4x-4y+\frac{49}{5}=0\)
Đáp án: B
Phương pháp giải:
Đường tròn (C) tiếp xúc với đường thẳng \(\Delta :\)khi ta có \(d\left( I;\Delta \right)=R\)
Áp dụng công thức tính khoảng cách từ điểm \(I({{x}_{0}};{{y}_{0}})\) đến \(\Delta :\,\,ax+by+c=0\) là: \(d\left( I;\Delta \right)=\frac{\left| \text{a}{{\text{x}}_{0}}+b{{y}_{0}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}\)
Lời giải chi tiết:
\(\left( C \right)\) tiếp xúc \(d\Rightarrow R=d(I,d)=\frac{|-2+2.2+1|}{\sqrt{{{1}^{2}}+{{2}^{2}}}}=\frac{3}{\sqrt{5}}\)
\(\left( C \right)\) tâm \(I\left( -2;2 \right),\,R=\frac{3}{\sqrt{5}}\Rightarrow \left( C \right):{{(x+2)}^{2}}+{{\left( y-2 \right)}^{2}}=\frac{9}{5}\)
\(\begin{array}{l} \Leftrightarrow {x^2} + 4x + 4 + {y^2} - 4y + 4 = \frac{9}{5}\\ \Leftrightarrow {x^2} + {y^2} + 4x - 4y + \frac{{31}}{5} = 0\end{array}\)
Chọn B.
Đáp án - Lời giảiCâu hỏi 13 :
Trong mặt phẳng với hệ tọa độ Oxy, cho \(d:x-7y+10=0\) . Viết phương trình đường tròn có tâm thuộc đường thẳng \(\Delta :2x+y=0\) và tiếp xúc với đường thẳng d tại \(A(4;2)\) .
- A \({{(x-6)}^{2}}+{{(y+12)}^{2}}=100\)
- B \({{(x+6)}^{2}}+{{(y-12)}^{2}}=100\)
- C \({{(x+6)}^{2}}+{{(y-12)}^{2}}=200\)
- D \({{(x-6)}^{2}}+{{(y+12)}^{2}}=200\)
Đáp án: D
Phương pháp giải:
Giả sử đường tròn tâm I, bán kính R. Sử dụng tính chất:
Đường tròn tiếp xúc với đường thẳng d tại A nên ta có: \(\left\{ \begin{array}{l}\overrightarrow {AI} .\overrightarrow {{u_d}} = 0\\R = AI\end{array} \right.\).
Lời giải chi tiết:
Đường tròn có tâm thuộc đường thẳng \(\Delta :2x+y=0\) , giả sử \(I(i;-2i)\).
Vì đường tròn tiếp xúc với đường thẳng \(d:x-7y+10=0\) tại \(A(4;2)\) nên ta có: \(\left\{ \begin{array}{l}\overrightarrow {AI} .\overrightarrow {{u_d}} = 0\\R = AI\end{array} \right.\).
Mà \(\overrightarrow{AI}=\left( i-4;-2i-2 \right),\overrightarrow{{{u}_{d}}}=\left( 7;1 \right)\) nên ta có
\(7(i-4)+1.(-2i-2)=0\Leftrightarrow 5i-30=0\Leftrightarrow i=6\Rightarrow I(6;-12)\)
Và \(\overrightarrow{AI}=\left( 2;-14 \right)\Rightarrow R=AI=\sqrt{{{2}^{2}}+{{\left( -14 \right)}^{2}}}=10\sqrt{2}\).
Vậy ta có phương trình \({{\left( x-6 \right)}^{2}}+{{\left( y+12 \right)}^{2}}=200\)
Chọn D.
Đáp án - Lời giảiCâu hỏi 14 :
Phương trình đường tròn \((C)\) đi qua \(A(3;3)\) và tiếp xúc với đường thẳng \((d):2x+y-3=0\) tại điểm \(B(1;1)\) là:
- A \({{\left( x-\frac{7}{3} \right)}^{2}}+{{\left( y-\frac{5}{3} \right)}^{2}}=\frac{20}{9}\)
- B \({{\left( x+\frac{7}{3} \right)}^{2}}+{{\left( y+\frac{5}{3} \right)}^{2}}=\frac{20}{9}\)
- C \({{\left( x-\frac{5}{3} \right)}^{2}}+{{\left( y-\frac{7}{3} \right)}^{2}}=\frac{20}{9}\)
- D \({{\left( x+\frac{5}{3} \right)}^{2}}+{{\left( y+\frac{7}{3} \right)}^{2}}=\frac{20}{9}\)
Đáp án: A
Phương pháp giải:
Giả sử đường tròn có tâm I và bán kính R. Sử dụng tính chất:
đường tròn tiếp xúc với đường thẳng d tại B nên ta có: \(\overrightarrow{BI}.\overrightarrow{{{u}_{d}}}=0\). đường tròn qua A nên ta có \(R=IA=IB\).Lời giải chi tiết:
Giả sử đường tròn có tâm \(I(a;b)\)
Vì đường tròn tiếp xúc với đường thẳng \((d):2x+y-3=0\) tại \(B(1;1)\) nên ta có: \(\overrightarrow{BI}.\overrightarrow{{{u}_{d}}}=0\).
Mà \(\overrightarrow{BI}=\left( a-1;b-1 \right),\overrightarrow{{{u}_{d}}}=(1;-2)\) nên ta có
\(1\left( a-1 \right)-2\left( b-1 \right)=0\Leftrightarrow a-2b+1=0\,\,\,\,\left( 1 \right)\)
Vì đường tròn qua \(A\left( 3;3 \right)\) nên ta có \(R=IA=IB\)
\(IA=IB\Leftrightarrow {{\left( a-3 \right)}^{2}}+{{\left( b-3 \right)}^{2}}={{\left( a-1 \right)}^{2}}+{{\left( b-1 \right)}^{2}}\Leftrightarrow -4a-4b+16=0\Leftrightarrow a+b=4\,\,\,\left( 2 \right)\)
Từ (1) và (2) ta có hệ \(\left\{ \begin{array}{l}a - 2b + 1 = 0\\a + b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{7}{3}\\b = \frac{5}{3}\end{array} \right. \Rightarrow I\left( {\frac{7}{3};\frac{5}{3}} \right)\)
Ta có \(R=BI=\sqrt{{{\left( \frac{7}{3}-1 \right)}^{2}}+{{\left( \frac{5}{3}-1 \right)}^{2}}}=\sqrt{\frac{20}{9}}\)
Vậy ta có phương trình \({{\left( x-\frac{7}{3} \right)}^{2}}+{{\left( y-\frac{5}{3} \right)}^{2}}=\frac{20}{9}\)
Chọn A.
Đáp án - Lời giảiCâu hỏi 15 :
Phương trình đường tròn (C) có bán kính bằng 5, tiếp xúc với đường thẳng \(\Delta :\)\(3x+4y-20=0\) , có tâm \(I({{x}_{I}}>0)\) nằm trên đường thẳng \(d:\) \(x+y+1=0\) .
- A \(\left( C \right):{{\left( x-41 \right)}^{2}}+{{\left( y+42 \right)}^{2}}=25\)
- B \(\left( C \right):{{\left( x+41 \right)}^{2}}+{{\left( y-42 \right)}^{2}}=25\)
- C \(\left( C \right):{{\left( x-1 \right)}^{2}}+{{\left( y+2 \right)}^{2}}=25\)
- D \(\left( C \right):{{\left( x+9 \right)}^{2}}+{{\left( y-10 \right)}^{2}}=25\)
Đáp án: C
Phương pháp giải:
Đường tròn (C) tiếp xúc với đường thẳng \(\Delta :\) khi ta có \(d(I;\Delta )=R\)
Áp dụng công thức tính khoảng cách từ điểm \(I({{x}_{0}};{{y}_{0}})\) đến \(\Delta :\,\,ax+by+c=0\) là \(d\left( I;\Delta \right)=\frac{\left| \text{a}{{\text{x}}_{0}}+b{{y}_{0}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}\)
Lời giải chi tiết:
Giả sử \(I(a;b)\) là tâm của đường tròn (C) với \(a>0\)
Theo giả thiết \(I(a;b)\) nằm trên đường thẳng \(d:\)\(x+y+1=0\) nên ta có \(I(a;-1-a)\).
Vì đường tròn (C) có bán kính bằng 5, tiếp xúc với đường thẳng \(\Delta :\)\(3x+4y-20=0\) nên ta có
\(d(I;\Delta )=R\) \(\frac{{\left| {3.a + 4\left( { - 1 - a} \right) - 20} \right|}}{{\sqrt {{3^2} + {4^2}} }} = 5 \Leftrightarrow \left| { - a - 24} \right| = 25 \Leftrightarrow \left[ \begin{array}{l} - a - 24 = 25\\ - a - 24 = - 25\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}a = - 49\\a = 1\end{array} \right.\)
Vì \(a>0\) nên chọn a = 1.
\((C)\) có tâm \(I\left( 1;-2 \right)\) và \(R=5\)\(\Rightarrow (C):{{\left( x-1 \right)}^{2}}+{{\left( y+2 \right)}^{2}}=25\)
Chọn C.
Đáp án - Lời giảiCâu hỏi 16 :
Phương trình đường tròn đường kính AB, biết \(A(1;1),\,\,B(3;5)\) là:
- A \({x^2} + {y^2} - 4x - 6y + 8 = 0\).
- B \({x^2} + {y^2} + 4x + 6y - 12 = 0\).
- C \({x^2} + {y^2} - 4x + 6y + 8 = 0\).
- D \({x^2} + {y^2} + 4x - 6y + 8 = 0\).
Đáp án: A
Phương pháp giải:
Đường tròn đường kính AB có tâm I là trung điểm của AB, bán kính \(R = \frac{{AB}}{2}\).
Lời giải chi tiết:
Tọa độ trung điểm I của AB: \(\left\{ \begin{array}{l}{x_I} = \frac{{{x_A} + {x_B}}}{2}\\{y_I} = \frac{{{y_A} + {y_B}}}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_I} = \frac{{1 + 3}}{2}\\{y_I} = \frac{{1 + 5}}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_I} = 2\\{y_I} = 3\end{array} \right. \Rightarrow I(2;3)\)
\(R = \frac{{AB}}{2} = \frac{{\sqrt {{{(3 - 1)}^2} + {{(5 - 1)}^2}} }}{2} = \sqrt 5 \)
Phương trình đường tròn đường kính AB: \({(x - 2)^2} + {(y - 3)^2} = 5 \Leftrightarrow {x^2} + {y^2} - 4x - 6y + 8 = 0\)
Chọn: A
Đáp án - Lời giảiCâu hỏi 17 :
Tìm giao điểm của hai đường tròn \(\left( {{C_1}} \right):\,\,{x^2} + {y^2} - 2 = 0\) và \(\left( {{C_2}} \right):{x^2} + {y^2} - 2x = 0\).
- A (2;0) và (0;2).
- B \(\left( {\sqrt 2 ;1} \right)\) và \(\left( {1; - \sqrt 2 } \right)\).
- C \(\left( {1; - 1} \right)\) và \(\left( {1;1} \right)\).
- D \(\left( { - 1;0} \right)\) và \(\left( {0; - 1} \right)\).
Đáp án: C
Phương pháp giải:
Giải hệ phương trình tọa độ giao điểm: \(\left\{ \begin{array}{l}{x^2} + {y^2} - 2 = 0\\{x^2} + {y^2} - 2x = 0\end{array} \right.\)
Lời giải chi tiết:
Tọa độ giao điểm của hai đường tròn \(\left( {{C_1}} \right):\,\,{x^2} + {y^2} - 2 = 0\) và \(\left( {{C_2}} \right):{x^2} + {y^2} - 2x = 0\) là nghiệm của hệ phương trình: \(\left\{ \begin{array}{l}{x^2} + {y^2} - 2 = 0\\{x^2} + {y^2} - 2x = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x^2} + {y^2} - 2 = 0\\2 - 2x = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{1^2} + {y^2} - 2 = 0\\x = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}y = 1\\y = - 1\end{array} \right.\\x = 1\end{array} \right.\)
Vậy, tọa độ 2 giao điểm là \(\left( {1; - 1} \right)\) và \(\left( {1;1} \right)\).
Chọn: C
Đáp án - Lời giảiCâu hỏi 18 :
Cho đường tròn (C) có tâm \(I\left( {2;1} \right)\) và tiếp xúc với đường thẳng \(\left( \Delta \right):\,\,2x + y + 4 = 0\) có phương trình là:
- A \({\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = 5\)
- B \({\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = 81\)
- C \({\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = \frac{{18}}{5}\)
- D \({\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = \frac{{81}}{5}\)
Đáp án: D
Lời giải chi tiết:
+) Ta có: \(R = d\left( {I;\Delta } \right) = \frac{{\left| {2.2 + 1 + 4} \right|}}{{\sqrt {{2^2} + {1^2}} }} = \frac{9}{{\sqrt 5 }}\)
+) Phương trình đường tròn (C) là: \({\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = \frac{{81}}{5}\) .
Chọn D.
Đáp án - Lời giảiCâu hỏi 19 :
Trong mặt phẳng \(Oxy\), đường tròn \(\left( C \right):{x^2} + {y^2} + 4x + 6y - 12 = 0\) có tâm là:
- A \(I\left( { - 2; - 3} \right).\)
- B \(I\left( { - 2; - 3} \right).\)
- C \(I\left( {4;6} \right).\)
- D \(I\left( { - 4; - 6} \right).\)
Đáp án: A
Phương pháp giải:
Đường tròn \({x^2} + {y^2} - 2ax - 2by + c = 0\) có tâm \(I\left( {a;b} \right)\), bán kính \(R = \sqrt {{a^2} + {b^2} - c} \)
Lời giải chi tiết:
Đường tròn \(\left( C \right):{x^2} + {y^2} + 4x + 6y - 12 = 0\) có tâm \(I\left( { - 2; - 3} \right)\)
Chọn A.
Đáp án - Lời giảiCâu hỏi 20 :
Một đường tròn có tâm \(I\left( {3;4} \right)\) tiếp xúc với đường thẳng \(\Delta :3x + 4y - 10 = 0\). Hỏi bán kính đường tròn bằng bao nhiêu?
- A \(\frac{5}{3}\)
- B \(5\)
- C \(3\)
- D \(\frac{3}{5}\)
Đáp án: C
Phương pháp giải:
Đường thẳng \(\Delta \) là tiếp xúc với đường tròn \(\left( {O,R} \right) \Leftrightarrow d\left( {O,\Delta } \right) = R\)
Lời giải chi tiết:
Đường tròn có tâm \(I\left( {3;4} \right)\) tiếp xúc với đường thẳng \(\Delta :3x + 4y - 10 = 0\)
\( \Leftrightarrow R = d\left( {I,\Delta } \right) = \frac{{\left| {3.3 + 4.4 - 10} \right|}}{{\sqrt {{3^2} + {4^2}} }} = \frac{{15}}{5} = 3\)
Chọn C.
Đáp án - Lời giảiCâu hỏi 21 :
Cho đường tròn \(\left( C \right):{x^2} + {y^2} - 2x - 4y - 4 = 0\) và điểm \(A\left( {1;5} \right)\). Đường thẳng nào trong các đường thẳng dưới đây là tiếp tuyến của đường tròn \(\left( C \right)\) tại A?
- A \(y - 5 = 0\).
- B \(y + 5 = 0\).
- C \(x + y - 5 = 0\).
- D \(x - y - 5 = 0\).
Đáp án: A
Phương pháp giải:
Đường thẳng \(\Delta \) tiếp xúc với đường tròn \(\left( {O,R} \right)\) tại \(A \in \left( {O,R} \right)\)\( \Leftrightarrow OA \bot \Delta \) tại A
Lời giải chi tiết:
Đường tròn \(\left( C \right)\) có tâm \(O\left( {1;2} \right)\) và bán kính \(R = 3.\)
Gọi \(\Delta \) là tiếp tuyến của \(\left( C \right)\) tại A
Ta có: \(\overrightarrow {OA} = \left( {0;3} \right)\) là một VTCP của \(\Delta \)
Phương trình \(\Delta \): \(0.\left( {x - 1} \right) + 3\left( {y - 5} \right) = 0 \Leftrightarrow y - 5 = 0\)
Chọn A.
Đáp án - Lời giảiCâu hỏi 22 :
Trong mặt phẳng với hệ tọa độ \(Oxy\), lập phương trình đường tròn \((C)\) có tâm \(I\left( {2; - 3} \right)\)và có bán kính \(R = 4\).
- A \({\left( {x + 2} \right)^2} + {\left( {y - 3} \right)^2} = 16\).
- B \({\left( {x + 2} \right)^2} + {\left( {y - 3} \right)^2} = 4\).
- C \({\left( {x - 2} \right)^2} + {\left( {y + 3} \right)^2} = 4\).
- D \({\left( {x - 2} \right)^2} + {\left( {y + 3} \right)^2} = 16\).
Đáp án: D
Phương pháp giải:
Đường tròn \(\left( C \right):{\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = c\) có tâm \(I\left( {a;b} \right)\), bán kính \(R = \sqrt c \)
Lời giải chi tiết:
Phương trình đường tròn \((C)\) có tâm \(I\left( {2; - 3} \right)\) và có bán kính \(R = 4\) là \({\left( {x - 2} \right)^2} + {\left( {y + 3} \right)^2} = 16\)
Chọn D.
Đáp án - Lời giảiCâu hỏi 23 :
Trong mặt phẳng với hệ tọa độ \(Oxy\), cho đường tròn \((C):{\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 4\). Khẳng định nào đúng ?
- A Đường tròn \(\left( C \right)\) cắt trục \(Ox\) tại hai điểm phân biệt.
- B Đường tròn \(\left( C \right)\) có bán kính \(R = 4\).
- C Đường tròn \(\left( C \right)\) có tâm \(I\left( {1; - 2} \right)\).
- D Đường tròn \(\left( C \right)\) cắt trục \(Oy\) tại hai điểm phân biệt.
Đáp án: D
Phương pháp giải:
Đường tròn \(\left( C \right):{\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = c\) có tâm \(I\left( {a;b} \right)\), bán kính \(R = \sqrt c \)
Lời giải chi tiết:
Đường tròn \((C):{\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 4\) có tâm \(I\left( { - 1;2} \right)\), bán kính \(R = 2\)
Dễ thấy \(d\left( {I,Oy} \right) = 1 < 2 = R\) nên đường tròn \(\left( C \right)\) cắt trục \(Oy\) tại hai điểm phân biệt.
Chọn D.
Đáp án - Lời giảiCâu hỏi 24 :
Trong mặt phẳng với hệ tọa độ \(Oxy\), đường tròn tâm \(I\left( {1;3} \right)\) tiếp xúc với đường thẳng \(\Delta :3x + 4y = 0\) thì có bán kính bằng bao nhiêu ?
- A \(3\)
- B \(\frac{3}{5}.\)
- C \(1\)
- D \(15\)
Đáp án: A
Phương pháp giải:
Đường thẳng \(\Delta \) là tiếp tuyến của đường tròn \(\left( {O;R} \right) \Leftrightarrow d\left( {O,\Delta } \right) = R\)
Lời giải chi tiết:
Đường tròn tâm \(I\left( {1;3} \right)\) tiếp xúc với đường thẳng \(\Delta :3x + 4y = 0\)
\( \Leftrightarrow R = d\left( {I,\Delta } \right) = \frac{{\left| {3.1 + 4.3} \right|}}{{\sqrt {{3^2} + {4^2}} }} = \frac{{15}}{5} = 3\)
Chọn A.
Đáp án - Lời giảiCâu hỏi 25 :
Với những giá trị nào của m thì đường thẳng \(\Delta :3x - 4y + m - 1 = 0\) tiếp xúc đường tròn \(\left( C \right):\,\,{x^2} + {y^2} - 16 = 0\)
- A \(m = 19\)và\(m = - 21\)
- B \(m = - 19\)và\(m = - 21\)
- C \(m = 19\)và\(m = 21\)
- D \(m = - 19\)và\(m = 21\)
Đáp án: D
Phương pháp giải:
Đường thẳng \(\Delta \) tiếp xúc với đường tròn \(\left( C \right)\) tâm I bán kính R \( \Leftrightarrow d\left( {I;\Delta } \right) = R.\)
Cho đường thẳng \(\Delta :ax + by + c = 0\) và điểm \({M_0}\left( {{x_0};{y_0}} \right) \Rightarrow d\left( {{M_0};\Delta } \right) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}.\)
Lời giải chi tiết:
Đường tròn \(\left( C \right)\) có tâm \(I\left( {0;0} \right)\) bán kính \(R = \sqrt {0 + 0 + 16} = 4\)
Đường thẳng \(\Delta \) tiếp xúc với đường tròn \(\left( C \right)\)\( \Leftrightarrow d\left( {I;\Delta } \right) = R\)
\( \Leftrightarrow \frac{{\left| {m - 1} \right|}}{{\sqrt {{3^2} + {4^2}} }} = 4 \Leftrightarrow \left| {m - 1} \right| = 20 \Leftrightarrow \left[ \begin{array}{l}m - 1 = 20\\m - 1 = - 20\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 21\\m = - 19\end{array} \right.\)
Chọn D.
Đáp án - Lời giảiCâu hỏi 26 :
Tìm tất cả các giá trị của tham số \(m\) để phương trình \({x^2} + {y^2} + 2mx - 4\left( {m + 1} \right)y + 4{m^2} + 5m + 2 = 0\)
là phương trình của một đường tròn trong mặt phẳng tọa độ Oxy.
- A \( - 2 < m < - 1\)
- B \(\left[ \begin{array}{l}m < 1\\m > 2\end{array} \right.\)
- C \(\left[ \begin{array}{l}m < - 2\\m > - 1\end{array} \right.\)
- D \(\left[ \begin{array}{l}m \le - 2\\m \ge - 1\end{array} \right.\)
Đáp án: C
Phương pháp giải:
Phương trình \({x^2} + {y^2} - 2ax - 2by + c = 0\) là phương trình đường tròn \( \Leftrightarrow {a^2} + {b^2} - c > 0\).
Lời giải chi tiết:
\({x^2} + {y^2} + 2mx - 4\left( {m + 1} \right)y + 4{m^2} + 5m + 2 = 0\,\,\,\left( 1 \right)\)
Có \(a = - m,\,\,b = 2\left( {m + 1} \right),\) \(c = 4{m^2} + 5m + 2\)
(1) là phương trình đường tròn \( \Leftrightarrow {a^2} + {b^2} - c > 0\)
\(\begin{array}{l} \Leftrightarrow {\left( { - m} \right)^2} + 4{\left( {m + 1} \right)^2} - \left( {4{m^2} + 5m + 2} \right) > 0\\ \Leftrightarrow {m^2} + 4\left( {{m^2} + 2m + 1} \right) - 4{m^2} - 5m - 2 > 0\\ \Leftrightarrow {m^2} + 4{m^2} + 8m + 4 - 4{m^2} - 5m - 2 > 0\\ \Leftrightarrow {m^2} + 3m + 2 > 0\\ \Leftrightarrow \left( {m + 1} \right)\left( {m + 2} \right) > 0\\ \Leftrightarrow \left[ \begin{array}{l}m > - 1\\m < - 2\end{array} \right.\end{array}\)
Chọn C.
Đáp án - Lời giảiCâu hỏi 27 :
Cho đường tròn \(\left( C \right):\,\,{x^2} + {y^2} - 4x - 2y = 0\) và đường thẳng \(\Delta :\,\,x + 2y + 1 = 0\). Tìm mệnh đề đúng trong các mệnh đề sau:
- A \(\Delta \)đi qua tâm của \(\left( C \right)\)
- B \(\Delta \) cắt \(\left( C \right)\) tại hai điểm
- C \(\Delta \) tiếp xúc với \(\left( C \right)\)
- D \(\Delta \)không có điểm chung với \(\left( C \right)\)
Đáp án: C
Phương pháp giải:
Cách 1: Xác định tọa độ giao điểm của đường tròn \(\left( C \right)\) và đường thẳng \(\left( \Delta \right)\)
Cách 2: So sánh khoảng cách từ tâm đường tròn \(\left( C \right)\) đến đường thẳng \(\left( \Delta \right)\) với \(R\)
Lời giải chi tiết:
Đường tròn \(\left( C \right):\,\,{x^2} + {y^2} - 4x - 2y = 0\) có tọa độ tâm \(I\left( {2;\,\,1} \right)\) và \(R = \sqrt 5 \)
Thay \(I\left( {2;\,\,1} \right)\) vào \(\Delta :\,\,x + 2y + 1 = 0\) ta được: \(2 + 2.1 + 1 = 5 \ne 0\)
\( \Rightarrow I\left( {2;\,\,1} \right) \notin \left( \Delta \right)\)
\( \Rightarrow \Delta \) không đi qua tâm của \(\left( C \right)\)
Tọa độ giao điểm của \(\Delta \) và \(\left( C \right)\) là nghiệm của hệ phương trình:
\(\left\{ \begin{array}{l}{x^2} + {y^2} - 4x - 2y = 0\\x + 2y + 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x^2} + {y^2} - 4x - 2y = 0\\x = - 2y - 1\end{array} \right.\)
\( \Rightarrow {\left( { - 2y - 1} \right)^2} + {y^2} - 4.\left( { - 2y - 1} \right) - 2y = 0\)
\( \Leftrightarrow 4{y^2} + 4y + 1 + {y^2} + 8y + 4 - 2y = 0\)
\( \Leftrightarrow 5{y^2} + 10y + 5 = 0\)
\( \Leftrightarrow y = - 1\)
Với \(y = - 1 \Rightarrow x = 1\)
Vậy tọa độ giao điểm của \(\Delta \) và \(\left( C \right)\) là \(\left( {1;\,\, - 1} \right)\).
Vậy \(\Delta \) tiếp xúc với \(\left( C \right)\).
Chọn C
Đáp án - Lời giảiCâu hỏi 28 :
Đường tròn \(\left( C \right):\,\,{(x - 2)^2} + {(y - 1)^2} = 25\) không cắt đường thẳng nào trong các đường thẳng sau đây?
- A Đường thẳng đi qua điểm \(\left( {2;\,\,6} \right)\) và điểm \(\left( {45;\,\,50} \right)\)
- B Đường thẳng có phương trình \(y-4 = 0\)
- C Đường thẳng đi qua điểm \(\left( {3;\,\, - 2} \right)\) và điểm \(\left( {19;\,\,33} \right)\)
- D Đường thẳng có phương trình \(x - 8 = 0\)
Đáp án: D
Phương pháp giải:
+) Viết phương trình đường thẳng \(\left( \Delta \right)\) đi qua hai điểm đã cho.
+) So sánh khoảng cách từ tâm của đường tròn \(\left( C \right)\) đến đường thẳng \(\left( \Delta \right)\) với bán kính.
(Để đường tròn \(\left( C \right)\) không cắt đường thẳng \(\left( \Delta \right)\) thì khoảng cách từ tâm của đường tròn \(\left( C \right)\) đến đường thẳn \(\left( \Delta \right)\) lớn hơn bán kính)
Lời giải chi tiết:
\(\left( C \right):\,\,{\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = 25 \Rightarrow \left\{ \begin{array}{l}I\left( {2;\,\,1} \right)\\R = 5\end{array} \right.\)
Phương trình đường thẳng đi qua hai điểm \(\left( {2;\,\,6} \right)\) và \(\left( {45;\,\,50} \right)\) là:
\(\frac{{x - 2}}{{43}} = \frac{{y - 6}}{{44}} \Leftrightarrow 44\,.\left( {x - 2} \right) = 43.\left( {y - 6} \right) \Leftrightarrow 44x - 88 = 43y - 258 \Leftrightarrow 44x - 43y + 170 = 0\)
Phương trình đường thẳng đi qua hai điểm \(\left( {3;\, - 2} \right)\) và \(\left( {19;\,\,33} \right)\) là :
\(\frac{{x - 3}}{{16}} = \frac{{y + 2}}{{35}} \Leftrightarrow 35\left( {x - 3} \right) = 16\left( {y + 2} \right) \Leftrightarrow 35x - 105 = 16y + 32 \Leftrightarrow 35x - 16y - 137 = 0\)
Khoảng cách từ tâm đến các đường thẳng là:
\({d_A} = \frac{{215}}{{\sqrt {3785} }} < R;\,\,\,{d_B} = 3 < R;\,\,\,{d_C} = \frac{{19}}{{\sqrt {1481} }} < R;\,\,{d_D} = 6 > R\)
Chọn D
Đáp án - Lời giảiCâu hỏi 29 :
Trong mặt phẳng tọa độ Oxy, cho hai điểm \(A(1;3)\)và \(B( - 3;5)\). Phương trình nào dưới đây là phương trình của đường tròn đường kính \(AB\)?
- A \({\left( {x - 1} \right)^2} + {\left( {y + 4} \right)^2} = 5\)
- B \({\left( {x - 1} \right)^2} + {\left( {y + 4} \right)^2} = 25\)
- C \({\left( {x + 1} \right)^2} + {\left( {y - 4} \right)^2} = 25\)
- D \({\left( {x + 1} \right)^2} + {\left( {y - 4} \right)^2} = 5\)
Đáp án: D
Phương pháp giải:
Đường tròn đường kính AB có tâm là trung điểm AB và bán kính \(R = \frac{{AB}}{2}\).
Công thức viết phương trình đường tròn biết tâm \(I\left( {a;b} \right)\) bán kính \(R\) là: \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}\)
Lời giải chi tiết:
Gọi I là trung điểm của AB. Khi đó \(\left\{ \begin{array}{l}{x_I} = \frac{{{x_A} + {x_B}}}{2}\\{y_I} = \frac{{{y_A} + {y_B}}}{2}\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}{x_I} = \frac{{1 + \left( { - 3} \right)}}{2} = - 1\\{y_I} = \frac{{3 + 5}}{2} = 4\end{array} \right.\) \( \Rightarrow I\left( { - 1;4} \right)\)
Ta có: \(AB = \sqrt {{{\left( { - 3 - 1} \right)}^2} + {{\left( {5 - 3} \right)}^2}} \) \( = 2\sqrt 5 \)
Đường tròn đường kính AB có tâm \(I\left( { - 1;4} \right)\) bán kính \(R = \frac{{AB}}{2} = \frac{{2\sqrt 5 }}{2} = \sqrt 5 \) nên có phương trình:
\({\left( {x + 1} \right)^2} + {\left( {y - 4} \right)^2} = {\left( {\sqrt 5 } \right)^2}\)\( \Leftrightarrow {\left( {x + 1} \right)^2} + {\left( {y - 4} \right)^2} = 5\)
Chọn D.
Đáp án - Lời giảiCâu hỏi 30 :
Đường tròn tâm \(\left( C \right)\) có tâm \(I\left( {1; - 5} \right)\) và bán kính \(R = 2\sqrt 3 \) có phương trình là
- A \({\left( {x - 1} \right)^2} + {\left( {y + 5} \right)^2} = 12\).
- B \({\left( {x - 1} \right)^2} + {\left( {y + 5} \right)^2} = 18\).
- C \({\left( {x + 1} \right)^2} + {\left( {y - 5} \right)^2} = 18\).
- D \({\left( {x + 1} \right)^2} + {\left( {y - 5} \right)^2} = 12\).
Đáp án: A
Phương pháp giải:
Phương trình đường tròn tâm \(I\left( {a;\,\,b} \right)\) và bán kính \(R\) là \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}.\)
Lời giải chi tiết:
Phương trình đường tròn tâm \(I\left( {1; - 5} \right)\) và bán kính \(R = 2\sqrt 3 \) là \({\left( {x - 1} \right)^2} + {\left( {y + 5} \right)^2} = 12\)
Chọn A.
Đáp án - Lời giảiXem thêm
40 bài tập phương trình đường tròn mức độ vận dụng, vận dụng caoTổng hợp các bài tập trắc nghiệm phương trình đường tròn mức độ vận dụng, vận dụng cao có đáp án và lời giải chi tiết
Xem chi tiết 30 bài tập phương trình đường tròn mức độ nhận biếtTổng hợp các bài tập trắc nghiệm phương trình đường tròn mức độ nhận biết có đáp án và lời giải chi tiết
Xem chi tiết>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
 |  |  |  |
 |  |  |  |
Các bài khác cùng chuyên mục
- 25 bài tập phương trình đường elip mức độ vận dụng, vận dụng cao
- 30 bài tập phương trình đường elip mức độ thông hiểu
- 25 bài tập phương trình đường elip mức độ nhận biết
- 40 bài tập phương trình đường tròn mức độ vận dụng, vận dụng cao
- 30 bài tập phương trình đường tròn mức độ thông hiểu
- 25 bài tập phương trình đường elip mức độ vận dụng, vận dụng cao
- 30 bài tập phương trình đường elip mức độ thông hiểu
- 25 bài tập phương trình đường elip mức độ nhận biết
- 40 bài tập phương trình đường tròn mức độ vận dụng, vận dụng cao
- 30 bài tập phương trình đường tròn mức độ thông hiểu
Báo lỗi góp ý
Vấn đề em gặp phải là gì ?Sai chính tả
Giải khó hiểu
Giải sai
Lỗi khác
Hãy viết chi tiết giúp Loigiaihay.com
Gửi góp ý Hủy bỏ Liên hệ Chính sáchCopyright © 2021 loigiaihay.com






Từ khóa » Bài Tập Tự Luận Phương Trình đường Tròn Lớp 10
-
Các Dạng Bài Tập Toán Về Phương Trình đường Tròn - Toán Lớp 10
-
Bài Tập Phương Trình đường Tròn Lớp 10 Cực Hay - TÀI LIỆU RẺ
-
Các Dạng Bài Tập Về Phương Trình đường Tròn - Toán 10
-
Phương Trình đường Tròn: Lý Thuyết Và Các Dạng Bài Tập Chuyên đề ...
-
Phương Trình đường Tròn Và Các Dạng Bài Tập Có Lời Chuẩn 100%
-
Chuyên đề Phương Trình đường Tròn Dạng Toán Và Bài Tập - 123doc
-
Phương Trình đường Tròn - Bài Tập Toán Lớp 10 - Itoan
-
Phương Trình đường Tròn Lớp 10 Chuẩn Nhất - CungHocVui
-
Chuyên đề Phương Trình đường Tròn OXY - Luyện Thi đại Học
-
Phương Trình đường Tròn – Sách Bài Tập Toán 10 – Bài Tập Hình Học
-
Bài Tập Về Phương Trình đường Tròn
-
Sách Giải Bài Tập Toán Lớp 10 Bài 2: Phương Trình Đường Tròn
-
Phương Trình đường Tròn - Toán 10 - Thầy Nguyễn Công Chính