50 Bài Toán Về Nguyên Hàm Của Hàm Số Lượng Giác (có đáp án 2022)

Nguyên hàm của hàm số lượng giác và cách giải

A. LÝ THUYẾT

1. Một số công thức lượng giác cần nhớ

- Hệ thức lượng giác cơ bản:

sin2x+cos2x=1;1sin2x=1+cot2x;1cos2x=1+tan2x

2. Một số nguyên hàm lượng giác cơ bản

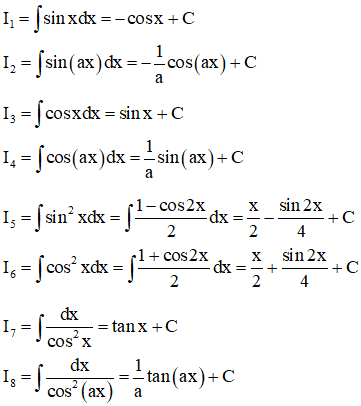
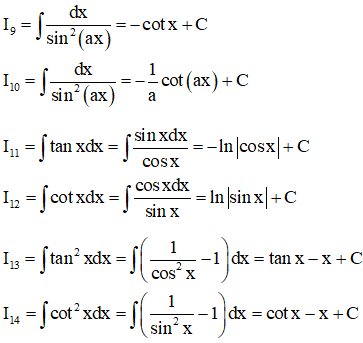
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI

1. Dạng ∫sinmx.cosnxdx trong đó m, n là các số tự nhiên

Trường hợp 1: Trong hai số m, n có ít nhất một số lẻ.

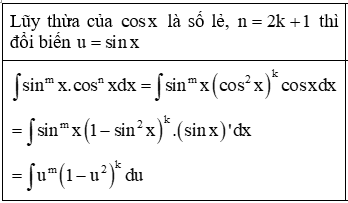
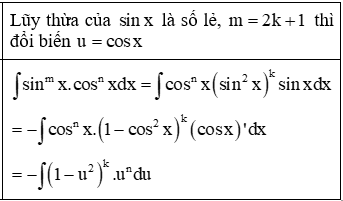
Trường hợp 2: Cả hai số m, n đều là số chẵn: Ta sử dụng công thức hạ bậc để giảm một nửa số mũ của , để làm bài toán trở nên đơn giản hơn.

2. Dạng ∫sinax.cosbxdx

∫sinax.sinbxdx; ∫cosax.cosbxdx;

∫cosax.sinbxdx.

Ta sử dụng công thức biến đổi tích thành tổng trong lượng giác.

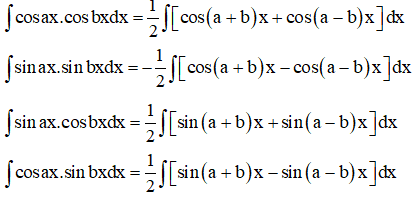
3. Dạng ∫tanmxcosnxdx trong đó m, n là các số nguyên

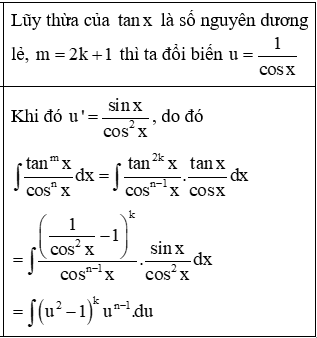
4. Đổi biến số với hàm lượng giác

Khi nguyên hàm, tích phân của các hàm số mà biểu thức của nó có chứa các dạng x2+a2,x2−a2,a2−x2, thì ta có cách biến đổi lượng giác như sau:

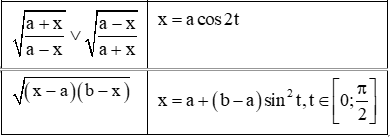
VÍ DỤ MINH HOẠ.

Ví dụ 1: Tìm I=∫sin5x.cos2xdx.

Lời giải

Vì lũy thừa của sinx là số lẻ nên ta đổi biến

u=cosx⇒du=cosx'dx

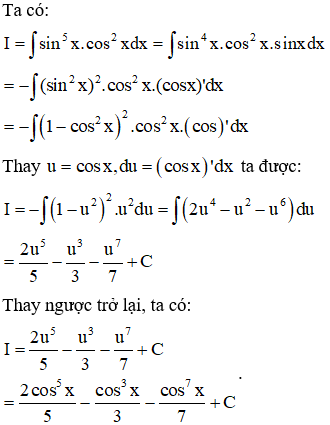
Ví dụ 2: Tìm nguyên hàm

a. A=∫tan6xcos4xdx

b. B=∫tan5xcos7xdx

Lời giải

a. Do lũy thừa của cosx là số nguyên dương chẵn nên đặt u = tanx. Từ công thức tổng quát đã chứng minh ở trên ta có:

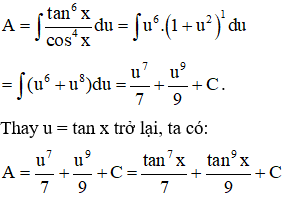
b. Do lũy thừa của là một số lẻ nên ta đặt u=1cosx, do vậy, từ công thức tổng quát chứng minh ở trên ta có

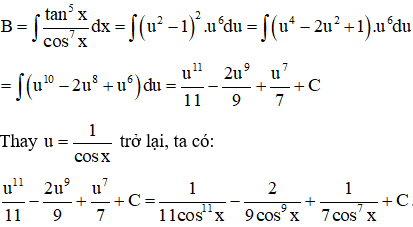
Ví dụ 3: Cho hàm số f(x) thỏa mãn f'x=x+sinxsin2x. Biết rằng f(0) = 2. Giá trị của fπ2 là:

A. fπ2=π24+23

B. fπ2=π24+83

C. fπ2=π22+23

D. fπ2=π22+83

Lời giải:

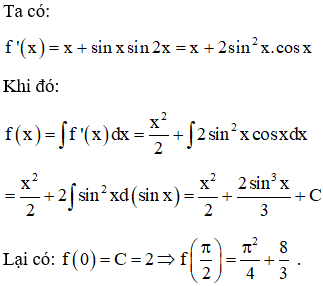
Chọn B

C. BÀI TẬP TỰ LUYỆN

Câu 1. Tìm công thức sai:

A. ∫exdx=ex+C

B. ∫axdx=axlna+C   0<a≠1

C. ∫cosxdx=sinx+C

D. ∫sinxdx=cosx+C

Câu 2. Tìm nguyên hàm của: y=sinx.sin7x   với Fπ2=0 là:

A. sin6x12+sin8x16

B. −sin6x12+sin8x16

C. sin6x12−sin8x16

D. −sin6x12+sin8x16

Câu 3. ∫1sin2x.cos2xdx bằng:

A. 2tan2x+C

B. -4cot2x+C

C. 4cot2x+C

D. 2cot2x+C

Câu 4. ∫sin2x−cos2x2dx bằng:

A. sin2x−cos2x33+C

B. −12cos2x+12sin2x2+C

C. x−12sin2x+C

D. x+14cos4x+C

Câu 5. ∫cos22x3dx bằng:

A. 32cos42x3+C

B. 12cos42x3+C

C. x2+38sin4x3+C

D. x2−43cos4x3+C

Câu 6. Hàm số F(x)=lnsinx−3cosx là một nguyên hàm của hàm số nào trong các hàm số sau đây:

A. f(x)=cosx+3sinxsinx−3cosx

B. f(x)=cosx+3sinx

C. f(x)=−cosx−3sinxsinx−3cosx

D. f(x)=sinx−3cosxcosx+3sinx

Câu 7. Tìm nguyên hàm: ∫(1+sinx)2dx

A. 23x+2cosx−14sin2x+C

B. 32x−2cosx+14sin2x+C

C. 23x−2cos2x−14sin2x+C

D. 32x−2cosx−14sin2x+C

Câu 8. Cho f(x)=4mπ+sin2x. Tìm m để nguyên hàm F(x) của f(x) thỏa mãn F(0) = 1 và Fπ4=π8

A. m=−43

B. m=−34

C. m=−34

D. m=34

Câu 9. Một nguyên hàm của hàm số y=sin3x 

A. −13cos3x 

B. −3cos3x 

C. 3cos3x 

D. 13cos3x 

Câu 10. Nguyên hàm của hàm số f(x)=tan3x là:

A. Đáp án khác

B. tan2x+1

C. tan4x4+C

D. 12tan2x+lncosx+C

Câu 11. Cặp hàm số nào sau đây có tính chất: Có một hàm số là nguyên hàm của hàm số còn lại?

A. sin2x và cos2x

B. tanx2 và 1cos2x2

C. ex và e-x

D. sin2x và sin2x

Câu 12. Một nguyên hàm của hàm số f(x)=4cos2x là:

A. 4xsin2x

B. 4tanx

C. 4+tanx

D. 4x+43tan3x

Câu 13. Họ nguyên hàm của f(x) = sin3x

A. cosx−cos3x3+C

B. −cosx+cos3x3+C

C. −cosx+1cosx+c

D. sin4x4+C

Câu 14. Nguyên hàm của hàm số fx=2sinx+cosx là:

A. 2cosx−sinx+C

B. 2cosx+sinx+C

C. −2cosx−sinx+C

D. −2cosx+sinx+C

Câu 15. Họ nguyên hàm của hàm số fx=sin2x là

A. Fx=−12cos2x+C

B. Fx=cos2x+C

C. Fx=12cos2x+C

D. Fx=-cos2x+C

Câu 16. Tính ∫cos5x.cos3xdx

A. 18sin8x+12sin2x+C

B. 12sin8x+12sin2x

C. 116sin8x+14sin2x

D. −116sin8x−14sin2x

Câu 17. ∫cos8x.sinxdx bằng:

A. 18sin8x.cosx+C

B. -18sin8x.cosx+C

C. 114cos7x−118cos9x+C

D. 118cos9x−114cos7x+C

Câu 18. ∫sin22xdx bằng:

A. 12x+18sin4x+C

B. 13sin32x+C

C. 12x−18sin4x+C

D. 12x−14sin4x+C

Câu 19. Nguyên hàm F(x) của hàm số f(x)=x+sinx thỏa mãn F(0)=19 là:

A. F(x)=−cosx+x22

B. F(x)=−cosx+x22+2

C. F(x)=cosx+x22+20

D. F(x)=−cosx+x22+20

Câu 20. Nguyên hàm F(x) của hàm số f(x)=2x+1sin2x thỏa mãn Fπ4=−1 là:

A. F(x)=−cotx+x2−π24

B. F(x)=cotx−x2+π216

C. F(x)=−cotx+x2

D. F(x)=−cotx+x2−π216

Câu 21. Cho hàm số fx=cos3x.cosx. Nguyên hàm của hàm số fx bằng 0 khi x=0 là hàm số nào trong các hàm số sau ?

A. 3sin3x+sinx

B. sin4x8+sin2x4

C. sin4x2+sin2x4

D. cos4x8+cos2x4

Câu 22. ∫3cosx2+sinxdx bằng:

A. 3ln2+sinx+C

B. −3ln2+sinx+C

C. 3sinx2+sinx2+C

D. −3sinxln2+sinx+C

Câu 23. Nguyên hàm của sinx+cosxsinx−cosx là:

A. lnsinx+cosx+C

B. 1lnsinx−cosx+C

C. lnsinx−cosx+C

D. 1sinx+cosx+C

Câu 24. ∫cotxsin2xdx bằng:

A. −cot2x2+C

B. cot2x2+C

C. −tan2x2+C

D. tan2x2+C

Câu 25. ∫sinxcos5xdx bằng:

A. −14cos4x+C

B. 14cos4x+C

C. 14sin4x+C

D. -14sin4x+C

Câu 26. ∫sin5x.cosxdx bằng:

A. sin6x6+C

B.−sin6x6+C

C. −cos6x6+C

D. cos6x6+C

Câu 27. Họ nguyên hàm của hàm số fx=e−xcosx là

A. Fx=12e−xsinx−cosx+C

B. Fx=12e−xsinx+cosx+C

C. Fx=−12e−xsinx+cosx+C

D. Fx=−12e−xsinx−cosx+C

Câu 28. Nguyên hàm của hàm số: I=∫x−2sin3xdx là:

A. F(x) = −x−2cos3x3+19sin3x+C

B. F(x) = x−2cos3x3+19sin3x+C

C. F(x) = −x+2cos3x3+19sin3x+C

D. F(x) = −x−2cos3x3+13sin3x+C

Câu 29. Biểu thức nào sau đây bằng với ∫x2sinxdx?

A. −2xcosx−∫x2cosxdx

B. −x2cosx+∫2xcosxdx

C. −x2cosx−∫2xcosxdx

D. −2xcosx+∫x2cosxdx

Câu 30. Đổi biến x = 2sint tích phân I=∫dx4−x2 trở thành

A. ∫dt

B. ∫tdt

C. ∫1tdt

D. ∫dt

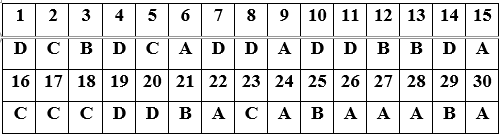
Đáp án

Xem thêm các dạng bài tập Toán lớp 12 có đáp án và lời giải chi tiết khác:

Các dạng toán về lãi suất ngân hàng và cách giải

Nguyên hàm và cách giải bài tập cơ bản

Các phương pháp tính nguyên hàm và cách giải bài tập

Nguyên hàm của hàm số phân thức hữu tỉ và cách giải

Tích phân và cách giải bài tập cơ bản