A Xm-yn 2= - Gauthmath
Math Resources/Math/ SHOW LESS195
SHOW LESS195![user avatar image]()

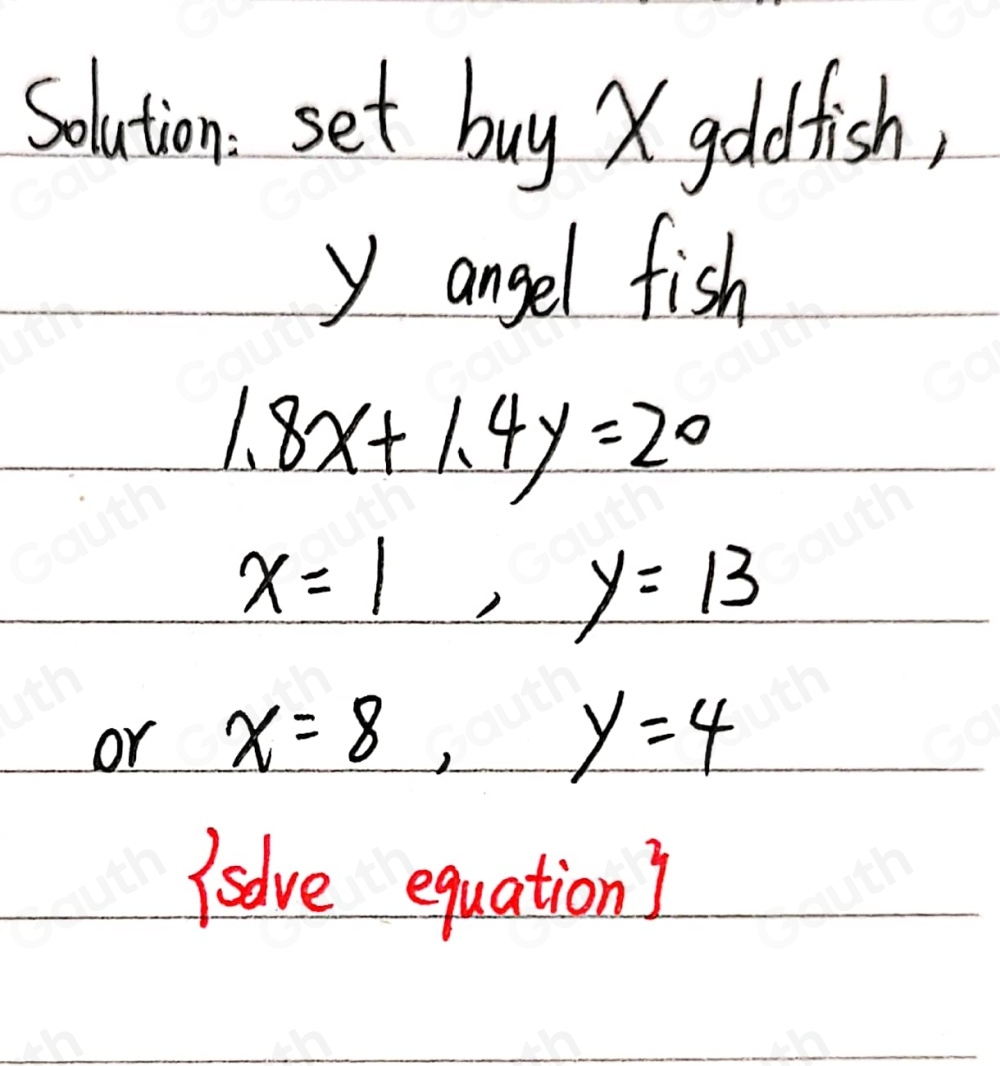 SHOW LESSClick to rate:89.9(601 votes)Search questionBy textBy image/screenshotDrop your file here orClick Hereto upload
SHOW LESSClick to rate:89.9(601 votes)Search questionBy textBy image/screenshotDrop your file here orClick Hereto upload
Question
Solution
Từ khóa » (xm-yn)2
-
Solve Simplificationorothersimpleresults (xm-yn)2 Tiger Algebra Solver
-
(xm-yn)² Por Favor Me Ayudan - t
-
If X^my^n = (x + Y)^m + N . Prove That D^2ydx^2 = 0 . - Toppr
-
[Solved] If Xm Yn = 2(x + Y)m + N , Find The Val
-
( Xm -yn )2 | Descubre Cómo Resolverlo En QANDA
-
1-D Signal I(xm ,yn ,kp ) From A Pixel (xm ,yn ) Close To The...
-
If Xmyn=x+ym+n, Then The Value Of Dydx Is - BYJU'S
-
If X^(m) Y^(n) =2(x+y)^(m+n), The Value Of (dy)/(dx) Is - Doubtnut
-
If Xm . Yn = (x + Y)m+n, Then Show That Dydxdydx=yx
-
If Xm Yn = (x + Y)m + N, Prove That From Class 12 CBSE ... - Zigya
-
Is X/m(m^2 + N^2 + K^2) = Xm + Yn + Zk? (1) Z/k = X/m (2) - GMAT Club
-
If Xm Yn =(x+y)m+n , Then (dy/dx) Is: - Tardigrade
-
If Xm Yn =(x+y)m+n , Then (dy/dx) Is - Tardigrade App