B. Giới Hạn Của Hàm Số. Hàm Số Liên Tục - Tìm đáp án, Giải Bài Tập, để

1. Trang chủ
2. Lớp 11
3. Toán học
4. Toán Nâng Cao
5. ĐẠI SỐ VÀ GIẢI TÍCH 11 NÂNG CAO
6. B. Giới hạn của hàm số. Hàm số liên tục

B. Giới hạn của hàm số. Hàm số liên tục

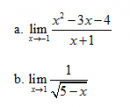
Câu 21 trang 151 SGK Đại số và Giải tích 11 Nâng cao

Áp dụng định nghĩa giới hạn Xem lời giải

Câu 22 trang 151 SGK Đại số và Giải tích 11 Nâng cao

Cho hàm số Xem lời giải

Câu 23 trang 152 SGK Đại số và Giải tích 11 Nâng cao

Tìm các giới hạn sau : Xem lời giải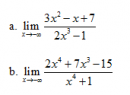

Câu 24 trang 152 SGK Đại số và Giải tích 11 Nâng cao

Tìm các giới hạn sau : Xem lời giải

Câu 25 trang 152 SGK Đại số và Giải tích 11 Nâng cao

Tìm các giới hạn sau : Xem lời giải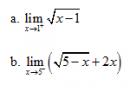

Câu 26 trang 158 SGK Đại số và Giải tích 11 Nâng cao

Áp dụng định nghĩa giới hạn Xem lời giải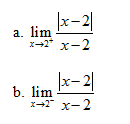

Câu 27 trang 158 SGK Đại số và Giải tích 11 Nâng cao

Tìm các giới hạn sau (nếu có) : Xem lời giải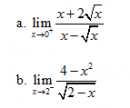

Câu 28 trang 158 SGK Đại số và Giải tích 11 Nâng cao

Tìm các giới hạn sau : Xem lời giải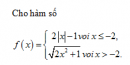

Câu 29 trang 159 SGK Đại số và Giải tích 11 Nâng cao

Cho hàm số Xem lời giải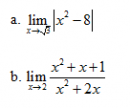

Câu 30 trang 159 SGK Đại số và Giải tích 11 Nâng cao

Tìm các giới hạn sau : Xem lời giải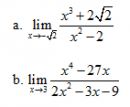

Câu 31 trang 159 SGK Đại số và Giải tích 11 Nâng cao

Tìm các giới hạn sau : Xem lời giải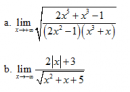

Câu 32 trang 159 SGK Đại số và Giải tích 11 Nâng cao

Tìm các giới hạn sau : Xem lời giải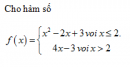

Câu 33 trang 159 SGK Đại số và Giải tích 11 Nâng cao

Cho hàm số Xem lời giải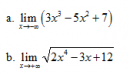

Câu 34 trang 163 SGK Đại số và Giải tích 11 Nâng cao

Tìm các giới hạn sau : Xem lời giải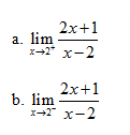

Câu 35 trang 163 SGK Đại số và Giải tích 11 Nâng cao

Tìm các giới hạn sau : Xem lời giải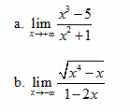

Câu 36 trang 163 SGK Đại số và Giải tích 11 Nâng cao

Tìm các giới hạn sau : Xem lời giải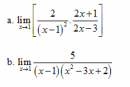

Câu 37 trang 163 SGK Đại số và Giải tích 11 Nâng cao

Tính Xem lời giải

Câu 38 trang 166 SGK Đại số và Giải tích 11 Nâng cao

Tìm các giới hạn sau : Xem lời giải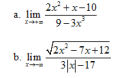

Câu 39 trang 166 SGK Đại số và Giải tích 11 Nâng cao

Tìm các giới hạn sau : Xem lời giải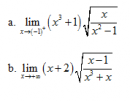

Câu 40 trang 166 SGK Đại số và Giải tích 11 Nâng cao

Tìm các giới hạn sau : Xem lời giải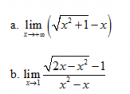

Câu 41 trang 166 SGK Đại số và Giải tích 11 Nâng cao

Tìm các giới hạn sau : Xem lời giải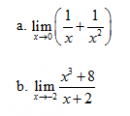

Câu 42 trang 167 SGK Đại số và Giải tích 11 Nâng cao

Tìm các giới hạn sau : Xem lời giải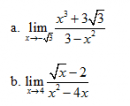

Câu 43 trang 167 SGK Đại số và Giải tích 11 Nâng cao

Tìm các giới hạn sau : Xem lời giải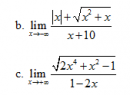

Câu 44 trang 167 SGK Đại số và Giải tích 11 Nâng cao

Tìm các giới hạn sau : Xem lời giải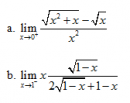

Câu 45 trang 167 SGK Đại số và Giải tích 11 Nâng cao

Tìm các giới hạn sau : Xem lời giải

Bài học tiếp theo

Câu hỏi và bài tập ôn tập chương IV Bài tập trắc nghiệm khách quan - Chương IV. Giới hạn - Toán 11 Nâng cao Bài 1. Khái niệm đạo hàm Bài 2. Các quy tắc tính đạo hàm Bài 3. Đạo hàm của các hàm số lượng giác Bài 4. Vi phân Bài 5. Đạo hàm cấp cao Câu hỏi và bài tập ôn tập chương V Bài tập trắc nghiệm khách quan - Chương V. Đạo hàm - Toán 11 Nâng cao ÔN TẬP CUỐI NĂM ĐẠI SỐ VÀ GIẢI TÍCH - TOÁN 11 NÂNG CAO

Bài học bổ sung

Bài học liên quan

Bài 1. Các hàm số lượng giác Bài 2. Phương trình lượng giác cơ bản Bài 3. Một số dạng phương trình lượng giác đơn giản Câu hỏi và bài tập ôn tập chương I Bài tập trắc nghiệm khách quan - Chương I. Hàm số lượng giác và phương trình lượng giác - Toán 11 Nâng cao A. Tổ hợp B. Xác suất Câu hỏi và bài tập ôn tập chương II Bài tập trắc nghiệm khách quan - Chương II. Tổ hợp và xác suất - Toán 11 Nâng cao Bài 1. Phương pháp quy nạp toán học Bài 2. Dãy số Bài 3. Cấp số cộng Bài 4. Cấp số nhân Câu hỏi và bài tập ôn tập chương III Bài tập trắc nghiệm khách quan - Chương III. Dãy số. Cấp số cộng và cấp số nhân - Toán 11 Nâng cao A. Giới hạn của dãy số B. Giới hạn của hàm số. Hàm số liên tục Câu hỏi và bài tập ôn tập chương IV Bài tập trắc nghiệm khách quan - Chương IV. Giới hạn - Toán 11 Nâng cao Bài 1. Khái niệm đạo hàm Bài 2. Các quy tắc tính đạo hàm Bài 3. Đạo hàm của các hàm số lượng giác Bài 4. Vi phân Bài 5. Đạo hàm cấp cao Câu hỏi và bài tập ôn tập chương V Bài tập trắc nghiệm khách quan - Chương V. Đạo hàm - Toán 11 Nâng cao ÔN TẬP CUỐI NĂM ĐẠI SỐ VÀ GIẢI TÍCH - TOÁN 11 NÂNG CAO

Từ khóa phổ biến

Hỏi bài