Bài 1.1, 1.2, 1.3, 1.4, 1.5 Phần Bài Tập Bổ Sung Trang 115, 116 SBT ...

Bài I.1

Cho hình bs 10 (hai đường thẳng \(a, b\) song song với nhau và hai đường thẳng c, d song song với nhau; Dm, Cp, Bq và An tương ứng là các tia phân giác).

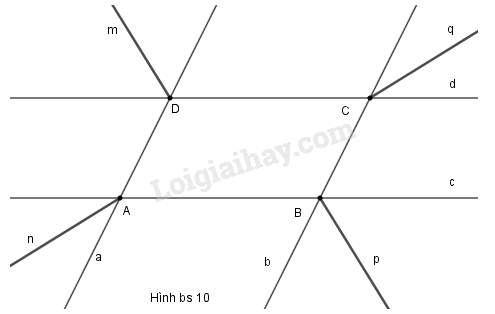
a) Chứng minh: An // Cp và Dm // Bq.

b) Chứng minh: An vuông góc với Bq.  

Phương pháp giải:

Sử dụng dấu hiệu nhận biết hai đường thẳng song song 

Một đường thẳng cắt hai đường thẳng phân biệt tạo thành cặp góc so le trong bằng nhau (cặp góc đồng vị bằng nhau) thì hai đường thẳng đó song song với nhau

Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau

Lời giải chi tiết:

 

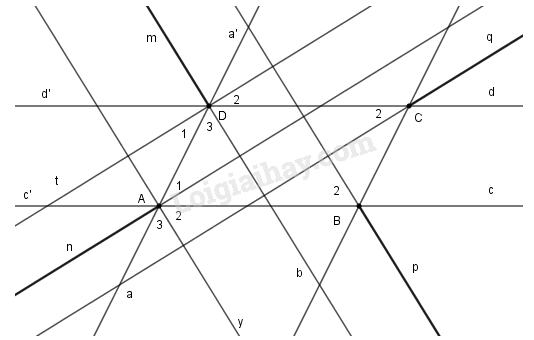
Kẻ thêm các tia đối của tia An, Cq, Bp, Dm và đặt tên như hình vẽ.

Khi đó vì An, Cq, Bp, Dm là các tia phân giác góc A, C, B, D nên ta cũng có các tia đối tương ứng là phân giác của các góc DAB, DCB, ABC, ADC.

Kẻ thêm đường thẳng qua D là phân giác của góc d’DA và đường thẳng qua A là phân giác của góc aAB.

+) Vì \(d//c\)  nên \(\widehat {d'DA} = \widehat {DAB}\) (hai góc so le trong). Mà \(\widehat {{D_1}} = \dfrac{1}{2}\widehat {d'DA},\widehat {{A_1}} = \dfrac{1}{2}\widehat {DAB}\) (tính chất tia phân giác)

Suy ra \(\widehat {{D_1}} = \widehat {{A_1}}\) mà hai góc ở vị trí so le trong nên \(Dt//An\)  (1)

Vì \(a//b\)  nên \(\widehat {a'DC} = \widehat {DCB}\) (hai góc so le trong). Mà \(\widehat {{D_2}} = \dfrac{1}{2}\widehat {a'DC},\widehat {{C_2}} = \dfrac{1}{2}\widehat {DCB}\) (tính chất tia phân giác)

Suy ra \(\widehat {{D_2}} = \widehat {{C_2}}\) mà hai góc ở vị trí so le trong nên \(Dt//Cq\)  (2)

Từ (1) và (2) suy ra \(An//Cq\)

+) Vì \(d//c\)  nên \(\widehat {aAB} = \widehat {ADC}\) (hai góc đồng vị). Mà \(\widehat {{A_3}} = \dfrac{1}{2}\widehat {aAB},\widehat {{D_3}} = \dfrac{1}{2}\widehat {ADC}\) (tính chất tia phân giác)

Suy ra \(\widehat {{D_3}} = \widehat {{A_3}}\) mà hai góc ở vị trí đồng vị nên \(Dm//Ay\)  (3)

Vì \(a//b\)  nên \(\widehat {aAB} = \widehat {ABC}\) (hai góc so le trong). Mà \(\widehat {{A_2}} = \dfrac{1}{2}\widehat {aAB},\widehat {{B_2}} = \dfrac{1}{2}\widehat {ABC}\) (tính chất tia phân giác)

Suy ra \(\widehat {{B_2}} = \widehat {{A_2}}\) mà hai góc ở vị trí so le trong nên \(Bq//Ay\)  (4)

Từ (3) và (4) suy ra \(Dm//Bq\) 

b) Ta có \(\widehat {{D_1}} = \dfrac{1}{2}\widehat {d'Da},\widehat {{D_3}} = \dfrac{1}{2}\widehat {ADC}\)  (tính chất tia phân giác)

Mà \(\widehat {d'DA} + \widehat {ADC} = {180^0}\) (hai góc kề bù)

Nên \(\widehat {{D_1}} + \widehat {{D_3}}\) \( = \dfrac{1}{2}\left( {\widehat {d'DA} + \widehat {ADC}} \right)\) \( = \dfrac{1}{2}{.180^0} = {90^0}\)

Suy ra \(Dt \bot Dm\) mà \(An//Dt\) và \(Dm//Bq\) nên \(An \bot Bq\).