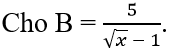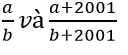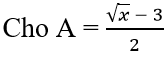Bài I.1 Trang 115 Sách Bài Tập Toán 7 Tập 1 Cho Hình Bs 10(hai ...

Học liệu Hỏi đáp Đăng nhập Đăng ký

• Học bài
• Hỏi bài
• Kiểm tra
• ĐGNL
• Thi đấu
• Thư viện số
• Bài viết Cuộc thi Tin tức Blog học tập
• Trợ giúp
• Về OLM

OLM App phiên bản mới, cập nhật trải nghiệm ngay!

🔥ĐẤU TRƯỜNG TRỞ LẠI, THỬ THÁCH TĂNG CẤP!!! THAM GIA NGAY

Chính thức mở đề thi thử tốt nghiệp THPT trên máy tính từ 27/12/2025, xem ngay.

OLM Class tuyển sinh lớp bứt phá học kỳ II! Đăng ký ngay

• Mẫu giáo
• Lớp 1
• Lớp 2
• Lớp 3
• Lớp 4
• Lớp 5
• Lớp 6
• Lớp 7
• Lớp 8
• Lớp 9
• Lớp 10
• Lớp 11
• Lớp 12
• ĐH - CĐ

K Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xác nhận câu hỏi phù hợp

×

Chọn môn học Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên Mua vip

• Tất cả
• Mới nhất
• Câu hỏi hay
• Chưa trả lời
• Câu hỏi vip

PT phạm thị khánh ly 9 tháng 10 2019 - olm

Bài I.1 trang 115 sách bài tập Toán 7 Tập 1

 Cho hình bs 10(hai đường thẳng a, b song song với nhau và hai đường thẳng c, d song song với nhau; Dm, Cp, Bq và An tương ứng là các tia phân giác).

a) Chứng minh: An // Cp và Dm // Bq.

b) Chứng minh: An vuông góc với Bq.

#Hỏi cộng đồng OLM #Toán lớp 7 2 M •Mυη• 9 tháng 10 2019

TL : 

a) Vẽ thêm các tia đối của các tia Dm, Cp, Bq và An.

Vẽ thêm các đường phân giác Ds và Ar của góc ∠D và ∠A.

Khi đó chứng minh được Cp song song với Ds.

Tương tự chứng minh được Ar song song với Dm.

Từ đó suy ra được: An // Cp và Dm // Bq.

b) Sử dụng tính chất tia phân giác của hai góc bù nhau có được Ds, Dm vuông góc với nhau.

Từ đó suy ra được: An vuông góc với Bq.

Hok tốt

Đúng(0) TH THE HACK 9 tháng 10 2019

Giỏi thế

Đúng(0) Xem thêm câu trả lời Các câu hỏi dưới đây có thể giống với câu hỏi trên CT Chàng Trai 2_k_7 23 tháng 10 2019 - olm

Cho hình bs 10(hai đường thẳng a, b song song với nhau và hai đường thẳng c, d song song với nhau; Dm, Cp, Bq và An tương ứng là các tia phân giác).

a) Chứng minh: An // Cp và Dm // Bq.

b) Chứng minh: An vuông góc với Bq.

#Hỏi cộng đồng OLM #Toán lớp 7 0 TT Teen titans go 5a 13 tháng 5 2019 - olm

 Cho tam giác ABC. Từ điểm D trên cạnh BC, kẻ các đường b thẳng song song với các cạnh AB và AC, chúng cắt các cạnh AC và AB theo thứ tự tại F và E.

Chứng minh rằng: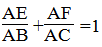 

#Hỏi cộng đồng OLM #Toán lớp 7 5 TT Teen titans go 5a 13 tháng 5 2019

TOÁN LỚP 8 NHA

Đúng(0) NV Nguyễn Viết Ngọc 13 tháng 5 2019

chứng minh rằng cái j hả bn

Đúng(0) Xem thêm câu trả lời VN Vũ Nga 31 tháng 8 2020 - olm                                      Cho hình bs 7 ( đường thẳng a song song với đường thẳng b và đường thẳng c song song với đường thẳng d).Cho biết số đo của các góc \(\widehat{C_1}\),\(^{\widehat{D}_2}\) và giải thích cách tìm ra kết quả.Ai cho mình kết quả sớm nhất mình sẽ tích...Đọc tiếp

                                     

Cho hình bs 7 ( đường thẳng a song song với đường thẳng b và đường thẳng c song song với đường thẳng d).Cho biết số đo của các góc \(\widehat{C_1}\),\(^{\widehat{D}_2}\) và giải thích cách tìm ra kết quả.

Ai cho mình kết quả sớm nhất mình sẽ tích cho

 

#Hỏi cộng đồng OLM #Toán lớp 7 4 VN Vũ Nga 31 tháng 8 2020

         Hình bs 7

Đúng(0) HC Hoa Cửu 31 tháng 8 2020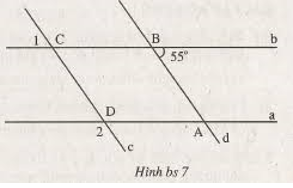

                                                     Bài giải

a b c d

Bạn ơi hình bs là gì ? Mà lấy đâu ra \(\widehat{C_1}\text{ ; }\widehat{D_2}\)

Đúng(0) Xem thêm câu trả lời LD Lân Dũng 1 tháng 11 2018 - olm

Bài 1

Tìm x ∈ Z để B có giá trị nguyên.

#Hỏi cộng đồng OLM #Toán lớp 7 1 T ✨🔱TMT_VN🔱✨ 1 tháng 11 2018

vì tập hợp  N là số nguyên

mà N \(\in\)Z

=> x=N

Đúng(0) L lemailinh 9 tháng 9 2018 - olm

Cho a, b ∉ Z, b > 0. So sánh 2 số hữu tỉ

 

#Hỏi cộng đồng OLM #Toán lớp 7 0 LD Lân Dũng 1 tháng 11 2018 - olm

Bài 1: 

Tìm x ∈ Z và x < 30 để A có giá trị nguyên

#Hỏi cộng đồng OLM #Toán lớp 7 1 T ✨🔱TMT_VN🔱✨ 1 tháng 11 2018

tập hợp N là số nguyên    (1)

mà A  = giá tri nguyên      (2)

và x < 30                          (3)

từ (1),(2),(3) ta  có:

x={0;1;2;3;...;29}

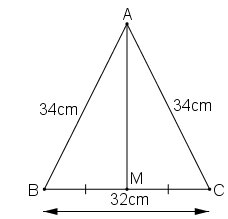
Đúng(0) AT Ánh trang 1 tháng 5 2019 - olm

Tam giác ABC cân tại A có AB = CD = 34cm, BC = 32cm. Kẻ đường trung tuyến AM.

a. Chứng minh rằng AM ⊥ BC.

b. Tính độ dài AM

mk vẽ hình rồi nha chỉ cần các bạn giải là được

#Hỏi cộng đồng OLM #Toán lớp 7 1 NT Nguyễn Thị Linh Giang 1 tháng 5 2019

a. Xét ΔAMB và ΔAMC, ta có:

AM = AC (gt)

BM = CM (gt)

AM cạnh chung

Suy ra: ΔAMB = ΔAMC (c.c.c)

Suy ra: ∠(AMB) = ∠(AMC) (1)

Lại có: ∠(AMB) + ∠(AMC) = 180o (hai góc kề bù) (2)

Từ (1) và (2) suy ra: ∠(AMB) = ∠(AMC) = 90o

Vậy AM ⊥ BC.

b. Tam giác AMB có ∠(AMB) = 90o

Áp dụng định lí Pi-ta-go vào tam giác vuông AMB, ta có:

AB2 = AM2 + BM2 ⇒ AM2 = AB2 - BM2 = 342 - 162

= 1156 - 256 = 900

Suy ra: AM = 30 (cm).

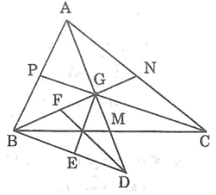
Đúng(0) TT Teen titans go 5a 1 tháng 5 2019 - olm Gọi G là trọng tâm của tam giác ABC. Vẽ điểm D sao cho G là trung điểm của AD. Chứng minh rằng:a. Các cạnh của tam giác BGD bằng 2/3 các đường trung tuyến của tam giác ABC.b. Các đường trung tuyến của tam giá BGD bằng một nửa các cạnh của tam giác...Đọc tiếp

Gọi G là trọng tâm của tam giác ABC. Vẽ điểm D sao cho G là trung điểm của AD. Chứng minh rằng:

a. Các cạnh của tam giác BGD bằng 2/3 các đường trung tuyến của tam giác ABC.

b. Các đường trung tuyến của tam giá BGD bằng một nửa các cạnh của tam giác ABC.

 

#Hỏi cộng đồng OLM #Toán lớp 7 2 NT Nguyễn Thị Linh Giang 1 tháng 5 2019

a. Gọi AM, BN, CP lần lượt là các đường trung tuyến của ΔABC. Các đường trung tuyến cắt nhau tại G.

Ta có: AG = GD (gt)

AG = 2GM (tính chất đường trung tuyến)

Suy ra: GD = 2GM

Mà GD = GM + MD ⇒ GM = MD

Xét ΔBMD và ΔCMG, ta có:

BM = CM (gt)

∠(BMD) = ∠(CMG) (đối đỉnh)

MD = GM (chứng minh trên)

Suy ra: ΔBMD = ΔCMG (c.g.c)

⇒ BD = CG (hai cạnh tương ứng)

Mặt khác: CG = 2/3 CP (tính chất đường trung tuyến)

Suy ra: BD = 2/3 CP (1)

Lại có: BG = 2/3 BN (tính chất đường trung tuyến) (2)

Và AG = 2/3 AM (tính chất đường trung tuyến)

Suy ra: GD = 2/3 AM (3)

Từ (1), (2) và (3) suy ra các cạnh của tam giác BGD bằng 2/3 các đường trung tuyến của tam giác ABC.

b. Ta có: GM = MD (chứng minh trên)

Suy ra BM là đường trung tuyến của tam giác BGD.

Suy ra: BM = 1/2 BC (4)

Kẻ đường trung tuyến GE và DF của tam giác BGD, ta có:

FG = 1/2 BG (tính chất đường trung tuyến)

GN = 1/2 GB (tính chất đường trung tuyến)

Suy ra: FG = GN

Xét ΔDFG và ΔANG, ta có:

AG = GD (gt)

∠(DGF) = ∠(AGN) (đối đỉnh)

GF = GN (chứng minh trên)

Suy ra: ΔDFG = ΔANG (c.g.c) ⇒ DF = AN

Mà AN = 1/2 AC (gt)

Suy ra: DF = 1/2 AC (5)

Mặt khác: BD = CG (chứng minh trên)

ED = 1/2 BD (vì E là trung điểm BD)

GP = 1/2 CG (tính chất đường trung tuyến)

Suy ra: ED = GP

Lại có: ΔBMD = ΔCMG (chứng minh trên)

⇒ ∠(BDM) = ∠(CGM) hay ∠(EDG) = ∠(CGM)

(CGM) = (PGA) (đối đỉnh)

Suy ra: ∠(EDG) = ∠(PGA)

AG = GD (gt)

Suy ra: ΔPGA = ΔEDG (c.g.c) ⇒ GE = AP mà AP = 1/2 AB (gt)

Do đó: GE = 1/2 AB(6)

Từ (4), (5) và (6) suy ra các đường trung tuyến của ΔBGD bằng một nửa cạnh của ΔABC.

Đúng(0) TT Teen titans go 5a 1 tháng 5 2019

ko cần vẽ hình đâu nhé giải thôi

Đúng(0) Xem thêm câu trả lời S Setsuko 6 tháng 10 2017 - olm

Cho hình bs 10 (hai đường thẳng a, b song song với nhau và hai đường thẳng c, d song song với nhau; Dm, Cp, Bq và An tương ứng là các tia phân giác)

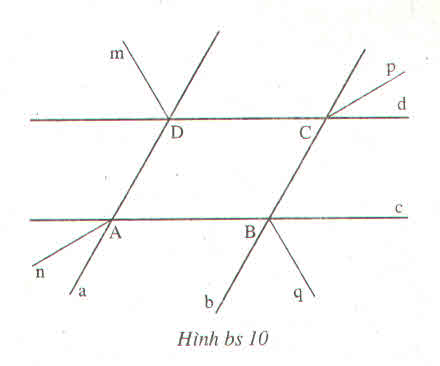
a) Chứng minh : An // Cp và Dm //Bq

b) Chứng minh : An vuông góc với Bq

#Hỏi cộng đồng OLM #Toán lớp 7 0 Xếp hạng Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên

• Tuần
• Tháng
• Năm

• B 🐊Bombardiro💣Crocodilo✈️ 7 GP
• HG Happy great day GD ! 6 GP
• E ✦ ꧁𝓑é✿𝓬𝓱í𝓹꧂ ✦ 6 GP
• DM ༒☬Đăng Minh☬༒ (Meokonhonguongthuoc) 6 GP
• NB Nguyễn Bá Tĩnh 4 GP
• NT Nguyễn Thanh Trúc 4 GP
• NT Nguyễn Trường An 4 GP
• NT Nguyễn Thị Bảo Linh 4 GP
• NT Nguyễn Trường Tiến 4 GP
• O ꧁༺©ⓤ✞ঔৣ㊎۝ɦƯղɕლɑꜱζℰℜɦỒղղɦ¡Êղ2ƙ13✿❤☯... VIP 4 GP

Học liệu Hỏi đáp Link rút gọn Link rút gọn Để sau Đăng ký

Các khóa học có thể bạn quan tâm

× Mua khóa học Tổng thanh toán: 0đ (Tiết kiệm: 0đ) Tới giỏ hàng Đóng ×

Yêu cầu VIP

×

Học liệu này đang bị hạn chế, chỉ dành cho tài khoản VIP cá nhân, vui lòng nhấn vào đây để nâng cấp tài khoản.