Bài 1.11 Trang 15 Sách Bài Tập Giải Tích 12: Tìm Cực Trị Của Các Hàm ...

Tìm cực trị của các hàm số sau:

a) \(y =  - 2{x^2} + 7x - 5\)                                                   

b) \(y = {x^3} - 3{x^2} - 24x + 7\)

c) \(y = {x^4} - 5{x^2} + 4\)                                                     

d) \(y = {(x + 1)^3}(5 - x)\)

e) \(y = {(x + 2)^2}{(x - 3)^3}\)

Hướng dẫn làm bài:

a)  \(y =  - 2{x^2} + 7x - 5\)   . TXĐ: R

\(\eqalign{ & y’ = - 4x + 7,y’ = 0 < = > x = {7 \over 4} \cr & y” = - 4 = > y”({7 \over 4}) = - 4 < 0 \cr} \)    

Vậy \(x = {7 \over 4}\) là điểm cực đại của hàm số và \({y_{CD}} = {9 \over 8}\)

b) \(y = {x^3} - 3{x^2} - 24x + 7\) . TXĐ: R

\(y’ = 3{x^2} - 6x - 24 = 3({x^2} - 2x - 8)\)

\(y’ = 0 \Leftrightarrow \left[ \matrix{ x = - 2 \hfill \cr x = 4 \hfill \cr} \right.\)

Vì \(y”( - 2) =  - 18 < 0,y”(4) = 18 > 0\) nên hàm số đạt cực đại tại x = - 2 ; đạt cực tiểu tại x = 4 và   yCĐ = y(-2) = 35 ; yCT = y(4) = -73.

c) \(y = {x^4} - 5{x^2} + 4\) 

 TXĐ:  R

\(\eqalign{ & = {{2{x^2} - 2{m^2} - {x^2} - 2mx + 3} \over {{{(x - m)}^2}}} = {{{x^2} - 2mx - 2{m^2} + 3} \over {{{(x - m)}^2}}} \cr & y’ = 4{x^3} - 10x = 2x(2{x^2} - 5) \cr} \)

Advertisements (Quảng cáo)

$$y’ = 0 \Leftrightarrow \left[ \matrix{ x = 0 \hfill \cr x = - \sqrt {{5 \over 2}} \hfill \cr x = \sqrt {{5 \over 2}} \hfill \cr} \right.$$

Vì \(y”( \pm \sqrt {{5 \over 2}} ) = 20 > 0,y”(0) =  - 10 < 0\)

Nên hàm số đạt cực đại tại x = 0, đạt cực tiểu tại \(x =  \pm \sqrt {{5 \over 2}} \) và ta có:

                             yCĐ = y(0)  = 4 , \({y_{_{CT}}} = y( \pm \sqrt {{5 \over 2}} ) =  - {9 \over 4}\)

d)  TXĐ:  R

\(y’ =  - {(x + 1)^3} + 3{(x + 1)^2}(5 - x) = 2{(x + 1)^2}(7 - 2x)\)

\(y’ = 0 \Leftrightarrow \left[ \matrix{ x = - 1 \hfill \cr x = {7 \over 2} \hfill \cr} \right.\)

Bảng biến thiên:

 

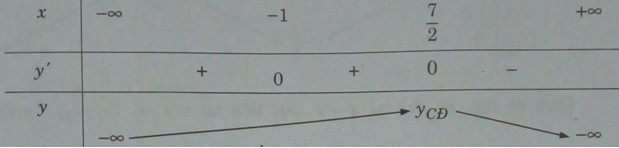
Hàm số đạt cực đại tại \(x = {7 \over 2};{y_{CD}} = y({7 \over 2}) = {{2187} \over {16}}\)

e)  TXĐ: R

\(y’ = 2(x + 2){(x - 3)^3} + 3{(x + 2)^2}{(x - 3)^2} = 5x(x + 2){(x - 3)^2}\)

\(y’ = 0 \Leftrightarrow \left[ \matrix{ x = - 2 \hfill \cr x = 0 \hfill \cr x = 3 \hfill \cr} \right.\) 

Bảng biến thiên:

 

Từ đó suy ra yCĐ = y(-2) = 0 ; yCT = y(0) = -108.