Bài 1. Số Phức - Củng Cố Kiến Thức
Có thể bạn quan tâm
Bài học này cho ta biết tập hợp số phức, một tập hợp chứa tập hợp số thực, với các quy tắc tính toán tương tự, trong đó mọi số thực âm đều có căn bậc hai, mọi phương trình bậc hai đều có nghiệm.
1. Số i
${i^2} = - 1$Lý do ${i^2} = - 1$ là vì: 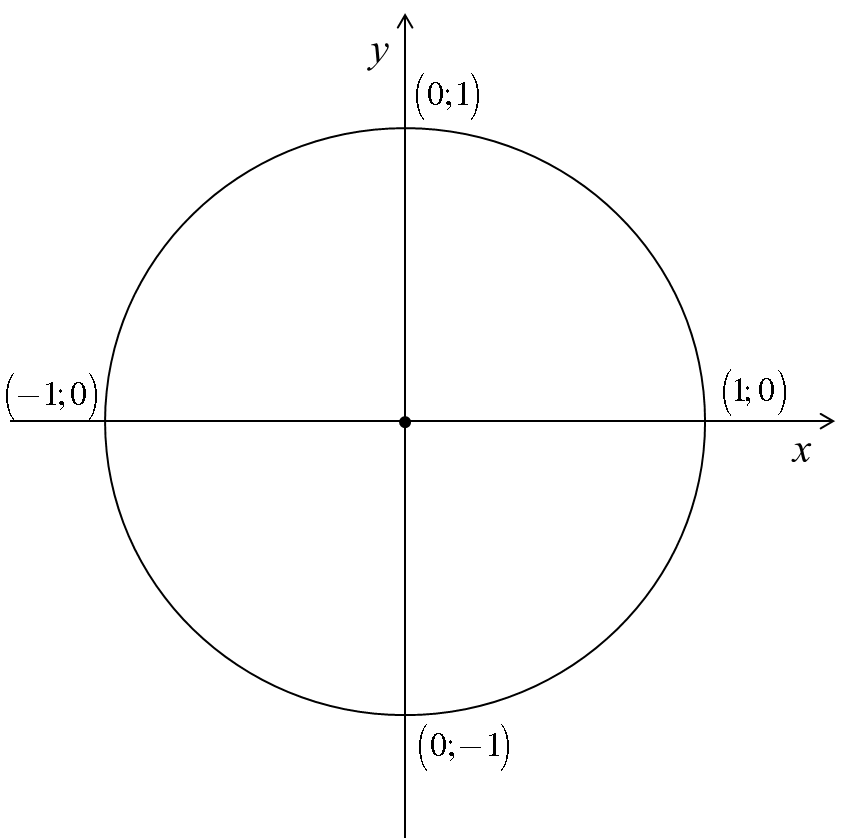 Cho vectơ $(1;0)$, tức số 1 trên trục hoành, quay một góc $90^o$ bằng toán tử $i$, ta viết $i1$, và thu được vectơ $(0;1)$, chính là số 1 trên trục tung. Giả sử cho toán tử $i$ tác dụng hai lần lên số 1, tức $({i^2})1,$ bằng cách quay vectơ $(1;0),$ góc $90^o$ theo 2 lần, chúng ta thu được vectơ $(-1;0),$ tức số $-1$ trên trục hoành. Vì vậy ${i^2} = - 1.$
Cho vectơ $(1;0)$, tức số 1 trên trục hoành, quay một góc $90^o$ bằng toán tử $i$, ta viết $i1$, và thu được vectơ $(0;1)$, chính là số 1 trên trục tung. Giả sử cho toán tử $i$ tác dụng hai lần lên số 1, tức $({i^2})1,$ bằng cách quay vectơ $(1;0),$ góc $90^o$ theo 2 lần, chúng ta thu được vectơ $(-1;0),$ tức số $-1$ trên trục hoành. Vì vậy ${i^2} = - 1.$
2. Định nghĩa số phức
Mỗi biểu thức dạng a + bi, trong đó ${i^2} = - 1$ được gọi là một số phức.
Đối với số phức z = a + bi, ta nói a là phần thực, b là phần ảo của z.
3. Số phức bằng nhau
Hai số phức là bằng nhau nếu phần thực và phần ảo của chúng tương ứng bằng nhau:
$a + bi = c + di \Leftrightarrow a = c,b = d$
4. Biểu diễn hình học số phức
Điểm $M\left( {a;b} \right)$ trong một hệ tọa độ vuông góc của mặt phẳng được gọi là điểm biểu diễn số phức z = a + bi.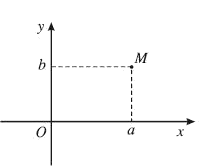
5. Môđun của số phức
Giả sử số phức $z = a + bi$ được biểu diễn bởi điểm $M\left( {a;b} \right)$ trên mặt phẳng tọa độ như hình bên dưới. 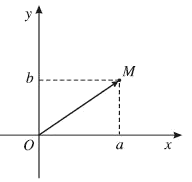 Độ dài của vectơ $\overrightarrow {OM} $ được gọi là môđun của số phức z và kí hiệu là $\left| z \right|$. $\left| z \right| = \left| {\overrightarrow {OM} } \right|$ hay $\left| a + bi \right| = \left| {\overrightarrow {OM} } \right|$$\left| {a + bi} \right| = \sqrt {{a^2} + {b^2}} $Ví dụ: $\left| {1 + i\sqrt 3 } \right| = \sqrt {1 + {{\left( {\sqrt 3 } \right)}^2}} = 2.$
Độ dài của vectơ $\overrightarrow {OM} $ được gọi là môđun của số phức z và kí hiệu là $\left| z \right|$. $\left| z \right| = \left| {\overrightarrow {OM} } \right|$ hay $\left| a + bi \right| = \left| {\overrightarrow {OM} } \right|$$\left| {a + bi} \right| = \sqrt {{a^2} + {b^2}} $Ví dụ: $\left| {1 + i\sqrt 3 } \right| = \sqrt {1 + {{\left( {\sqrt 3 } \right)}^2}} = 2.$
6. Số phức liên hợp
Cho số phức z = a + bi. Ta gọi a-bi là số phức liên hợp củaz và kí hiệu là $\overline z = a - bi$.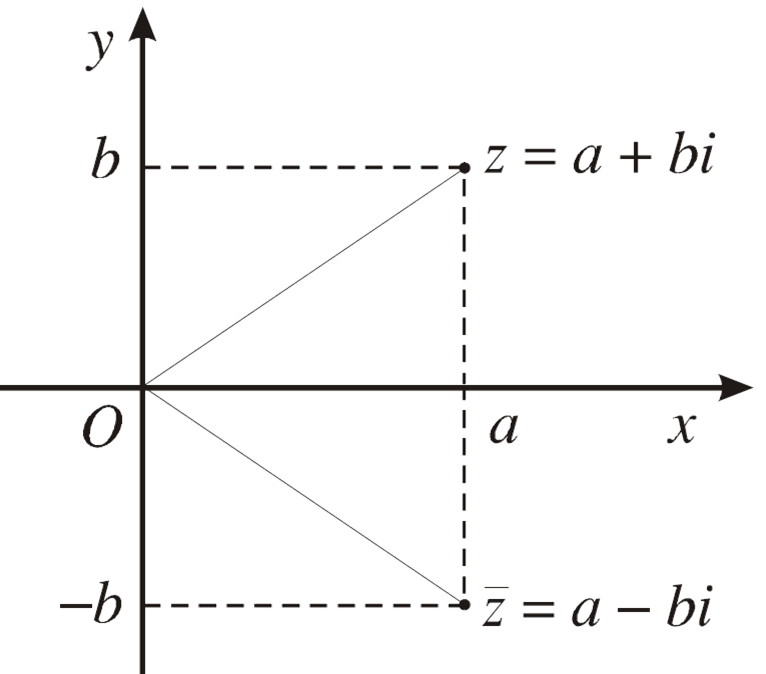
Từ khóa » Trục Thực Trục ảo
-
Số Phức Là Gì? Giải Thích Dễ Hiểu Về Số Phức - Minh Nguyen
-
Số Phức – Wikipedia Tiếng Việt
-
Số Phức Và Các Khái Niệm Cơ Bản - Toán Thầy Định
-
Tổng Hợp Lý Thuyết Toán 12 Chương Số Phức Chọn Lọc - Kiến Guru
-
[ Định Nghĩa SỐ PHỨC ] Là Gì ? Một Số Tổng Quan Và Khái Niệm.
-
Định Nghĩa Và Phép Toán Về Số Phức - Baitap123
-
Các Dạng Toán Tìm Phần Thực Và Phần Ảo Của Số Phức - Marathon
-
Số Phức Là Gì, ý Nghĩa Và Khái Niệm Số Phức Cùng Ví Dụ Minh Họa
-
Số Phức đối Là Gì, Số Phức đối Của Z Là Gì, Cách Biểu Diễn
-
Sự Biểu Diễn Của Số Phức - Tỷ Mỷ Làm Toán. Độc Lập Suy Nghĩ.
-
Giải Toán 12: Bài 1. Khái Niệm Số Phức
-
Lý Thuyết Hypebol Toán 10
-
Bài 37 Trang 109 SGK Hình Học 10 Nâng Cao, Tìm Tọa độ Các Tiêu ...