Bài 2.15 Trang 71 SBT Hình Học 11: Cho Hình Chóp S.ABCD Có đáy ...

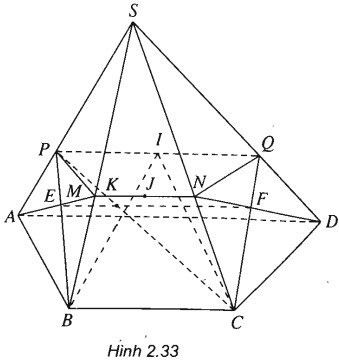
Cho hình chóp S.ABCD có đáy là hình thang ABCD với đáy là AD và BC. Biết AD = a, BC = b. Gọi I và J lần lượt là trọng tâm của các tam giác SAD và SBC. Mặt phẳng (ADJ) cắt SB, SC lần lượt tại M, N. Mặt phẳng (BCI) cắt SA, SD lần lượt tại P, Q.

a) Chứng minh MN song song với PQ.

b) Giả sử AM cắt BP tại E; CQ cắt DN tại F. Chứng minh rằng EF song song với MN và PQ. Tính EF theo a và b.

(h.2.33)

a)

Ta có: \(I \in \left( {SA{\rm{D}}} \right) \Rightarrow I \in \left( {SA{\rm{D}}} \right) \cap \left( {IBC} \right)\) 

Vậy

\(\left\{ \matrix{ A{\rm{D}}\parallel BC \hfill \cr A{\rm{D}} \subset \left( {SA{\rm{D}}} \right) \hfill \cr BC \subset \left( {IBC} \right) \hfill \cr} \right. \Rightarrow \left( {SA{\rm{D}}} \right) \cap \left( {IBC} \right) = PQ\)

và \(PQ\parallel A{\rm{D}}\parallel BC \,\,\,\,\,\,\,\,\,\,\left( 1 \right)\)

Tương tự: \(J \in \left( {SBC} \right) \Rightarrow J \in \left( {SBC} \right) \cap \left( {JAD} \right)\)

Vậy

\(\left\{ \matrix{ A{\rm{D}}\parallel BC \hfill \cr A{\rm{D}} \subset \left( {JA{\rm{D}}} \right) \hfill \cr BC \subset \left( {SBC} \right) \hfill \cr} \right. \Rightarrow \left( {JA{\rm{D}}} \right) \cap \left( {SBC} \right) = MN\) và \(MN\parallel BC\parallel AD\,\,\,\,\,\,\,\left( 2 \right)\)

Từ (1) và (2) suy ra \(PQ\parallel MN\).

Advertisements (Quảng cáo)

b) Ta có:

\(E = AM \cap BP \Rightarrow \left\{ \matrix{ E \in \left( {AMN{\rm{D}}} \right) \hfill \cr E \in \left( {PBCQ} \right) \hfill \cr} \right.\)

\(F = DN \cap CQ \Rightarrow \left\{ \matrix{ F \in \left( {AMN{\rm{D}}} \right) \hfill \cr F \in \left( {PBCQ} \right) \hfill \cr} \right.\)

Do đó: \(EF = \left( {AMN{\rm{D}}} \right) \cap \left( {PBCQ} \right)\)

Mà

\(\left\{ \matrix{ A{\rm{D}}\parallel BC \hfill \cr MN\parallel PQ \hfill \cr} \right.\) suy ra \(EF\parallel A{\rm{D}}\parallel BC\parallel MN\parallel PQ\)

Tính 

\(EF:CP \cap EF = K \Rightarrow EF = EK + KF\) 

\(EK\parallel BC \Rightarrow {{EK} \over {BC}} = {{PE} \over {PB}}\,\,\,\,\,\,\,\,\,\,\,\,\,\left( * \right)\)

\(PM\parallel AB \Rightarrow {{PE} \over {EB}} = {{PM} \over {AB}}\)

Mà \({{PM} \over {AB}} = {{SP} \over {SA}} = {2 \over 3}\) suy ra \({{PE} \over {EB}} = {2 \over 3}\)

Từ (*) suy ra

\(\eqalign{ & {{EK} \over {BC}} = {{PE} \over {PB}} = {{PE} \over {PE + EB}} \cr & = {1 \over {1 + {{EB} \over {PE}}}} = {1 \over {1 + {3 \over 2}}} = {2 \over 5} \cr & \Rightarrow EK = {2 \over 5}BC = {2 \over 5}b \cr} \)

Tương tự ta tính được \(KF = {2 \over 5}a\)

Vậy: \(EF = {2 \over 5}a + {2 \over 5}b = {2 \over 5}\left( {a + b} \right)\)