Bài 2. Giá Trị Lượng Giác Của Một Cung - SureTEST
Có thể bạn quan tâm
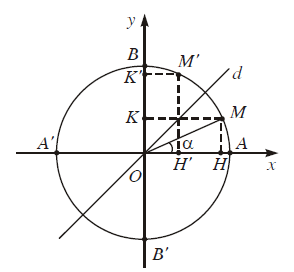
I. Giá trị của cung $\alpha $
1. Định nghĩa
Các giá trị sin$\alpha $, cos$\alpha $, tan$\alpha $, cot$\alpha $ được gọi là giá trị lượng giác của cung $\alpha $.
Ta cũng gọi trục tung là trục sin, còn trục hoành là trục côsin.
2. Hệ quả
Bảng xác định dấu của các giá trị lượng giác

3. Giá trị lượng giác của các cung đặc biệt

II. Ý nghĩa hình học của tan và cot
1. Ý nghĩa hình học của tan$\alpha $
tan$\alpha $ được biểu diễn bởi độ dài đại số của vectơ $\overrightarrow {AT} $ trên trục t’At.
Trục t’At được gọi là trục tan.

2. Ý nghĩa hình học của cot$\alpha $
cot$\alpha $ được biểu diễn bởi độ dài đại số của vectơ $\overrightarrow {BS} $ trên trục s’Bs. Trục s’Bs được gọi là trục cot.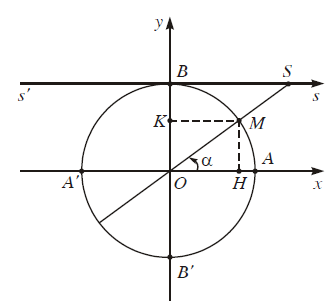
III. Quan hệ giữa các giá trị lượng giác
1. Công thức lượng giác cơ bản
$\begin{gathered} {\sin ^2}\alpha + {\cos ^2}\alpha = 1 \hfill \\ 1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }},\alpha \ne \frac{\pi }{2} + k\pi ,k \in Z \hfill \\ 1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }},\alpha \ne k\pi ,k \in Z \hfill \\ \tan \alpha .\cot \alpha = 1,\alpha \ne \frac{{k\pi }}{2},k \in Z \hfill \\ \end{gathered} $
2. Giá trị lượng giác của các cung có liên quan đặc biệt
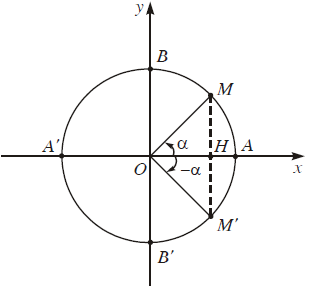
a) Cung đối nhau $\alpha $ và -$\alpha $
cos(-$\alpha $) = cos$\alpha $
sin(-$\alpha $) = -sin$\alpha $
tan(-$\alpha $) = -tan$\alpha $
cot(-$\alpha $) = -cot$\alpha $
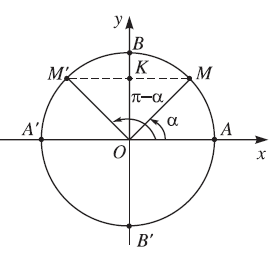
b) Cung bù nhau $\alpha $ và $\left( {\pi - \alpha } \right)$
$\begin{gathered} \sin \left( {\pi - \alpha } \right) = \sin \alpha \hfill \\ \cos \left( {\pi - \alpha } \right) = - \cos \alpha \hfill \\ \tan \left( {\pi - \alpha } \right) = - \tan \alpha \hfill \\ \cot \left( {\pi - \alpha } \right) = - \cot \alpha \hfill \\ \end{gathered} $
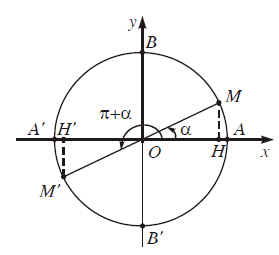
c) Cung hơn kém $\pi $: $\alpha $ và $\left( {\alpha + \pi } \right)$
$\begin{gathered} \sin \left( {\alpha + \pi } \right) = - \sin \alpha \hfill \\ \cos \left( {\alpha + \pi } \right) = - \cos \alpha \hfill \\ \tan \left( {\alpha + \pi } \right) = \tan \alpha \hfill \\ \cot \left( {\alpha + \pi } \right) = \cot \alpha \hfill \\ \end{gathered} $
d) Cung phụ nhau: $\alpha $ và $\left( {\frac{\pi }{2} - \alpha } \right)$
$\begin{gathered} \sin \left( {\frac{\pi }{2} - \alpha } \right) = \cos \alpha \hfill \\ \cos \left( {\frac{\pi }{2} - \alpha } \right) = \sin \alpha \hfill \\ \tan \left( {\frac{\pi }{2} - \alpha } \right) = \cot \alpha \hfill \\ \cot \left( {\frac{\pi }{2} - \alpha } \right) = \tan \alpha \hfill \\ \end{gathered} $
Từ khóa » Cung đối Nhau
-
Giá Trị Lượng Giác Của Các Góc (cung) Có Liên Quan đặc Biệt - Baitap123
-
Các Công Thức Lượng Giác Toán 10 Đầy Đủ Nhất - Kiến Guru
-
Giá Trị Lượng Giác Của Một Cung Và Những Hệ Quả - DINHNGHIA.VN
-
Các Cung Liên Kết đặc Biệt (2 Cung đối Nhau) - CungHocVui
-
Giá Trị Lượng Giác Của Một Cung, Lý Thuyết Và Bài Tập - Đại Số 10 ...
-
Giá Trị Lượng Giác Của Các Cung đối Nhau - Tài Liệu Text - 123doc
-
Hệ Thức Các Cung đặc Biệt A.Hai Cung đối Nhau: Các Cơng Thức ...
-
Giá Trị Lượng Giác Của Các Góc (cung) Có Liên Quan đặc Biệt
-
Giá Trị Lượng Giác Của Cung Có Liên Quan đặc Biệt - YouTube
-
Công Thức Lượng Giác - Giá Trị Lượng Giác Của Góc Lớp 10
-
Bảng Công Thức Lượng Giác đầy đủ,chi Tiết,dễ Hiểu - DeThiThu.Net
-
Cách Học Thuộc Nhanh Bảng Công Thức Lượng Giác Bằng Thơ, "thần ...
-
Tổng Hợp Cos đối, Sin Bù, Phụ Chéo ( Hai Góc đối Nhau, Bù Nhau ...