Bài 2. Phương Trình đường Tròn - Củng Cố Kiến Thức
Có thể bạn quan tâm
1. Phương trình đường tròn có tâm và bán kính cho trước
Trong mặt phẳng Oxy cho đường tròn (C) tâmI (a ; b), bán kính R. Ta có:
$\begin{gathered} M\left( {x;y} \right) \in \left( C \right) \Leftrightarrow IM = R \hfill \\ \Leftrightarrow \sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2}} = R \hfill \\ \Leftrightarrow {\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2} \hfill \\ \end{gathered} $

Phương trình ${\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}$ được gọi là phương trình đường tròn tâm I(a; b) bán kính R.
Chú ý
Phương trình đường tròn có tâm là gốc toạ độ O và có bán kính R là :
${x^2} + {y^2} = {R^2}$
2. Nhận xét
Phương trình đường tròn ${\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}$ có thể được viết dưới dạng ${x^2} + {y^2} - 2ax - 2by + c = 0$, trong đó $c = {a^2} + {b^2} - {R^2}$.
Ngược lại, phương trình ${x^2} + {y^2} - 2ax - 2by + c = 0$ là phương trình của đường tròn (C) khi và chỉ khi ${a^2} + {b^2} - c > 0$. Khi đó đường tròn (C) có tâm I(a ; b) và bán kính $R = \sqrt {{a^2} + {b^2} - c} $.
3. Phương trình tiếp tuyến của đường tròn
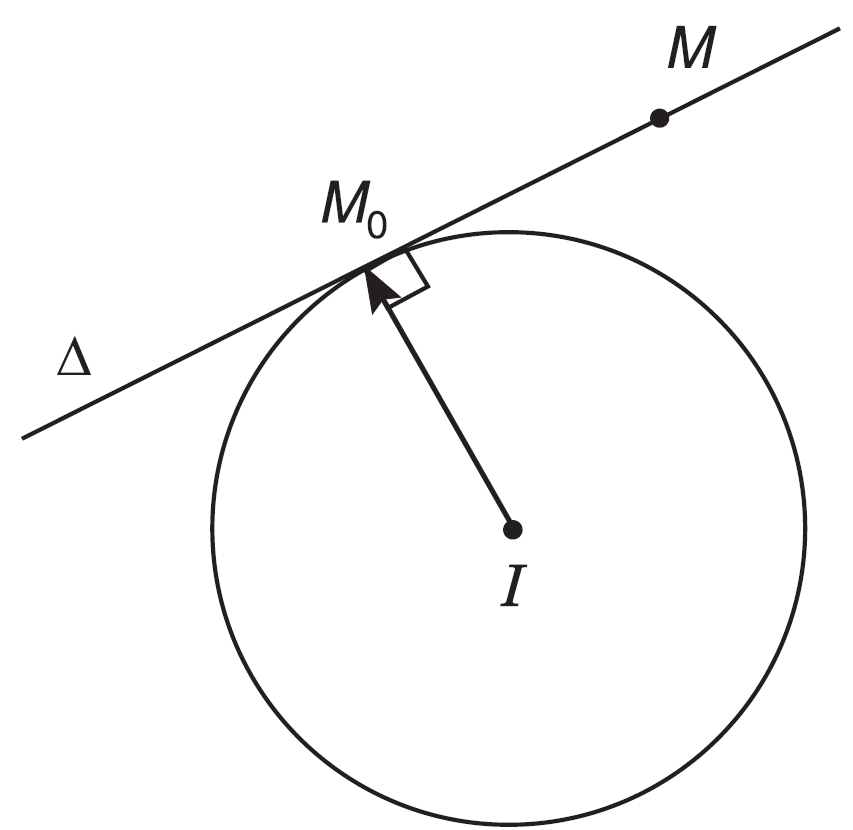
Cho điểm ${M_0}\left( {{x_0};{y_0}} \right)$nằm trên đường tròn (C) tâm I(a ; b). Gọi $\Delta $ là tiếp tuyến với (C) tại ${M_0}$.
Ta có ${M_0}$ thuộc $\Delta $ và vectơ $\overrightarrow {I{M_0}} = \left( {{x_0} - a;{y_0} - b} \right)$ là vectơ pháp tuyến của $\Delta $. Do đó $\Delta $ có phương trình là:
$\left( {{x_0} - a} \right)\left( {x - {x_0}} \right) + \left( {{y_0} - b} \right)\left( {y - {y_0}} \right) = 0$ (2)
Phương trình (2) là phương trình tiếp tuyến của đường tròn ${\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}$ tại điểm ${M_0}$ nằm trên đường tròn.
Từ khóa » Công Thức Tính Bán Kính Pt đường Tròn
-
Tìm Tọa độ Tâm Và Bán Kính Của đường Tròn
-
Lý Thuyết Phương Trình đường Tròn | SGK Toán Lớp 10
-
Tìm Tâm Và Bán Kính đường Tròn
-
Phương Trình đường Tròn: Lý Thuyết, Công Thức Và Cách Giải Các Dạng ...
-
Phương Trình đường Tròn: Lý Thuyết, Công Thức, Cách Giải Các Dạng ...
-
Cách để Tính Bán Kính Đường Tròn - WikiHow
-
Công Thức Phương Trình đường Tròn Và Bài Tập Có Lời Giải Chi Tiết
-
Công Thức Tính Bán Kính đường Tròn [dễ Nhớ] - Babelgraph
-
§2. Phương Trình đường Tròn - Hoc24
-
Chia Sẽ Phương Trình Và Công Thức đường Tròn đơn Giản
-
Phương Trình Của đường Tròn Là Gì ? Phương Trình Tổng Quát Có Tâm ...
-
Phương Trình đường Tròn Và Các Dạng Bài Tập Lớp 10, 12
-
Phương Trình đường Tròn Lớp 10 Chuẩn Nhất - CungHocVui
-
Viết Phương Trình đường Tròn Biết Tâm, Bán Kính, đường Kính