Bài 2. Quy Tắc Tính đạo Hàm - SureTEST

Trang chủ » đạo Hàm U(x)^v(x) » Bài 2. Quy Tắc Tính đạo Hàm - SureTEST

Có thể bạn quan tâm

I. Đạo hàm của số hàm số thường gặp

* Định lí 1

Hàm số $y = {x^n}\left( {x \in N,n > 1} \right)$ có đạo hàm tại mọi ${x \in R}$ và

$\left( {{x^n}} \right)' = n{x^{n - 1}}$.

* Định lí 2

Hàm số $y = \sqrt x $ có đạo hàm tại mọi x dương và

$\left( {\sqrt x } \right)' = \frac{1}{{2\sqrt x }}$.

II. Đạo hàm của tổng, hiệu, tích, thương

1. Định lí

* Định lí 3

Giả sử $u = u\left( x \right);v = v\left( x \right)$ là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Ta có:

$\begin{array}{l} \left( {u + v} \right)' = u' + v'(1)\\ \left( {u - v} \right)' = u' - v'(2)\\ \left( {uv} \right)' = u'v + v'u(3)\\ \left( {\frac{u}{v}} \right)' = \frac{{u' + v'}}{{{v^2}}}\left( {v = v\left( x \right) \ne 0} \right)(4) \end{array}$

2. Hệ quả

* Hệ quả 1

Nếu k là một hằng số thì $\left( {ku} \right)' = ku'$.

* Hệ quả 2

$\left( {\frac{1}{v}} \right)' = \frac{{v'}}{{{v^2}}}\left( {v = v\left( x \right) \ne 0} \right)$.

III. Đạo hàm của hàm hợp

1. Hàm hợp

Ta gọi hàm $y = f\left( {g\left( x \right)} \right)$ là hàm hợp của hàm $y = f\left( u \right)$ với $u = g\left( x \right)$.

2. Đạo hàm của hàm hợp

* Định lí 4

Nếu hàm số $u = g\left( x \right)$ có đạo hàm tại x là $u{'_x}$ và hàm số $y = f\left( u \right)$ có đạo hàm tại u là $y{'_u}$ thì hàm hợp $y = f\left( {g\left( x \right)} \right)$ có đạo hàm tại x là

$y{'_x} = y{'_u}.u{'_x}$.

Bảng tóm tắt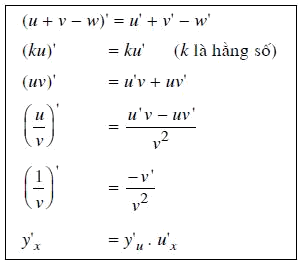

Từ khóa » đạo Hàm U(x)^v(x)