Bài 23 Trang 66 SGK Toán 7 Tập 2

Có thể bạn quan tâm

Đề bài

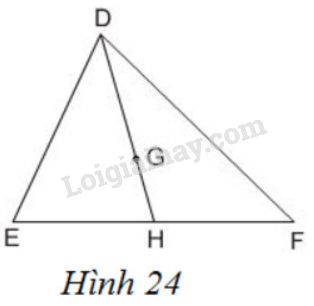
Cho \(G\) là trọng tâm của tam giác \(DEF\) với đường trung tuyến \(DH\). Trong các khẳng định sau đây, khẳng định nào đúng ?

\(\dfrac{DG}{DH}= \dfrac{1}{2}\); \(\dfrac{DG}{GH}= 3\)

\(\dfrac{GH}{DH}= \dfrac{1}{3}\); \(\dfrac{GH}{DG}= \dfrac{2}{3}\)

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Áp dụng: Ba đường trung tuyến của một tam giác cùng đi qua một điểm. Điểm ấy cách mỗi đỉnh một khoảng bằng \(\dfrac{2}{3}\) độ dài đường trung tuyến đi qua đỉnh ấy.

Lời giải chi tiết

\(G\) là trọng tâm của tam giác \(DEF\), đường trung tuyến \(DH\). Ta có:

\(\dfrac{{DG}}{{DH}} = \dfrac{2}{3}\) nên ta gọi \(DG = 2a;DH = 3a\left( {a > 0} \right)\)

\(\Rightarrow\) \(GH=DH-DG=3a-2a=a\)

Do đó:

\(\begin{array}{l}\dfrac{{DG}}{{GH}} = \dfrac{{2a}}{a} = 2;\dfrac{{GH}}{{DH}} = \dfrac{a}{{3a}} = \dfrac{1}{3};\\\dfrac{{GH}}{{DG}} = \dfrac{a}{{2a}} = \dfrac{1}{2}\end{array}\)

Vậy khẳng định \(\dfrac{GH}{DH}= \dfrac{1}{3}\) là đúng.

Các khẳng định còn lại sai.

Từ khóa » Toán Lớp 7 Tập 2 Bài 23 Trang 66

Bài 23 Trang 66 SGK Toán 7 Tập 2